-
1、如图，在平面直角坐标系中，正方形OABC 的顶点O 与原点重合，顶点 A，C 分别在x轴，y轴上，反比例函数 的图象与正方形的两边 AB，BC 分别交于点M，N，连接OM，ON，MN，若∠MON=45°，MN=2，则k 的值为.
-
2、如图，菱形 ABCD 的顶点 A 在函数 的图象上，函数 的图象关于直线 AC 对称，且经过 B，D 两点，若 AB =2，∠BAD=30°，则 k 的值为.
-
3、若反比例函数 与一次函数y=x+b的图象交于点A(m，n)，利用图象的对称性可知它们的另一个交点是( )A、(n，m) B、(-n，-m) C、(-m，-n) D、(-m，n)
-
4、仅用无刻度的直尺分别画出下列圆弧所在圆的圆心O.
(1)、在图1中，D是格点，E是网格线上的点，圆弧所在圆的直径为 DE；(2)、在图2中，圆弧经过格点 A，B，C. -
5、如图，P 为直线y=x+3上的一动点，过点 P 的直线 PE，PF 分别与抛物线 只有一个公共点，问直线 EF 是否经过定点?请说明理由.
-
6、如图，点 M，N 在抛物线 上，点 M 在点 N 的右边，若△MNE 的两条边ME，NE 所在的直线与抛物线都有唯一公共点，且S△MNE=2，设 M，N两点的横坐标分别为m，n，求m 与n的数量关系.
-
7、如图，抛物线 与x 轴交于A，B 两点(A 在B 的左侧)，与 y 轴交于点C，P 为y轴上C点下方的一动点，PM，PN 分别与抛物线交于唯一公共点M，N，连接MN交y轴于点Q，求 的值.
-
8、如图，直线AB 经过点C(0，1)，交抛物线 于A，B 两点，直线 PA，PB 都与抛物线只有唯一公共点.求证：直线 PA，PB 的交点P 在某条定直线上.
-
9、如图，E，F 是菱形ABCD 边AB，AD上的点，连接DE，点G 在DE 上，连接AG，FG，CG，∠AGD=∠BAD，AF=AE.
(1)、求证：△ADE∽△GDA；(2)、求证： -
10、如图，E，F，H 是正方形ABCD 边上的点，BE⊥CF，连接AG，GH，若CE=CH，求证：∠BAG=∠CHG.
-
11、如图，已知AB=AC，AD∥BC，CD⊥AC，连接BD 交AC 于点P，CH⊥AB 于点H.求证：
-
12、有一块矩形地块ABCD，AB=20m，BC=30m.为美观，拟种植不同的花卉，如图所示，将矩形ABCD 分割成四个等腰梯形及一个矩形，其中梯形的高相等，均为x 米.现决定在等腰梯形AEHD和 BCGF 中种植甲种花卉，在等腰梯形 ABFE 和 CDHG 中种植乙种花卉，在矩形 EFGH 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/m2 ， 60元/m2 ， 40元/m2 ， 设三种花卉的种植总成本为 y 元.
(1)、当x=5时，求种植总成本y；(2)、求种植总成本y 与x 的函数解析式，并写出自变量x的取值范围；(3)、若甲，乙两种花卉的种植面积之和不超过456 m2 ， 求三种花卉的最低种植总成本. -
13、某花圃基地计划将如图所示的一块长40 m，宽20 m的矩形空地划分成五块小矩形区域.其中一块正方形空地为育苗区，另一块空地为活动区，其余空地为种植区，分别种植A，B，C三种花卉.活动区一边与育苗区等宽，另一边长是10m. A，B，C三种花卉每平方米的产值分别是2百元、3百元、4百元.
(1)、设育苗区的边长为x m，用含x 的代数式表示下列各量：花卉A 的种植面积是 m2 ， 花卉 B 的种植面积是 花卉C 的种植面积是(2)、若花卉A 与B 的种植面积之和不超过560 m2 ， 求A，B，C三种花卉的总产值之和的最大值. -
14、仅用无刻度的直尺完成下列画图.
(1)、在图1中，经过格点A，B，C的圆与网格线交于点D.在上画点F，使得AF=AD；(2)、在图2中，经过格点A，B的圆与网格线交于点C，在.上画点P，使得 -
15、仅用无刻度的直尺完成下列画图.
(1)、在图1中，⊙O与网格线交于点A，B，C 是⊙O上的一点，在上画点E，使得(2)、在图2中，经过格点 A，B，C的圆与网格线交于点D，在BC上画点F，使得DF=DA. -
16、仅用无刻度的直尺完成下列画图.
(1)、在图1中，P是经过格点A，B的圆上一点，先画出该圆的圆心O，再在⊙O上画点H，使得∠APH=45°，画出所有符合条件的点 H；(2)、在图2中，O 是格点，在⊙O 上画一个15°的圆周角. -
17、如图，抛物线 交x 轴于A(-1，0)，B(3，0)两点，交 y 轴于点C(0，-3)，Q 为线段BC 上的动点.
(1)、直接写出抛物线的解析式；(2)、过点Q作PQ∥AC 交第四象限内的抛物线于点 P，连接 PA，PB，记△PAQ 与△PBQ面积分别为S1 ， S2 ， 设. 当 S 最大时，求点 P 的坐标，并求 S 的最大值. -
18、如图，抛物线 与x轴交于A(-4，0)，B(2，0)两点，与 y轴交于点C. P 为第三象限内抛物线上一点，作直线AC，连接PA，PC，求△PAC 面积的最大值及此时点P 的坐标.
-
19、如图，有一块五边形余料ABCDE，AB=AE=6，BC=5，∠A=∠B=90°，∠C=135°，∠E>90°.要在这 答案块余料中截取一块矩形材料，其中一条边在AE 上，并使所截矩形材料的面积S 尽可能大.
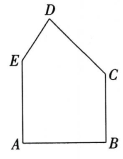(1)、若所截矩形材料的一条边是BC 或AE，求矩形材料的面积.(2)、能否截出比(1)中更大面积的矩形材料?如果能，求出能截取矩形材料面积的最大值；如果不能，请说明理由. -
20、在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB，BC两边).设AB=x m，花园的面积为S m2.
(1)、 若花园的面积为192m2 ， 求x 的值.(2)、写出S 与x之间的函数表达式.当x 为何值时，S有最大值?最大值为多少?(3)、若点 P 处有一棵树与墙CD，AD 的距离分别是a m(14≤a≤22)和6m ，要将这棵树围在花园内(含边界，不考虑树的粗细)，设S的最大值为y，求出 y 与a 之间的函数表达式.