沪科版数学七年级上册期末质量检测卷（四）

试卷更新日期：2025-11-13 类型：期末考试

进入出卷网下载

一、选择题（每题4分，共40分）

1. 若 $a = - {0.3}^{2}$ ， $b = - 3^{2}$ ， $c = {(- \frac{1}{3})}^{2}$ ， $d = {(- 3)}^{2}$ ，则（）

A、 $a < b < c < d$ B、 $b < a < c < d$ C、 $a < d < c < b$ D、 $c < a < d < b$

查看试题解析
2. 下列说法正确的是（）

A、若 $|a| = |b|$ ，则 $a = b$ B、若 $a < b$ ，则 $|a| < |b|$ C、若a、b互为相反数，则 $\frac{a}{b} = - 1$ D、若 $a > |b|$ ，则a＞b

查看试题解析
3. 中国信息通信研究院测算， $2020 \sim 2025$ 年，中国 $5G$ 商用带动的信息消费规模将超过8万亿元，直接带动经济总产出达 $10.6$ 万亿元．其中数据 $10.6$ 万亿用科学记数法表示为（）

A、 $10.6 \times 10^{4}$ B、 $1.06 \times 10^{13}$ C、 $10.6 \times 10^{13}$ D、 $1.06 \times 10^{8}$

查看试题解析
4. 方程3x-5=4x+8经移项得3x-4x=8+5，这实际上是在方程两边都加上（）

A、4x-5 B、4x+5 C、-4x-5 D、-4x+5

查看试题解析
5. 下列抽样调查中，样本选取最恰当的应是（）

A、一汽车苹果（约2.5万个），抽取了5个进行质量检测 B、一万块砖，抽出100块进行抗断检测 C、1000瓶可乐，存放了6个月后，现在要判断是否过期，抽出800瓶进行检测 D、一盒火柴（约100根），要检查它是否受潮，抽出85根进行试划

查看试题解析
6. 如图，点B，C，D在线段AE上，已知BD= $3, B D = \frac{1}{3} A E,$ 则图中所有线段的长度之和为 ( )

A、42 B、48 C、50 D、56

查看试题解析
7. 如果多项式 $(- a - 1) x^{5} - \frac{2}{3} x^{b} + x - 9$ 是关于 $x$ 的三次三项式，那么 $\frac{a}{b}$ 的值为（）

A、 $- 3$ B、 $- \frac{1}{3}$ C、 $3$ D、 $\frac{1}{3}$

查看试题解析
8. 文化情境·数学文化中国古代人民很早就在生产生活中发现了许多有趣的数学问题，其中《孙子算经》中有个问题：“今有三人共车，二车空；二人共车，九人步，问人与车各几何？”这道题的意思是：今有若干人乘车，每3人乘一车，最终剩余2辆车，若每2人共乘一车，最终剩余9个人无车可乘，问有多少人，多少辆车？如果我们设有 $x$ 辆车，则可列方程（）

A、 $3 (x - 2) = 2 x + 9$ B、 $3 (x + 2) = 2 x - 9$ C、 $\frac{x}{3} + 2 = \frac{x - 9}{2}$ D、 $\frac{x}{3} - 2 = \frac{x + 9}{2}$

查看试题解析
9. 如图， $∠ A O B = 120 °$ ，在 $∠ A O B$ 内作两条射线 $O C$ 和 $O D$ ，且 $O M$ 平分 $∠ A O D ， O N$ 平分 $∠ B O C$ ，若 $∠ A O C : ∠ C O D : ∠ D O B = 5 : 3 : 4$ ，则 $∠ M O N$ 的度数为（　　）

A、 $45 °$ B、 $50 °$ C、 $55 °$ D、 $60 °$

查看试题解析
10. 将正方形纸片 $B E F G$ 和正方形纸片 $D H M N$ 按如图所示放入周长为10的长方形 $A B C D$ 中，将图中的两个空白图形分别记为 $P ， Q$ ，已知下列某个选项的值，仍不能求出甲的周长，这个选项是（）

A、乙的周长 B、丙的周长 C、 $P$ 与 $Q$ 的周长和 D、 $P$ 与 $Q$ 的周长差

查看试题解析

二、填空题（每题4分，共32分）

11. 单项式 $- 3 x y^{2}$ 的次数是.

查看试题解析
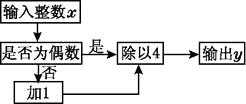
12. 计算： $52 ° 4 2^{'} + 37 ° 1 8^{'} =$ $°$ ．

查看试题解析
13. 用四舍五人法，把3.024596精确到百分位是

查看试题解析
14. 一商场对某款羊毛衫进行换季打折销售，若这款羊毛衫每件按原销售价的八折销售，售价为120元，则这款羊毛衫每件的原销售价为元.

查看试题解析
15. 定义：若点 $C$ 为直线 $A B$ 上的一点，且满足 $A C = 2 B C$ ，则称点 $C$ 是线段 $A B$ 的＂巧分点＂．现已知 $A B$ $= 6$ ，点 $C$ 是线段 $A B$ 的＂巧分点＂，则 $B C =$ ．

查看试题解析
16. 在如图所示的运算流程中，若输出的数y=7，则输入的数x=.

查看试题解析
17. 如图，已知长方形纸片 $A B C D$ ，点E在边 $A B$ 上，点F、G在边 $C D$ 上，连接 $E G$ 、 $E F$ ．将 $∠ B E G$ 对折，点B落在直线 $E G$ 上的点 $B^{'}$ 处，得折痕 $E M$ ；将 $∠ A E F$ 对折，点A落在直线 $E F$ 上的点 $A^{'}$ 处，得折痕 $E N$ ，若点G在点F的右侧，且 $∠ M E N = 102 °$ ．则 $∠ F E G$ 的度数为．

查看试题解析
18. 已知a，b为定值，若无论k为何值，关于x的方程 $\frac{k x - a}{3} = 1 - \frac{2 x + b k}{2}$ 的解总是x=2，则ab=.

查看试题解析

三、计算题（共8题，共78分）

19. 计算：

(1)、 $3 \frac{1}{2} - (- \frac{1}{3}) + 2 \frac{2}{3} + (- \frac{1}{2})$ .

(2)、 ${(- 3)}^{2} - (- 66) \times (\frac{1}{2} - \frac{1}{3} \times \frac{5}{11})$ .

查看试题解析
20. 计算： $\frac{4}{3} \times (- \frac{1}{6}) - \frac{5}{3} \div (- \frac{15}{7})$

查看试题解析
21. 解方程：

(1)、 $x - 3 = \frac{3}{2} x + 1$

(2)、 $\frac{3 y - 1}{4} - 1 = \frac{5 y - 7}{6}$

查看试题解析
22. 先化简，再求值： $3 x^{2} + 2 x y - 4 y^{2} - 2 (- 3 y^{2} + x y - x^{2})$ ，其中 $x = - 2$ ， $y = 1$ ．

查看试题解析
23. 某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷（每人必选且只能选一种），在全校范围内随机调查了部分学生，将统计结果绘制了如下两幅不完整的统计图：

请结合图中所给的信息解答下列问题：

(1)、这次统计中，喜欢用短信的有多少名学生？

(2)、通过计算，补全条形统计图；

(3)、该校共有2500名学生，请估计该校最喜欢用“微信”进行沟通的学生有多少名？

查看试题解析
24. OC平分∠AOB，OD 是∠BOC内部从点O 出发的一条射线，OE平分∠AOD。

(1)、【基础尝试】如图 2，若∠AOB=120°，∠COD=10°，求∠DOE的度数。

(2)、【画图探究】设 $∠ C O E = x °,$ 用x的代数式表示∠BOD 的度数。

(3)、【拓展运用】若∠COE 与∠BOD 互余，∠AOB 与∠COD 互补，求∠AOB 的度数。

查看试题解析
25. 综合实践
【素材】某商家促销电动车的方案为：A档电动车8折优惠，B档一次性降价600元．年底在原促销基础上再增加以下优惠：
新车原价
A档：2000元~3000元（含2000元，不含3000元）
B档：3000元及以上
减免
200元
300元
【问题】

(1)、若设原价为 $x$ 元，请用含 $x$ 的代数式填写实付价．
新车原价
A档：2000元~3000元（含2000元，不含3000元）
B档：3000元及以上
实付价
___________元
___________元

(2)、用2120元能购买到原价为多少元的电动车？

(3)、甲买了A档电动车，乙买了B档电动车，以下是他们的对话．
求甲、乙的实付价分别是多少元？

查看试题解析
26. 【背景知识】数轴是初中数学的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律：若数轴上点A、点B表示的数分别为a、b，则A，B两点之间的距离 $A B = | a - b |$ ，线段 $A B$ 的中点表示的数为 $\frac{a + b}{2}$ ．
【问题情境】如图，数轴上点A表示的数为 $- 2$ ，点B表示的数为8，点P从点A出发，以每秒3个单位长度的速度沿数轴向右匀速运动，同时点Q从点B出发，以每秒2个单位长度的速度向左匀速运动．设运动时间为t秒 $（ t > 0 ）$ ．
【综合运用】

(1)、填空：
①A、B两点间的距离 $A B =$ ，线段 $A B$ 的中点C表示的数为；
②用含t的代数式表示：t秒后，点P表示的数为；点Q表示的数为；

(2)、求当t为何值时， $P Q = \frac{1}{2} A B$ ；

(3)、若点M为 $P A$ 的中点，点N为 $P B$ 的中点，点P在运动过程中，线段 $M N$ 的长度是否发生变化？若变化，请说明理由；若不变，请求出线段 $M N$ 的长．

查看试题解析

新车原价	A档：2000元~3000元（含2000元，不含3000元）	B档：3000元及以上
减免	200元	300元

新车原价	A档：2000元~3000元（含2000元，不含3000元）	B档：3000元及以上
实付价	___________元	___________元