第七章 命题与证明提升卷一北师大版数学八(上)单元分层测
试卷更新日期：2025-11-12 类型：单元试卷
一、选择题（本大题共8小题, 每小题3分, 共24分, 每小题有四个选项, 其中只有一个是正确的）
-
1. 下列不是公理的是（ ）A、对顶角相等 B、两角及其夹边分别相等的两个三角形全等 C、同位角相等，两直线平行 D、三边分别相等的两个三角形全等2. 如图，直线l∥AB，∠A＝2∠B.若∠1＝108°，则∠2的度数为（ ）
A、36° B、46° C、72° D、82°3. 如图， ， 添加下列条件，还不能使成立的是（ ）
A、 B、 C、 D、4. 如图，直线a∥b，一个三角尺的直角顶点在直线a上，两直角边均与直线b相交，若∠1＝40°，则∠2＝（ ）
A、40° B、50° C、60° D、65°5. 如图，在中， ， ， ， 是边上的中线，过点C作的垂线交于点E，交于点F，连结 ． 若记为α，为β，则的度数为（ ）
A、 B、 C、 D、二、填空题（本大题共5小题, 每小题3分, 共15分）
-
6. 如图，AB∥CD，BC∥ED，∠B＝80°，则∠D＝.
三、解答题（共7题；共61分)
-
7. 如图，点E，F分别在AB，CD上，AF⊥CE于点O，∠1＝∠B，∠A＋∠2＝90°.求证：AB∥CD.请填空：
证明：∵AF⊥CE（已知），
∴∠AOE＝90°（）.
∵∠1＝∠B（），
∴（）.
∴∠AFB＝∠AOE（）.
∴∠AFB＝90°（）.
又∵∠AFC＋∠AFB＋∠2＝（平角的定义），
∴∠AFC＋∠2＝.
又∵∠A＋∠2＝90°（已知），
∴∠A＝∠AFC（）.
∴（内错角相等，两直线平行）.
8. 如图，在中，点D是边上一点，点E是边延长线上一点， ， 点F为外一点，连接 ， ， ， ， 求证： ．
9.
(1)、如图，DE∥BC，∠1=∠3，CD⊥AB，试说明FG⊥AB.(2)、若把(1)中的题设中的“DE∥BC”与结论“FG⊥AB”对调，所得命题是不是真命题?试说明理由.10. 我们定义：【概念理解】
在一个三角形中，如果一个角的度数是另一个角度数的 4 倍，那么这样的三角形我们称之为“完美三角形”．如：三个内角分别为 130°，40°，10°的三角形是“完美三角形”.
【简单应用】
如图 1，∠MON=72°，在射线OM上找一点A，过点A作AB⊥OM 交ON于点B，以A为端点作射线AD，交线段OB 于点C（点 C不与 O，B重合）
（1）∠ABO＝ ， △AOB__________（填“是”或“不是”）“完美三角形”；
（2）若∠ACB＝90°，求证：△AOC是“完美三角形”．
【应用拓展】
如图 2，点D在△ABC 的边AB上，连接DC，作∠ADC的平分线交AC于点E，在DC上取点F，使 ， ． 若△BCD是“完美三角形”， 求∠B的度数．
11. 【问题呈现】如图①，已知线段 ， 相交于点 ， 连结 ， ， 我们把形如这样的图形称为“字型”．
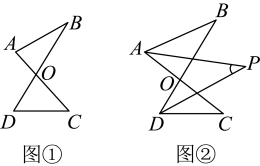(1)、证明： ．(2)、【问题探究】继续探究，如图②，、分别平分、 ， 、交于点 ， 求与、之间的数量关系．为了研究这一问题，尝试代入、的值求的值，得到下面几组对应值：
表中 ， 猜想得到与、的数量关系为；
(3)、证明（）中猜想得到的与、的数量关系；（单位：度）
（单位：度）
（单位：度）
-