第六章数据的分析培优卷一北师大版数学八(上)单元分层测

试卷更新日期：2025-11-12 类型：单元试卷

进入出卷网下载

一、选择题（本大题共8小题, 每小题3分, 共24分, 每小题有四个选项, 其中只有一个是正确的）

1. 某学校计划组织“垫排球”比赛活动，为了解参赛学生垫排球水平及稳定程度，在比赛前期分别记录了甲、乙、丙、丁四名参赛学生在规定时间内10次垫排球的数量，并计算出了各自的平均个数 $\bar{x}$ 及方差 $S^{2}$ ，如表所示：
参赛学生
甲
乙
丙
丁
$\bar{x}$
51
53
55
55
$S^{2}$
$\frac{23}{4}$
$\frac{21}{4}$
6
$\frac{21}{4}$
根据上表所列数据，你认为参赛学生中获胜的可能性最大的是（　　）

A、甲 B、乙 C、丙 D、丁

查看试题解析
2. 某滑雪俱乐部12名会员被分成甲、乙两组，他们的身高情况如图所示，甲组身高的平均数为 $\bar{x_{甲}} = 176 c m$ ，则下列结论正确的是（）

A、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $s_{甲}^{2} < s_{乙}^{2}$ B、 $\bar{x_{甲}} = \bar{x_{乙}}$ ， $s_{甲}^{2} > s_{乙}^{2}$ C、 $\bar{x_{甲}} < \bar{x_{乙}}$ ， $s_{甲}^{2} < s_{乙}^{2}$ D、 $\bar{x_{甲}} > \bar{x_{乙}}$ ， $s_{甲}^{2} > s_{乙}^{2}$

查看试题解析
3. 对于一组数据 3，3，2，3，6，3，10，3，6，3，2，下列结论正确的有（）．
①这组数据的众数是3；

②这组数据的众数与中位数的数值相等；

③这组数据的中位数与平均数的数值相等；

④这组数据的平均数与众数的数值相等．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 某公司要招聘一名职员，根据实际需要，从学历、经验、能力和态度四个方面对甲、乙、丙三名应聘者进行了测试，三名应聘者测试成绩如下表
项目
应聘者
甲
乙
丙
学历
9
8
8
经验
8
6
9
能力
7
8
8
态度
5
7
5
如果将学历、经验、能力和态度四项得分按 $2 ： 1 ： 2 ： 3$ 的比例确定每人的最终得分，并以此为依据确定录用者，那么（）将被录用

A、甲 B、乙 C、丙

查看试题解析
5. 某商店销售 $5$ 种领口大小分别为 $38$ ， $39$ ， $40$ ， $41$ ， $42 ($ 单位： $c m)$ 的衬衫，一个月内的销量如下表：
领口大小 $/ c m$
     $38$
     $39$
     $40$
     $41$
     $42$
销量 $/$ 件
     $64$
     $199$
     $180$
     $110$
     $47$
你认为商店最感兴趣的是这里数据的（）

A、平均数 B、中位数 C、众数 D、加权平均数

查看试题解析
6. 在第60届国际数学奥林匹克比赛中，中国队荣获团体总分第一名．我国参赛选手比赛成绩的方差计算公式为： $s^{2} = \frac{1}{6} [{(x_{1} - 38)}^{2} + {(x_{2} - 38)}^{2} + \dots + {(x_{6} - 38)}^{2}]$ ，下列说法错误的是（）．

A、我国一共派出了6名选手 B、我国参赛选手的平均成绩为38分 C、我国选手比赛成绩的中位数为38 D、我国选手比赛成绩的团体总分为228分

查看试题解析
7. 有甲、乙两种糖果，原价分别为每千克a元和b元，根据调查，将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合，取得了较好的销售效果，现在糖果价格有了调整：甲种糖果单价下降15%，乙种糖果单价上涨20%，但按原比例混合的糖果单价恰好不变，则 $\frac{x}{y}$ =（）

A、 $\frac{3 a}{4 b}$ B、 $\frac{4 a}{3 b}$ C、 $\frac{3 b}{4 a}$ D、 $\frac{4 b}{3 a}$

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分）

8. 在方差计算公式 $s^{2} = \frac{1}{20} [{(x_{1} - 15)}^{2} + {(x_{2} - 15)}^{2} + ⋯ + {(x_{20} - 15)}^{2}]$ 中，可以看出 $x_{1} + x_{2} + \dots x_{20}$ 的值为．

查看试题解析
9. 在一次数学测验中，甲班有 $a$ 个人，平均分是 $m$ 分，乙班有 $b$ 个人，平均分是 $n$ 分，则这两个班的总平均成绩为分．

查看试题解析
10. 现有两组数据：甲：12，14，16，18；乙：2023，2022，2020，2019，它们的方差分别记作 ${S_{甲}}^{2}$ ， ${S_{乙}}^{2}$ ，则 ${S_{甲}}^{2}$ ${S_{乙}}^{2}$ （用“>”“=”“<”）.

查看试题解析
11. 已知一组数据a₁ ， a₂ ， a₃ ， ……，a_n的方差为3，则另一组数a₁+1，a₂+1，a₃+1，……，a_n+1的方差为．

查看试题解析

三、解答题（共7题；共61分)

12. 三个小组(每组20人)答一道满分为4分的题目，得分情况如下：

(1)、请分别计算三个小组该题的平均得分和方差.

(2)、观察这三个小组的得分情况，小明发现，“柱子的高度”总是1，2，3，6，8，但是它们排列的顺序不同，导致了平均数和方差发生了变化.若将这些“柱子”重新排列，则如何排列能使平均数最大?如何排列能使方差最小?

(3)、如果用三个箱线图分别表示这三个小组的成绩，那么这三个箱线图有什么差异?

查看试题解析
13. 发生火灾时，逃生时间通常仅有几分钟，采取有效的自救与逃生措施能够显著降低人员伤亡。某中学针对八年级学生进行了逃生技能掌握情况的调查，随机抽取了1班和2班各10名学生进行问卷调查，分数越高表明学生掌握的逃生技能越好，根据调查结果绘制了相应的统计图。
数据分析结果详见下表：
班级
平均数/分
中位数/分
众数/分
方差
1班
8.1
x
9
2.09
2班
y
9
9
1.24
请根据以上信息，解答下列问题：

(1)、x= ， y=；

(2)、补全条形统计图；

(3)、小颖的得分是9分，其分数高于她所在班级半数同学的个人得分，则小颖在班（填“1”或“2”）；

(4)、在逃生技能的掌握方面，你认为哪个班级的学生表现更优异?请说明理由。

查看试题解析
14. 为帮助学生了解“预防新型冠状病毒”的有关知识，学校组织了一次线上知识培训，培训结束后进行测试．试题的满分为20分．为了解学生的成绩情况，从七、八年级学生中各随机抽取了20名学生的成绩进行了整理、描述和分析．下面给出了部分信息：
抽取的20名七年级学生成绩是：20，20，20，20，19，19，19，19，18，18，18，18，18，18，18，17，16，16，15，14．
抽取的40名学生成绩统计表
性别
七年级
八年级
平均分
18
18
众数
a
b
中位数
18
c
方差
2.7
2.7
根据以上信息，解答下列问题：

(1)、直接写出表中a，b，c的值：a＝， b＝， c＝．

(2)、在这次测试中，你认为是七年级学生成绩好，还是八年级学生成绩好？请说明理由．

(3)、若九年级随机抽取20名学生的成绩的方差为2.5，则年级成绩更稳定（填“七”或“八”或“九”）．

查看试题解析
15. 在学校组织的“文明出行”知识竞赛中，8（1）和8（2）班参赛人数相同，成绩分为A、B、C三个等级，其中相应等级的得分依次记为A级100分、B级90分、C级80分，其中8（2）班有2人达到A级，将两个班的成绩整理并绘制成如下的统计图．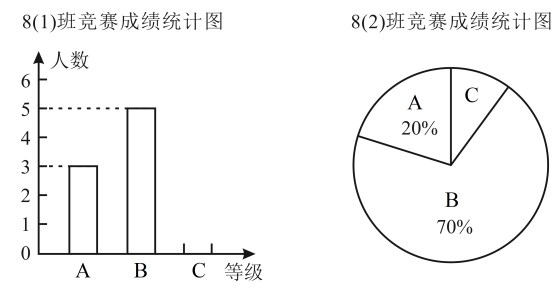
请解答下列问题：

(1)、求各班参赛人数，并补全条形统计图；

(2)、此次竞赛中8（2）班成绩的中位数a为分；

(3)、小明同学根据以上信息制作了如下统计表：

平均数（分）
中位数（分）
方差
8（1）班
m
90
n
8（2）班
91
a
29
请分别求出m和n的值，并从稳定性方面比较两个班的成绩．

查看试题解析
16. 某校八年级（1）班甲、乙两男生在5次引体向上测试中有效次数如下：
甲：8，8，7，8，9；乙：5，9，7，10，9；

甲乙两同学引体向上的平均数、众数、中位数、方差如下：

平均数

众数

中位数

方差

甲

8

b

8

0.4

乙

a

9

c

3.2

根据以上信息，回答下列问题：

(1)、表格是a＝， b＝， c＝.（填数值）

(2)、体育老师根据这5次的成绩，决定选择甲同学代表班级参加年级引体向上比赛，选择甲的理由是.班主任李老师根据去年比赛的成绩（至少9次才能获奖），决定选择乙同学代表班级参加年级引体向上比赛，选择乙的理由是；

(3)、如果乙同学再做一次引体向上，有效次数为8，那么乙同学6次引体向上成绩的平均数，中位数，方差.（填“变大”、“变小”或“不变”）

查看试题解析

参赛学生	甲	乙	丙	丁
$\bar{x}$	51	53	55	55
$S^{2}$	$\frac{23}{4}$	$\frac{21}{4}$	6	$\frac{21}{4}$

项目	应聘者
项目	甲	乙	丙
学历	9	8	8
经验	8	6	9
能力	7	8	8
态度	5	7	5

领口大小 $/ c m$	$38$	$39$	$40$	$41$	$42$
销量 $/$ 件	$64$	$199$	$180$	$110$	$47$

班级	平均数/分	中位数/分	众数/分	方差
1班	8.1	x	9	2.09
2班	y	9	9	1.24

性别	七年级	八年级
平均分	18	18
众数	a	b
中位数	18	c
方差	2.7	2.7

	平均数（分）	中位数（分）	方差
8（1）班	m	90	n
8（2）班	91	a	29

第六章 数据的分析培优卷一北师大版数学八(上)单元分层测

一、选择题（本大题共8小题, 每小题3分, 共24分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分）

三、解答题（共7题；共61分)

第六章数据的分析培优卷一北师大版数学八(上)单元分层测