-
1、分式方程的解为 ．
-
2、若二元一次方程组的解为 ， 则a+b的值为 ．
-
3、小明家1～5月的电费（单位：元）分别为：137，140，140，117，104．该组数据的中位数是 ．
-
4、2025年“五一”假期，约有166200人次的参观者走进淮塔园林接受红色教育．将166200用科学记数法表示为 ．
-
5、如图为一次函数y＝kx+b的图象，关于x的不等式k（x﹣3）+b＜0的解集为（ ）
A、x＜﹣4 B、x＞﹣4 C、x＜2 D、x＞2 -
6、如图为一个正方体的展开图，将其折成一个正方体，所得图形可能是（ ）
A、
B、
C、
D、
-
7、下列计算错误的是（ ）A、 B、 C、 D、
-
8、一只不透明的袋子中装有4个红球与2个黑球，每个球除颜色外都相同．从中任意摸出3个球，下列事件为必然事件的是（ ）A、至多有1个球是红球 B、至多有1个球是黑球 C、至少有1个球是红球 D、至少有1个球是黑球
-
9、传统纹样作为中华传统文化的一部分，具有深厚的底蕴．徐州出土汉代玉器的下列纹样，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
-
10、定义：在一个图形上画一条直线，若这条直线既平分该图形的面积，又平分该图形的周长，我们称这条直线为这个图形的“等分积周线”.
(1)、如图（1），已知△ABC，AC≠BC，过点 C 能否画出△ABC的一条“等分积周线”?若能，说出确定的方法；若不能，请说明理由.(2)、如图（2），在四边形ABCD 中，∠B=∠C=90°，EF垂直平分AD，垂足为 F，交 BC 于点 E，已知AB=3，BC=8，CD=5.试说明：直线 EF 为四边形ABCD 的“等分积周线”. -
11、如图，某沿海城市A 接到台风预警，在该市正南方向340 km的B 处有一台风中心，沿 BC 方向以 15 km/h 的速度移动，已知城市A 到 BC 的距离AD 为160 km.
(1)、台风中心经过多长时间从 B 点移到 D 点?(2)、如果在距台风中心200km的圆形区域内都将受到台风的影响，那么A 市受到台风影响的时间持续多少小时? -
12、在△ABC 中，AB=15，AC=20，D 是 BC 边所在直线上的点，AD=12，BD=9，则BC=.
-
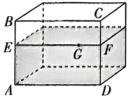
13、如图所示的长方体透明玻璃鱼缸，假设其长AD=80 cm，高AB=60 cm，水深AE=40 cm.在水面上紧贴内壁G处有一块面包屑，G在水面线EF上，且EG=60 cm，一只蚂蚁想从鱼缸外的A 点沿鱼缸壁爬进鱼缸内的G处吃面包屑，则蚂蚁爬行的最短路线长为cm.
-
14、如图，将直角三角形纸片ABC 沿AD 折叠，使点 B 落在AC 延长线上的点E处.若AC=3，BC=4，则图中阴影部分的面积是（ )
A、 B、 C、 D、 -
15、如图，小明将一张长为20cm，宽为15 cm的长方形纸片（AE>DE)剪去了一角，量得AB=6 cm，CD=8 cm，则 BC 的长为（ )
A、8cm B、13 cm C、15 cm D、20cm -
16、如图，所有四边形都是正方形，所有三角形都是直角三角形，若正方形A，B，C的面积依次为2，6，3，则正方形D的面积为（ )
A、6 B、8 C、11 D、12 -
17、某兴趣小组开展课外活动.如图，小明从点 M 出发以1.5m/s的速度，沿射线MN 方向匀速前进，2s后到达点B，此时他(AB)在某一灯光下的影长为MB，继续按原速行走2s到达点 D，此时他(CD)在同一灯光下的影子GD 仍落在其身后，并测得这个影长GD 为1.2m，然后他将速度提高到原来的1.5倍，再行走2s到达点F，此时A，C，E 三点共线.
(1)、请在图中画出点光源O 的位置，并画出小明位于点 F 时在这个灯光下的影长FH(不写画法).(2)、求小明到达点 F 时的影长FH. -
18、几何体的三视图相互关联.某直三棱柱的三视图如图所示，在 中，
(1)、 求 BC 及FG 的长.(2)、 若主视图(矩形ABCD)与左视图(矩形 EFGH)相似，求AB 的长.(3)、在(2)的条件下，求直三棱柱的全面积. -
19、如图①，某种冰激凌的外包装可以视为圆锥，它的底面圆直径ED 与母线AD 长之比为1：2.制作这种外包装需要用如图②所示的等腰三角形材料，其中 将扇形AEF 围成圆锥时，AE，AF 恰好重合.
(1)、求这种材料中∠BAC 的度数.(2)、若圆锥底面圆的直径ED 为5cm，求材料剩余部分(图中涂色部分)的面积(结果保留π). -
20、一个圆柱形零件，削去了占底面圆的四分之一部分的柱体(如图)，现已画出了其主视图与俯视图.
(1)、请只用直尺和圆规，画出此零件的左视图(不必写作法，保留作图痕迹).(2)、若此零件的高h=3cm，且其俯视图的弧长为3πcm，求此零件的表面积.