-
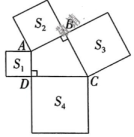
1、如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形 ABCD的四条边为边长,向外作四个正方形,面积分别为S1 , S2 , S3 , S4 , 若 则
-
2、如图,在△ABC 中,AB=AC=5,BC=6,则AC边上的高BD的长为( )
 A、4 B、4.4 C、4.8 D、5
A、4 B、4.4 C、4.8 D、5 -
3、如图,在Rt△ABC 中,∠ACB=90°,△ABC 的面积为24cm2 , 在AB 同侧分别以AB,BC,AC 为直径作三个半圆,则阴影部分的面积为cm2.

-
4、如图,AD 是△ABC 的高,分别以AB,BD,DC,CA 为边向外作正方形,其中3个正方形的面积如图所示,则第四个正方形的面积为 ( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
5、如图,在△ABC中,CD⊥AB 于点 D,E 在 AD 上,连接 CE,AE=CE.若AD=6,BC=5,BD=3,则DE的长为.

-
6、如图,Rt△ABC的顶点A,B 都在由边长为1 的小正方形组成的方格纸的格点上,且∠C=90°,则AB的长为.

-
7、如图,直线 AB⊥CD,垂足为 O,AO=15,CO=8,以点A 为圆心,AC 的长为半径画弧,交直线AB 于点 E,则OE 的长为( )
 A、8 B、6 C、4 D、2
A、8 B、6 C、4 D、2 -
8、在△ABC中,若∠ABC=90°,则下列正确的是 ( )A、BC=AB+AC B、 C、 D、
-
9、一辆装满货物的卡车,高2.5cm,宽1.6m,要开进上边是半圆,下边是长方形的隧道,如图所示,已知半圆的直径为2m,长方形的另一条边长是2.3m .
 (1)、此卡车是否能通过隧道?试说明你的理由.(2)、为了适应车流量的增加,现把隧道改为双行道,要使宽为1.2m,高为2.8 m的卡车能安全通过,那么此隧道的宽至少增加到多少?
(1)、此卡车是否能通过隧道?试说明你的理由.(2)、为了适应车流量的增加,现把隧道改为双行道,要使宽为1.2m,高为2.8 m的卡车能安全通过,那么此隧道的宽至少增加到多少? -
10、如图,在笔直的公路AB旁有一个城市书房 C,C 到公路AB 的距离 CD为80米,AC 为100米,BC 为300 米.一辆公交车以10米/秒的速度从A 处出发,沿公路AB向B 处行驶.若公交车鸣笛声会使以公交车为中心170米范围内受到噪音影响,则公交车在公路AB上行驶时,至少秒不鸣笛才能使在城市书房C 中看书的读者不受噪音影响.

-
11、小亮用11块高度都是2cm 的相同长方体小木块垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个正方形木板ABCD,截面如图所示.两木墙的高度分别为 AE 与 CF 的长,点B在 EF 上,则正方形木板 ABCD 的面积为cm2.

-
12、在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?意思是有一根竹子原高1丈(1丈=10尺),中间有一处折断,竹梢触地面处离竹根3尺(1尺 米),试问折断处离地面 ( )
 A、4尺 B、3.6尺 C、4.5尺 D、4.55尺
A、4尺 B、3.6尺 C、4.5尺 D、4.55尺 -
13、为验证勾股定理,小明进行了如下的思考:如图,在 Rt△ABC 中,∠ACB=90°,在边AC上截取 CE=CB,延长BC 到点 D,使得 CD=CA,连接AD,DE,并延长DE交AB 于点F,已知BC=a,AC=b,AB=c.
 (1)、在验证之前小明发现AB 和DE存在着一定的数量关系和位置关系,猜想 AB 和 DE 的数量关系和位置关系,并说明理由;(2)、通过以上条件验证勾股定理.
(1)、在验证之前小明发现AB 和DE存在着一定的数量关系和位置关系,猜想 AB 和 DE 的数量关系和位置关系,并说明理由;(2)、通过以上条件验证勾股定理. -
14、利用下列图形,能验证勾股定理的有 ( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
15、已知△ABC中,∠A=x°.
 (1)、如图(1),BO,CO 分别是∠ABC,∠ACB的平分线,则∠BOC=°(用含x 的代数式表示).(2)、如图(2),若∠ABC 和∠ACB 的三 等 分线 相交 于 点 O1 , O2 , 则 °.(用含x的代数式表示)(3)、如图(3),若∠ABC 和∠ACB的n等分线相交 于 点 O1 , O2 , …, On-1 , 则 ∠BO1C =°.(用含x及n的代数式表示)
(1)、如图(1),BO,CO 分别是∠ABC,∠ACB的平分线,则∠BOC=°(用含x 的代数式表示).(2)、如图(2),若∠ABC 和∠ACB 的三 等 分线 相交 于 点 O1 , O2 , 则 °.(用含x的代数式表示)(3)、如图(3),若∠ABC 和∠ACB的n等分线相交 于 点 O1 , O2 , …, On-1 , 则 ∠BO1C =°.(用含x及n的代数式表示) -
16、根据所给材料回答问题.
研究任务
画出平分三角形面积的一条直线
研究成果
中线法
分割法
BD 是 AC 边上的中线

若 直线 EF 平分△ABC的面积,则

成果应用
如图,在△ABC中,BD是AC边上的中线,直线 EF 平分△ABC的面积,交 BD 于点O.已知 , △ABC 的面积为10,则 , 四边形 BCFO 的面积为.

-
17、如图,在△ABC 中,∠A=60°,∠ACB=42°,D为边BC 延长线上的一点,BF平分∠ABC,E 为射线BF上一点.若直线 CE 垂直于△ABC 的一边,则∠BEC 的度数为.

-
18、如图,△ABC 的面积是15,AB=AC=6,O是边BC上任意一点(不与点B,C重合),OD⊥AB于点D,OE⊥AC 于点 E,设OD=a,OE=b,则代数式a+b的值是.

-
19、如图,在△ABC中,∠BAC=90°,AD 是高,BE 是中线,CF 是角平分线,CF 交AD 于点 G,交 BE 于点H,下面说法正确的是( )

①△ABE 与△BCE 的面积相等;②∠AFG=∠AGF;③∠FAG=2∠ACF.
A、①② B、①②③ C、②③ D、①③ -
20、如图,在△ABC中,若 CD,BE 是△ABC 的两条中线,则△ABC的周长是( )
 A、22 B、26 C、35 D、45
A、22 B、26 C、35 D、45