-
1、已知直线的图象经过点 , , 则关于的方程的解为( )A、 B、 C、 D、
-
2、已知一次函数和一次函数的自变量x与因变量 , 的部分对应数值如表所示,则关于x , y的二元一次方程组的解为( )
x
…
0
1
2
…
…
1
2
4
…
…
1
3
…
A、 B、 C、 D、 -
3、如图,一次函数的图象经过点 , 且与正比例函数的图象交于点 , 则这个一次函数的表达式是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
4、函数与的图象在同一直角坐标系中,位置关系是( )A、相交 B、互相垂直 C、平行 D、无法确定
-
5、如图,一次函数y=kx+b与正比例函数y=2x的图象交于点A , 则关于x , y的方程组的解为
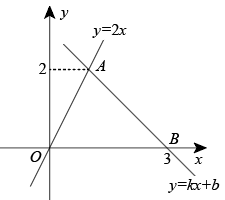 A、 B、 C、 D、
A、 B、 C、 D、 -
6、一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度返回甲地,货车到达乙地后停止,货车、轿车离甲地的距离(千米)与轿车所用时间(小时)的关系如图所示,则下列结论错误的是( ).
 A、甲、乙两地相距90千米 B、轿车返回的速度为每小时90千米 C、两车在出发小时后相遇 D、货车到达乙地时,轿车离乙地18千米
A、甲、乙两地相距90千米 B、轿车返回的速度为每小时90千米 C、两车在出发小时后相遇 D、货车到达乙地时,轿车离乙地18千米 -
7、已知4个正比例函数 , , , 的图像如图,则下列结论成立的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、 综合与实践
【问题情境】
在数学综合与实践活动课上,老师让同学们以“特殊平行四边形的旋转”为主题开展探究活动.
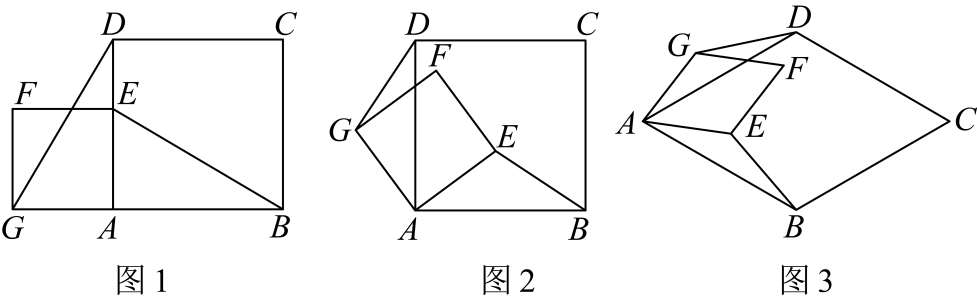
如图 , 正方形和正方形 , 连接 , .
(1)、【操作发现】当正方形绕点旋转,如图 , 线段与之间的数量关系是;直线与的夹角度数为;
(2)、【深入探究】如图 , 若四边形与四边形都为菱形,且 , , 猜想与的数量关系与直线与的夹角度数,并说明理由;
(3)、【迁移探究】如图 , 在(2)的条件下, , 在菱形绕点旋转过程中,直接写出线段的最小值.
-
9、 某公司销售一种商品,成本为每件30元,经过市场调查发现,该商品的每天销售数量y(件)与销售单价x(元)之间满足一次函数关系,部分数据如下表所示:
销售单价x/元
…
40
60
80
…
每天销售数量y/件
…
80
60
40
…
(1)、直接写出y与x之间的函数关系式;(2)、设该公司销售这种商品每天获利w(元),当销售单价为多少元时,每天获利最大?最大利润是多少元? -
10、 如图, , 交于点C , D , 是半径,且于点F .
 (1)、求证: .(2)、若 , , 求直径的长.
(1)、求证: .(2)、若 , , 求直径的长. -
11、 如图,每个小方格都是边长为1个单位长度的正方形,△ABC的三个顶点都在格点上(每个小方格的顶点叫格点).
 (1)、画出△ABC向上平移4个单位长度后得到的△A1B1C1;(2)、画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2 .
(1)、画出△ABC向上平移4个单位长度后得到的△A1B1C1;(2)、画出△ABC绕点O逆时针旋转90°后得到的△A2B2C2 . -
12、 已知抛物线经过点 .(1)、求此抛物线的函数表达式;(2)、判断点是否在此抛物线上.
-
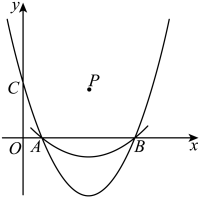
13、 如图,二次函数的图象交x轴于A , B两点,交y轴于点C , (P在第一象限)恰好经过A、B、C三点,且的弦心距为 , 则a的值为 .
-
14、 如图,把抛物线平移得到抛物线 , 抛物线经过点和原点,它的顶点为 , 它的对称轴与抛物线交于点 , 则图中阴影部分的面积为 .

-
15、 二次函数 , 当时,随的增大而 .
-
16、 一个圆的半径为 , 则此圆的最大弦长为 .
-
17、 二次函数的图象的开口向 .
-
18、 如图,已知点A , C , D在上,点B在内,和均为直角, , , , 则的半径为( )
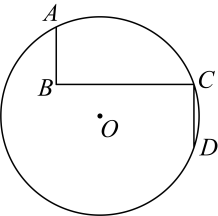 A、5 B、 C、 D、
A、5 B、 C、 D、 -
19、 二次函数的图象如图所示,其对称轴为直线 , 与x轴的一个交点为 . 则下列结论:①;②;③;④方程的两根为 , . 其中正确的结论是( )
 A、①②③ B、①③④ C、②③④ D、①②④
A、①②③ B、①③④ C、②③④ D、①②④ -
20、 如图,在边长为的正方形中,动点P从点A出发沿A→B的方向以1 cm/s的速度运动;同时,动点Q从点D出发沿D→C→B的方向以的速度运动.当点Q到达点B时,点P , Q同时停止运动.设的面积为y(),运动时间为x(),下列能大致反映y与x之间函数关系的图象是( )
 A、
A、 B、
B、 C、
C、 D、
D、