相关试卷

1、（1）若 $x, y$ 都是实数，且 $y = \sqrt{x - 3} + \sqrt{3 - x} + 8$ ，求 $5 x + 13 y + 6$ 的立方根；
（2）已知 $\sqrt[3]{3 y - 1}$ 与 $\sqrt[3]{1 - 2 x}$ 互为相反数，求 $\frac{x}{y}$ 的值．

查看解析
2、先化简，再求值： $[{(5 m - n)}^{2} - (5 m + n) (5 m - n)] \div 2 n$ ，其中 $m = - \frac{1}{5}$ ， $n = 2024$ ．

查看解析
3、利用乘法公式计算下列各题：

(1)、 $102 \times 98$ ；

(2)、 ${1.234}^{2} + {0.766}^{2} + 2.468 \times 0.766$ ．

查看解析
4、因式分解：

(1)、 $3 m^{2} + 6 m$ ；

(2)、 $x y^{3} - x y$ ；

(3)、 $(x - 1) (x - 3) + 1$ ．

查看解析
5、计算：

(1)、 ${(- 1)}^{2024} - \sqrt[3]{8} + \sqrt{4}$ ；

(2)、 $a^{2} \cdot a^{4} + {(- 2 a^{2})}^{3} + a^{8} \div a^{2}$ ．

查看解析
6、如果 $(a - 2) \sqrt{2} + b + 3 = 0$ ．其中 $a 、 b$ 为有理数，则 $a + 2 b =$ ．

查看解析
7、我国南宋时期杰出的数学家杨辉是钱塘人，下面的图表是他在《详解九章算法》中记载的“杨辉三角”．此图揭示了(a+b)ⁿ(n为非负整数)的展开式的项数及各项系数的有关规律．由此规律可解决如下问题：假如今天是星期三，再过7天还是星期三，那么再过8²¹天是( )

A、星期二 B、星期三 C、星期四 D、星期五

查看解析
8、若实数 $x$ ， $y$ 满足 $(x^{2} + y^{2}) (x^{2} + y^{2} - 4) = 5$ ，则 $x^{2} + y^{2}$ 的值为（）

A、5或 $- 1$ B、5 C、1或 $- 5$ D、1

查看解析
9、如图，把两个边长为 $1$ 的小正方形分别沿它的对角线剪开，将所得的 $4$ 个等腰直角三角形拼在一起，得到一个大正方形，则这个大正方形的边长为( )

A、 $1$ B、 $1.5$ C、 $\sqrt{2}$ D、 $2$

查看解析
10、下列叙述错误的是（）

A、平行四边形的对角线互相平分 B、矩形的对角线相等 C、菱形的对角线互相垂直 D、对角线相等的四边形是平行四边形

查看解析
11、如图，某跳水运动员进行10米跳台跳水训练，水面边缘点C的坐标为 $(- \frac{3}{2}, - 10)$ ．运动员（将运动员看成一点）在空中运动的路线是经过原点O的抛物线．在跳某个规定动作时，运动员在空中最高处A点的坐标为 $(1, \frac{5}{4})$ ，正常情况下，运动员在距水面高度5米以前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误．

(1)、求运动员在空中运动时对应抛物线的解析式并求出入水处B点的坐标；

(2)、若运动员在空中调整好入水姿势时，恰好距点C的水平距离为5米，问该运动员此次跳水会不会失误？通过计算说明理由．

查看解析
12、若 $x = 1$ 是一元二次方程 $x^{2} - 2 m x + 3 = 0$ 的解，则 $m$ 的值为（）

A、 $- 1$ B、 $0$ C、 $1$ D、 $2$

查看解析
13、下列方程中，是一元二次方程的是（）

A、 $x - 2 = 0$ B、 $x^{3} + 1 = 0$ C、 $x^{2} - 6 x - 8 = 0$ D、 $\frac{1}{x} = 6$

查看解析
14、某店销售一批户外帐篷，经调查，每顶帐篷利润为200元时，平均每天可售出60顶；单价每降价10元，每天可多售出4顶．已知该店要想平均每天盈利12160元，可列方程为 $(200 - x) (60 + \frac{x}{10} \times 4) = 12160$ ，则下列表述正确的是（）

A、每顶帐篷单价为x元 B、降价后平均每天可出售 $(200 - x)$ 顶 C、每顶帐篷单价应降价x元 D、降价后每顶帐篷利润为 $(60 + \frac{x}{10} \times 4)$ 元

查看解析
15、如图，是一个 $3 \times 3$ 的正方形网格，则 $∠ 1 + ∠ 2 + ∠ 3 + ∠ 4 =$ ．

查看解析
16、已知数轴上两点M、N对应的数分别为 $- 8$ 、4，点P为数轴上任意一点，其对应的数为x，

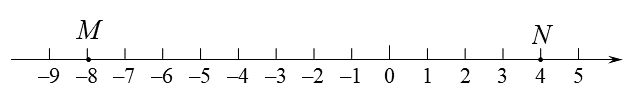(1)、一般地，数轴上表示数m和数n的两点之间的距离等于 $|m - n|$ ．则 $M N$ 的长为；

(2)、利用绝对值的几何意义，探索 $|x + 8| + |x - 4|$ 的最小值为；当 $x =$ 时， $|x + 8| + |x + 3| + |x - 4|$ 的值最小为；当 $|x + 3| + |x - m| + |x - 4|$ （m为整数）取得最小值时， $m =$ ；设 $a = |x + 1|$ ， $b = |x - 4|$ ， $c = |x + 8|$ ，则 $a + 2 b + c$ 的最小值为．

(3)、动点P从原点O点出发，以每秒5个单位长度的速度沿数轴向右匀速运动，设运动时间为 $t (t > 0)$ 秒．求当t为多少秒时？N，P两点之间的距离为2；

(4)、数轴上是否存在点P，使点P到点M、点N的距离之和是20？若存在，求出x的值；若不存在，请说明理由；（写出必要解答过程）

查看解析
17、观察下面三行数：
2， $- 4$ ， $8$ ， $- 16$ ， $32$ ， $- 64$ ， $\dots$ ①
$0$ ， $- 6$ ， $6$ ， $- 18$ ， $30$ ， $- 66$ ， $\dots$ ②
2、 $- 10$ 、14、 $- 34$ 、62、 $- 130$ ， $\dots$ ③

(1)、第①行第8个数是；第n个数是；

(2)、分别说出第②行第8个数是；和第③行第8个数是；

(3)、第1列的3个数之和为4，第二列3个数之和为 $- 20$ ，是否存在一列数3数之和为1020？若存在，说明是哪三个数；若不存在，说明理由．

查看解析
18、内江市为了节约用水，对自来水的收费标准作如下规定：每月每户用水量不超过6吨的部分，按2元/吨收费；超过6吨的部分按4元/吨收费．（水费按月份结算）

(1)、填空：若李华家3月份用水7吨，应交水费元？

(2)、若李华家4月份用水a吨（其中 $a > 6$ ），则应收水费多少元？（用含a的代数式表示，并化简）

(3)、若李华家4、5两个月共用水16吨（5月份用水量超过了4月份），设4月份用水x吨，求李华家4、5两个月共交水费多少元．（用含x代数式表示，并化简）

查看解析
19、观察下列各式，解答问题：
$1 - \frac{1}{2^{2}} = 1 - \frac{1}{4} = \frac{3}{4} = \frac{1}{2} \times \frac{3}{2}$ ；
$1 - \frac{1}{3^{2}} = 1 - \frac{1}{9} = \frac{8}{9} = \frac{2}{3} \times \frac{4}{3}$ ；
$1 - \frac{1}{4^{2}} = 1 - \frac{1}{16} = \frac{15}{16} = \frac{3}{4} \times \frac{5}{4}$ ；
$1 - \frac{1}{5^{2}} = 1 - \frac{1}{25} = \frac{24}{25} = \frac{4}{5} \times \frac{6}{5}$ ．
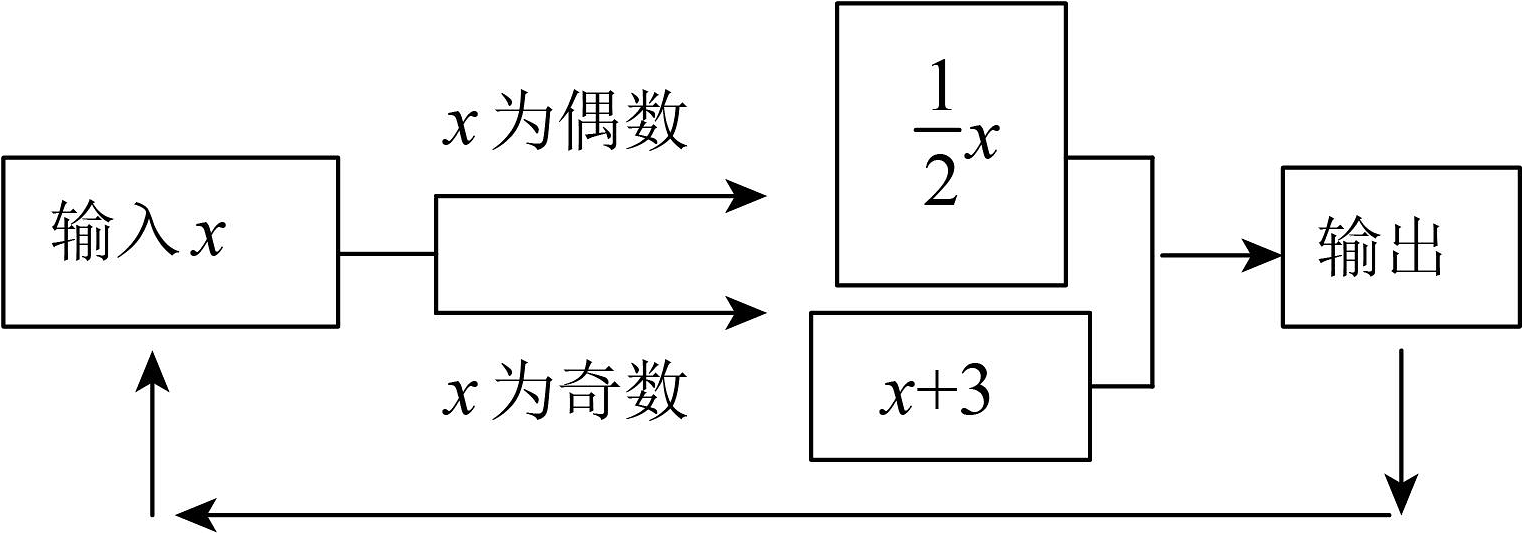
用你发现的规律计算： $(1 - \frac{1}{2^{2}}) \times (1 - \frac{1}{3^{2}}) \times (1 - \frac{1}{4^{2}}) \times \dots \times (1 - \frac{1}{2020^{2}}) \times (1 - \frac{1}{2021^{2}}) =$ ．

查看解析
20、如图所示的运算程序中，若开始输入的 $x$ 值为48，我们发现第1次输出的结果为24，第2次输出的结果为12，……第2017次输出的结果为．

查看解析

上一页 722 723 724 725 726 下一页跳转