人教版数学八年级上学期期末仿真模拟试卷二
试卷更新日期:2025-11-19 类型:期末考试
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. “二十四节气”是中国人通过观察太阳周年运动,认知一年中时令、气候、物候等变化规律所形成的知识体系和社会实践,下面四幅作品分别代表二十四节气中的“立春”“芒种”“白露”“大雪”,其中是轴对称图形的是 ( )A、
 B、
B、 C、
C、 D、
D、 2. 科幻作品《三体》一书中,三体人计划通过智子的多维展开来限制地球人的科学技术发展,已知智子的直径是0.00000000000016厘米,用科学记数法表示这个数( )A、米 B、 米 C、 厘米 D、厘米3. 若分式 的值为0,则x的值为( )A、4 B、- 4 C、4或-4 D、04. 在平面直角坐标系中,已知点和点关于轴对称,则的值( )A、 B、 C、 D、5. 下列多项式中,不能用完全平方公式分解因式的是( )A、 B、 C、 D、6. 下列分式计算错误的是( )A、 B、 C、 D、7. 计算的结果为( )A、3 B、 C、 D、8. 若式子有意义,则x满足的条件是( )A、且 B、且 C、且 D、且且9. 如图,在等边中,是边上的中线,点在上,连接 , 在的右侧作等边 , 连接 , 当周长最小时,则的大小是( )
2. 科幻作品《三体》一书中,三体人计划通过智子的多维展开来限制地球人的科学技术发展,已知智子的直径是0.00000000000016厘米,用科学记数法表示这个数( )A、米 B、 米 C、 厘米 D、厘米3. 若分式 的值为0,则x的值为( )A、4 B、- 4 C、4或-4 D、04. 在平面直角坐标系中,已知点和点关于轴对称,则的值( )A、 B、 C、 D、5. 下列多项式中,不能用完全平方公式分解因式的是( )A、 B、 C、 D、6. 下列分式计算错误的是( )A、 B、 C、 D、7. 计算的结果为( )A、3 B、 C、 D、8. 若式子有意义,则x满足的条件是( )A、且 B、且 C、且 D、且且9. 如图,在等边中,是边上的中线,点在上,连接 , 在的右侧作等边 , 连接 , 当周长最小时,则的大小是( ) A、 B、 C、 D、10. 如图,交于点 , 的平分线与的外角的平分线交于点 , , 则下列说法不正确的是( )
A、 B、 C、 D、10. 如图,交于点 , 的平分线与的外角的平分线交于点 , , 则下列说法不正确的是( ) A、 B、 C、 D、11. 小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x本笔记本,则根据题意可列方程( )A、=1 B、=1 C、=1 D、=112. 如图,已知线段上有一动点 , 分别以、为边在同方向作等边和等边 , 连接 , 交于点 , 连接 , 交于点 , 连接 , 有以下结论:①;②;③;④;⑤ . 其中正确的是( )
A、 B、 C、 D、11. 小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x本笔记本,则根据题意可列方程( )A、=1 B、=1 C、=1 D、=112. 如图,已知线段上有一动点 , 分别以、为边在同方向作等边和等边 , 连接 , 交于点 , 连接 , 交于点 , 连接 , 有以下结论:①;②;③;④;⑤ . 其中正确的是( ) A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题:本大题共54题,每小题3分,共12分.
-
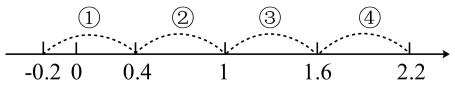
13. 已知:a、b、c是三边长,且 , 那么M0(填“>”,“<”或“=”)14. 如图,数轴上有四条线段分别标有①,②,③,④,则表示分式 的值的点应落在数轴的段.(填序号)
 15. 学习新知时,我们利用图形的拼接得到完全平方公式,小红也想探究一下图形的奥秘,她利用四块长为 , 宽为的长方形纸片,拼成如图形状.观察图片,写出代数式 , , 之间的等量关系;
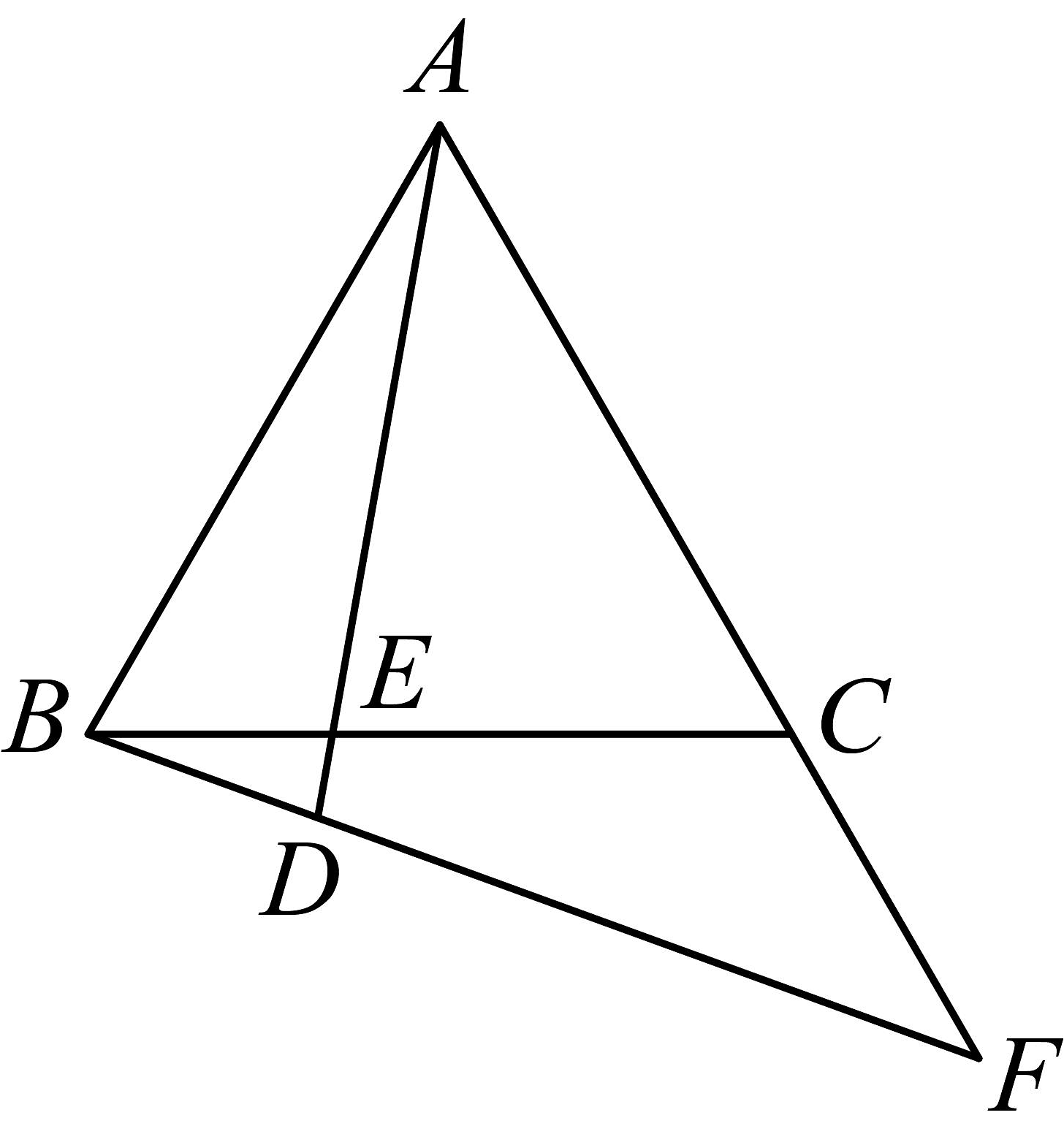
15. 学习新知时,我们利用图形的拼接得到完全平方公式,小红也想探究一下图形的奥秘,她利用四块长为 , 宽为的长方形纸片,拼成如图形状.观察图片,写出代数式 , , 之间的等量关系; 16. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .
16. 为等边三角形,点E在边上, , 在射线上取点D,使 , 连接并延长交射线于点F,则下列说法正确的是: .①当时,为等腰三角形;
②;
③在边上存在点E,使;
④ .
三、解答题:本大题共7小题,共72分.
-
17.(1)、计算:(2)、计算:(3)、分解因式:;(4)、分解因式: .18. 计算:(1)、 .(2)、先化简 , 若的取值范围是 , 且为整数,求该式的值.19. 阳光体育用品店有甲、乙两种品牌的篮球,已知乙品牌篮球的单价比甲品牌篮球的单价多元,用元购买甲品牌篮球的数量是用元购买乙品牌篮球数量的倍.(1)、求甲、乙两种品牌篮球的单价;(2)、该店在国庆节期间开展优惠活动,甲品牌篮球按原单价的折出售,乙品牌篮球按原单价的折出售,某校计划在国庆节期间在该店购买甲、乙两种品牌篮球共个,总费用不超过元,那么最多可购买多少个乙品牌篮球?20. 如图,在平面直角坐标系中,各顶点的坐标分别为 , , .
 (1)、作出与关于轴对称的图形;(2)、已知点 , 直线轴,求点的坐标.21. 如图,在等边中,点是边上一点(点不与端点重合).作点关于直线的对称点 , 连接 , 在射线上取一点 , 使 , 与所在直线交于点 .
(1)、作出与关于轴对称的图形;(2)、已知点 , 直线轴,求点的坐标.21. 如图,在等边中,点是边上一点(点不与端点重合).作点关于直线的对称点 , 连接 , 在射线上取一点 , 使 , 与所在直线交于点 . (1)、求证:;(2)、若 , 求的长;(3)、当在边上运动时,判断 , , 面积之间的数量关系,并说明理由.22. 基本知识:通过用两种不同方法计算图1的面积,发现:恒成立.基于此,请解答下列问题:
(1)、求证:;(2)、若 , 求的长;(3)、当在边上运动时,判断 , , 面积之间的数量关系,并说明理由.22. 基本知识:通过用两种不同方法计算图1的面积,发现:恒成立.基于此,请解答下列问题: (1)、直接应用:若 , , 直接写出的值为 ;(2)、类比应用:若 , 则 ;(3)、拓展迁移:为落实国家劳动实践教育的政策,使同学们体验劳动的快乐,掌握劳动技能.某学校计划组织八年级的学生在学校实践园开展劳动实践活动.首先在实践园用栅栏围成一个区域,用来种植草坪(如图2),其中于点A,与两边的长度和为 , 然后再以 , 为边分别向外扩建成正方形和正方形的用地,分别种植三角梅和月季花,向外扩建的两个正方形面积和为 . 请根据题意求种植草坪的的面积.23. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.
(1)、直接应用:若 , , 直接写出的值为 ;(2)、类比应用:若 , 则 ;(3)、拓展迁移:为落实国家劳动实践教育的政策,使同学们体验劳动的快乐,掌握劳动技能.某学校计划组织八年级的学生在学校实践园开展劳动实践活动.首先在实践园用栅栏围成一个区域,用来种植草坪(如图2),其中于点A,与两边的长度和为 , 然后再以 , 为边分别向外扩建成正方形和正方形的用地,分别种植三角梅和月季花,向外扩建的两个正方形面积和为 . 请根据题意求种植草坪的的面积.23. “一线三等角”模型是平面几何图形中的重要模型之一,“一线三等角”指的是图形中出现同一条直线上有3个相等的情况,在学习过程中,我们发现“一线三等角”模型的出现,还经常会伴随着出现全等三角形.根据对材料的理解解决以下问题∶
 (1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.
(1)、如图1, , . 猜想 , , 之间的关系:(2)、如图2,将(1)中条件改为 , , 请问(1)中的结论是否成立?若成立,请给出证明;若不成立,请说明理由;(3)、如图3,在中,点为上一点, , , , , 请直接写出的长.