相关试卷

1、先化简，再求值： $(4 a b^{3} - 8 a^{2} b^{2}) \div 4 a b + (2 a + b) (2 a - b)$ ，其中a、b满足 $\sqrt{a - 2} + | b + 1 | = 0$ ．

查看解析
2、已知 $a + 2$ 的立方根是 $3$ ， $3 a + b - 1$ 的算术平方根是 $4$ ， $c$ 是 $\sqrt{13}$ 的整数部分．

(1)、求 $a$ ， $b$ ， $c$ 的值；

(2)、求 $3 a - b + c$ 的平方根．

查看解析
3、已知 $\sqrt{a - 3} + \sqrt{3 - a} = 0$ ， $3 b - 4$ 的立方根是2，c是 $\sqrt{6}$ 的整数部分．

(1)、求a、b、c的值；

(2)、求 $a + 6 b - c$ 的平方根．

查看解析
4、已知实数 $a$ ， $b$ ， $c$ 在数轴上对应的点如图所示，化简 $\sqrt{(b + c)^{2}} + | a - c | + \sqrt{b^{2} - 2 a b + a^{2}}$

查看解析
5、已知关于x、y的方程组 ${\begin{array}{l} a x + 7 y = 15 ① \\ 4 x - b y = - 2 ② \end{array}$ ，由于甲看错了方程①中的a得到方程组的解为 ${\begin{array}{l} x = - 2 \\ y = 1 \end{array}$ ，乙看错了方程②中的b得到方程组的解为 ${\begin{array}{l} x = 4 \\ y = 1 \end{array}$ ，求 $b^{a}$ 的算术平方根．

查看解析
6、若 ${(a - 3)}^{2} + \sqrt{b - 6} = 0$ ，则以 $a$ 、 $b$ 为边的等腰三角形的周长为.

查看解析
7、已知： $2 a - 7$ 和 $a + 4$ 是正数M的平方根， $b - 7$ 的立方根为 $- 2$ ，则 $3 a + 2 b$ 的算术平方根．

查看解析
8、月球轨道呈椭圆形，近地点平均距离为 $363300 k m$ ，用科学记数法表示363300为（精确到10000）．

查看解析
9、司南是中国古人利用磁铁制作的一种指南工具，如图，司南的形状像一把汤匙，它的长度与最大宽度之比为 $\sqrt{26} - 1$ ，若 $\sqrt{26} - 1$ 介于两个连续整数n和 $n + 1$ 之间，则n的值是．

查看解析
10、已知正数x的两个不等的平方根分别是 $2 a - 14$ 和 $a + 2$ ， $b + 1$ 的立方根为 $- 3$ ；c是 $\sqrt{5}$ 的整数部分，若 $a + \sqrt{3} c = m + n$ ，其中m为整数， $0 < n < 1$ ，则 $(n + 3) (b - m) =$ ．

查看解析
11、近似数 $8.240 \times 1 0^{5}$ 是精确到（）

A、千分位 B、千位 C、百位 D、十位

查看解析
12、若m，n为实数，且 $(m + 4)^{2} + \sqrt{n - 5} = 0$ ，则 $(m + n)^{2}$ 的值为（）

A、1 B、0 C、81 D、 $- 9$

查看解析
13、如果 $(x - 1) (x + 3) = x^{2} + a x + b$ ，那么 $a + b$ 的立方根是（）

A、1 B、 $- 1$ C、 $\pm 1$ D、 $\sqrt[3]{5}$

查看解析
14、某人的体重约为 $56.4 k g$ ，这个数是个近似数，那么这个人的体重 $x (k g)$ 的取值范围是（）

A、 $56.39 < x \leq 56.44$ B、 $56.35 \leq x < 56.45$ C、 $56.41 < x < 56.50$ D、 $56.44 \leq x < 56.59$

查看解析
15、下列说法中，错误的是（）

A、5是25的算术平方根 B、 $\sqrt{81}$ 的平方根是 $\pm 3$ C、0的平方根与算术平方根都是0 D、 ${(- 4)}^{2}$ 的平方根是 $- 4$

查看解析
16、下列各式中，正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $- \sqrt{4} = 2$ C、 $\sqrt[3]{- 27} = - 3$ D、 $\sqrt{{(- 3)}^{2}} = - 3$

查看解析
17、已知 $O$ 为直线 $M N$ 上一点，以 $O$ 为端点作射线 $O C$ ，使 $∠ C O N = 50 °$ ，将一个直角三角尺 $A O B$ 的直角顶点放在点 $O$ 处．

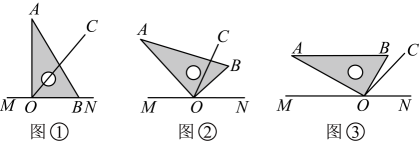(1)、如图①，若直角三角尺 $A O B$ 的一边 $O B$ 与射线 $O N$ 重合，则 $∠ A O C =$ ；

(2)、将直角三角尺 $A O B$ 摆放至如图②所示的位置时， $O A$ 恰好平分 $∠ C O M$ ，请判断 $O B$ 是否平分 $∠ C O N$ ，并说明理由；

(3)、将直角三角尺 $A O B$ 摆放至如图③所示的位置时，若恰好 $∠ A O M = 3 ∠ B O C$ ，求 $∠ B O M$ 的度数．

查看解析
18、

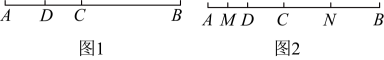(1)、如图1，点C为线段 $A B$ 上一点， $A C$ 与 $C B$ 长度之比为3：5，D为线段 $A C$ 中点．
①若 $A B = 16$ ，求 $B D$ 的长．
②点E为线段 $B D$ 的中点，若 $C E = m$ ，求 $A B$ 的长（用含m的代数式表示）．

(2)、如图2，点M为线段 $A D$ 中点，点N为线段 $B C$ 中点，若 $A B = a$ ， $C D = b$ ，请用含a ， b的代数式直接表示出 $M N$ 的长．

查看解析
19、在平整的地面上，有若干个完全相同的棱长为 $2 c m$ 的小正方体堆成一个几何体，如图所示：

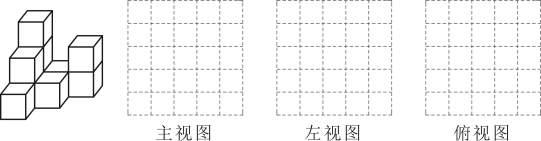(1)、这个几何体是由个小正方体组成，该几何体的体积是，请用阴影画出这个几何体从三个方向看的图形；

(2)、如果在这个几何体露在外面的表面喷上红色的漆，每平方厘米用2克，则共需克漆；

(3)、如果在这个几何体上再添加一些小正方体，并保持俯视图和左视图不变，最多可以再添加个小正方体．

查看解析
20、根据所给立体图形的三视图，

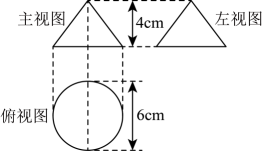(1)、写出这个立体图形的名称：；

(2)、求出这个立体图形的体积．

查看解析

上一页 576 577 578 579 580 下一页跳转