湘教版数学八年级上册 5.1 直角三角形的性质定理 第二课时 同步分层练习
试卷更新日期:2025-11-19 类型:同步测试
一、夯实基础
-
1. 在中, , , , 则等于( )A、2 B、8 C、4 D、62. 如图是某公园的一滑梯侧面图,已知 , 滑梯架的高为 , 则滑梯长为( )
 A、 B、 C、 D、3. 如图,在中, , , 是边上一点,且 , 则边的长为( )
A、 B、 C、 D、3. 如图,在中, , , 是边上一点,且 , 则边的长为( ) A、1 B、2 C、3 D、44. 如图,某商场一楼与二楼之间的电梯示意图.的长是10,则乘电梯从点B到点C上升的高度h是( )
A、1 B、2 C、3 D、44. 如图,某商场一楼与二楼之间的电梯示意图.的长是10,则乘电梯从点B到点C上升的高度h是( ) A、 B、 C、10 D、55. 在中,若 , , , 则度.6. 三角形三内角的度数之比为1:2:3,最大边的长是8cm,则最小边的长是cm.7. 如图,在中, , 以点A为圆心,为半径作弧,交边于点D,若 , 则 .
A、 B、 C、10 D、55. 在中,若 , , , 则度.6. 三角形三内角的度数之比为1:2:3,最大边的长是8cm,则最小边的长是cm.7. 如图,在中, , 以点A为圆心,为半径作弧,交边于点D,若 , 则 . 8. 如图,中, , , 过点 , 点分别作 , 的垂线相交于点 , 则 .
8. 如图,中, , , 过点 , 点分别作 , 的垂线相交于点 , 则 . 9. 在 中,∠C=90°,∠B=2∠A,∠B 和∠A各是多少度? 边AB 与BC之间有什么关系?10. 如图, , , , 平分 , 若 , 求的长.
9. 在 中,∠C=90°,∠B=2∠A,∠B 和∠A各是多少度? 边AB 与BC之间有什么关系?10. 如图, , , , 平分 , 若 , 求的长.
二、能力提升
-
11. 将一个有45°角的三角板的直角顶点放在一张宽为的纸带边沿上,另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边沿所在的直线成30°角,如图所示,则三角板的直角边的长为( )
 A、 B、 C、 D、12. 如图,已知在△ABC中,AB=AC , ∠A=120°,DE垂直平分AC , 若CD=2,则BD的长为( )
A、 B、 C、 D、12. 如图,已知在△ABC中,AB=AC , ∠A=120°,DE垂直平分AC , 若CD=2,则BD的长为( )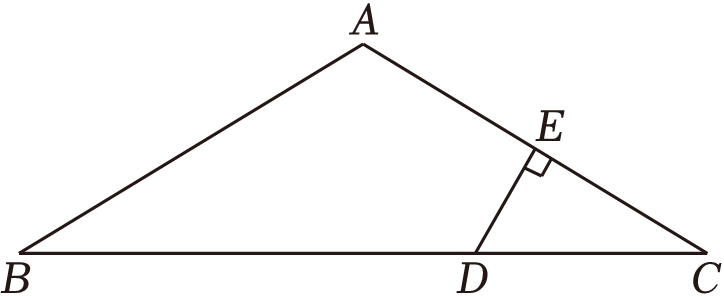 A、3 B、4 C、5 D、613. 如图,在等边中,平分交于点D,过点D作于点E,且 , 则的长为( )
A、3 B、4 C、5 D、613. 如图,在等边中,平分交于点D,过点D作于点E,且 , 则的长为( ) A、3 B、4.5 C、6 D、7.514. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.AD的长是( )
A、3 B、4.5 C、6 D、7.514. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.AD的长是( ) A、5 B、6 C、7 D、815. 如图, , , B点在的垂直平分线上,若 , 则为( )
A、5 B、6 C、7 D、815. 如图, , , B点在的垂直平分线上,若 , 则为( ) A、4 B、6 C、8 D、1016. 如图,M,A,N是直线l上的三点, , , P是直线l外一点,且 , , 若动点Q从点M出发,向点N移动,移动到点N停止,在APQ形状的变化过程中,依次出现的特殊三角形是( )
A、4 B、6 C、8 D、1016. 如图,M,A,N是直线l上的三点, , , P是直线l外一点,且 , , 若动点Q从点M出发,向点N移动,移动到点N停止,在APQ形状的变化过程中,依次出现的特殊三角形是( ) A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形17. 如图,已知 , 点在边上, , 点M,N在边上, , 若 , 求的长
A、直角三角形—等边三角形—直角三角形—等腰三角形 B、直角三角形—等腰三角形—直角三角形—等边三角形 C、等腰三角形—直角三角形—等腰三角形—直角三角形 D、等腰三角形—直角三角形—等边三角形—直角三角形17. 如图,已知 , 点在边上, , 点M,N在边上, , 若 , 求的长 18. 如图,将一副三角尺如图所示叠放在一起,若AB=12cm,则阴影部分的面积是cm2 .
18. 如图,将一副三角尺如图所示叠放在一起,若AB=12cm,则阴影部分的面积是cm2 . 19. 如图①所示的是校门口的双翼闸门,当它的双翼展开时,如图②所示,双翼边缘的端点与之间的距离为厘米,双翼的边缘厘米,且与闸机箱侧立面的夹角 , 则当双翼收起时,可以通过闸机的最大宽度为厘米.
19. 如图①所示的是校门口的双翼闸门,当它的双翼展开时,如图②所示,双翼边缘的端点与之间的距离为厘米,双翼的边缘厘米,且与闸机箱侧立面的夹角 , 则当双翼收起时,可以通过闸机的最大宽度为厘米. 20. 如图所示,在中. , , 线段的垂直平分线分别交、于点、 , 连接 . 若 , 则的长为 .
20. 如图所示,在中. , , 线段的垂直平分线分别交、于点、 , 连接 . 若 , 则的长为 . 21. 如图,中, , D为上一动点,垂直平分分别交于E,交于F,则 .
21. 如图,中, , D为上一动点,垂直平分分别交于E,交于F,则 . 22. 如图,在中, , 为的中点, , 点在上,且 , 则的大小为 .
22. 如图,在中, , 为的中点, , 点在上,且 , 则的大小为 . 23. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
23. 如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长. 24. 如图,在中, , 平分 , 于 , 连接 , 交于点 .
24. 如图,在中, , 平分 , 于 , 连接 , 交于点 . (1)、求证:是线段的垂直平分线;(2)、若 , , 求的长.
(1)、求证:是线段的垂直平分线;(2)、若 , , 求的长.三、拓展创新
-
25. 某轮船由西向东航行,在A处测得小岛的方位是北偏东 , 又继续航行16海里后,在处测得小岛的方位是北偏东 , 求:
 (1)、此时轮船与小岛的距离是多少海里?(2)、小岛方圆7.5海里内有暗礁,如果轮船继续向东行驶,请问轮船有没有触礁的危险?请说明理由.26. 如图 , 点分别是边长为的等边边上的动点,点从顶点 , 点从顶点同时出发,且它们的速度都为 .
(1)、此时轮船与小岛的距离是多少海里?(2)、小岛方圆7.5海里内有暗礁,如果轮船继续向东行驶,请问轮船有没有触礁的危险?请说明理由.26. 如图 , 点分别是边长为的等边边上的动点,点从顶点 , 点从顶点同时出发,且它们的速度都为 . (1)、连接交于点 , 则在运动的过程中,变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)、试求何时是直角三角形?(3)、如图 , 若点在运动到终点后继续在射线上运动,直线交点为 , 则变化吗?若变化,则说明理由,若不变,则求出它的度数.
(1)、连接交于点 , 则在运动的过程中,变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)、试求何时是直角三角形?(3)、如图 , 若点在运动到终点后继续在射线上运动,直线交点为 , 则变化吗?若变化,则说明理由,若不变,则求出它的度数.