湘教版数学 八年级上册 5.1 直角三角形的性质定理 第一课时 同步分层练习
试卷更新日期:2025-11-19 类型:同步测试
一、夯实基础
-
1. 在中, , 则此三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形2. 已知在 Rt△ABC 中,斜边上的中线 CD=5cm,则斜边 AB的长为( )A、5 B、6 C、8 D、103. 在中, , 则的度数为( )A、 B、 C、 D、4. 如图,在中, , 是边的中点,若 , 则的长是( )
 A、 B、 C、 D、5. 一个三角形三个内角的度数之比是 , 则这个三角形一定是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形6. 如图1,这是一种太阳能热水器,它是一种环保、经济的家庭热水供应设备,备受大众喜爱。该太阳能热水器安装后,我们可以将其看作△ABC(如图2)。为了使其更加牢固,安装工人增加了AE,DE两根支架。若支架AE与地面CE呈 60°,支架DE⊥AB,∠C=90°,∠BAC=2∠B,AC=1.2m,则BD的长为( )
A、 B、 C、 D、5. 一个三角形三个内角的度数之比是 , 则这个三角形一定是( )A、直角三角形 B、等腰三角形 C、钝角三角形 D、锐角三角形6. 如图1,这是一种太阳能热水器,它是一种环保、经济的家庭热水供应设备,备受大众喜爱。该太阳能热水器安装后,我们可以将其看作△ABC(如图2)。为了使其更加牢固,安装工人增加了AE,DE两根支架。若支架AE与地面CE呈 60°,支架DE⊥AB,∠C=90°,∠BAC=2∠B,AC=1.2m,则BD的长为( ) A、1m B、1.2m C、1.4m D、1.5m7. 如图, , 过点作于点 . 若 , 则的度数为( )
A、1m B、1.2m C、1.4m D、1.5m7. 如图, , 过点作于点 . 若 , 则的度数为( ) A、 B、 C、 D、8. 直角三角形两锐角之差是12°,则较大的一个锐角是°.9. 如图,在中, , 是的中点,若 , 则的长为 .
A、 B、 C、 D、8. 直角三角形两锐角之差是12°,则较大的一个锐角是°.9. 如图,在中, , 是的中点,若 , 则的长为 . 10. 下列四个条件:
10. 下列四个条件:①在△ABC 中, ∠A, ∠B 都是锐角;
②△ABC的三个内角的度数之比是1:2:3;
③在△ABC中, ∠A-∠B=∠C;
④△ABC的三个外角的度数之比是3:4:5.
其中能确定△ABC 是直角三角形的是(只填序号).
11. 如图,锐角的高 , 相交于 , 若 , , , 则的长为 . 12. 如图,在中,是边上的高,平分 , 若 , , 求和的度数.
12. 如图,在中,是边上的高,平分 , 若 , , 求和的度数.
二、能力提升
-
13. 具备下列条件的中,不是直角三角形的是( )A、 B、 C、 D、14. 如图,在等边中, , , , 交于点 , 则的度数是( )
 A、 B、 C、 D、15. 如图,在中,是角平分线, , 垂足为D,则与的关系是( )
A、 B、 C、 D、15. 如图,在中,是角平分线, , 垂足为D,则与的关系是( ) A、 B、 C、 D、16. 如图,在中,于点于点D,点F是的中点,连接设 , 则( )
A、 B、 C、 D、16. 如图,在中,于点于点D,点F是的中点,连接设 , 则( )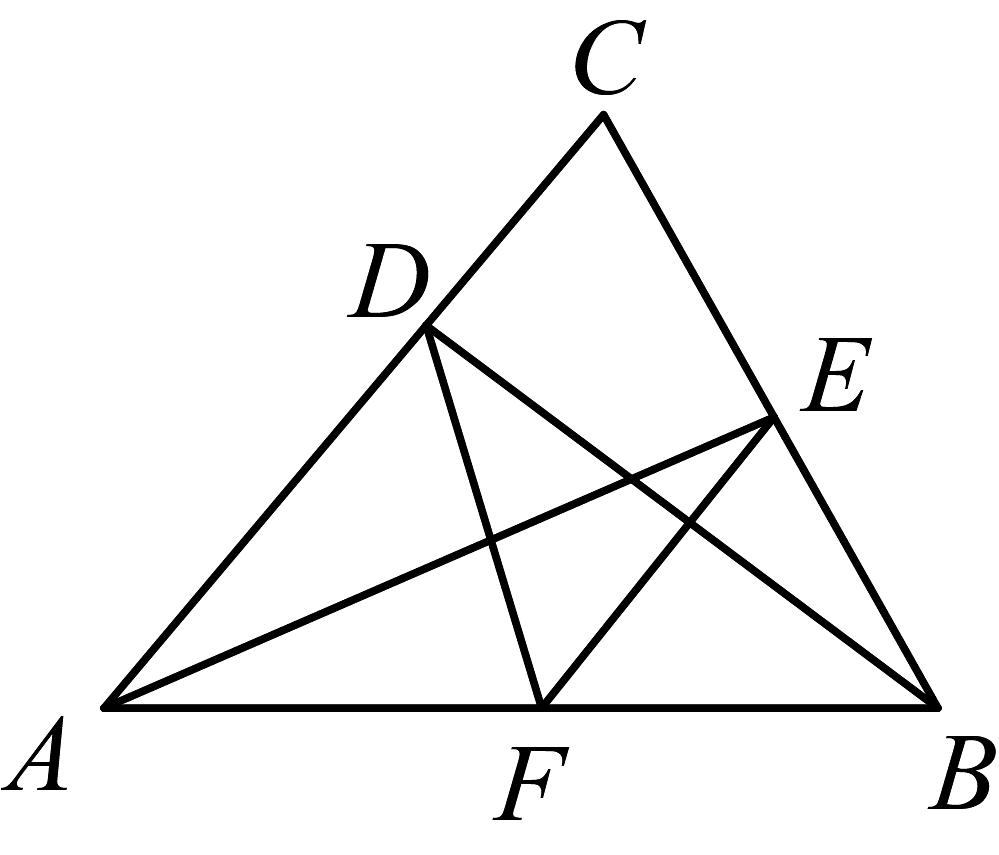 A、 B、 C、 D、17. 如图,一副三角板叠放在一起, , , , 则的度数为( )
A、 B、 C、 D、17. 如图,一副三角板叠放在一起, , , , 则的度数为( ) A、 B、 C、 D、18. 如图,在的正方形网格中,则 .
A、 B、 C、 D、18. 如图,在的正方形网格中,则 . 19. 如图,中, , 点E为的中点,点D在上,且、相交于点F,若 , 则等于 .
19. 如图,中, , 点E为的中点,点D在上,且、相交于点F,若 , 则等于 . 20. 如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=度.
20. 如图,在直角三角形ABC中,两锐角平分线AM、BN所夹的钝角∠AOB=度. 21. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .
21. 如图,在中,是边上的高线,是边上的中线,于点G,且 . 若 , 则的度数是 .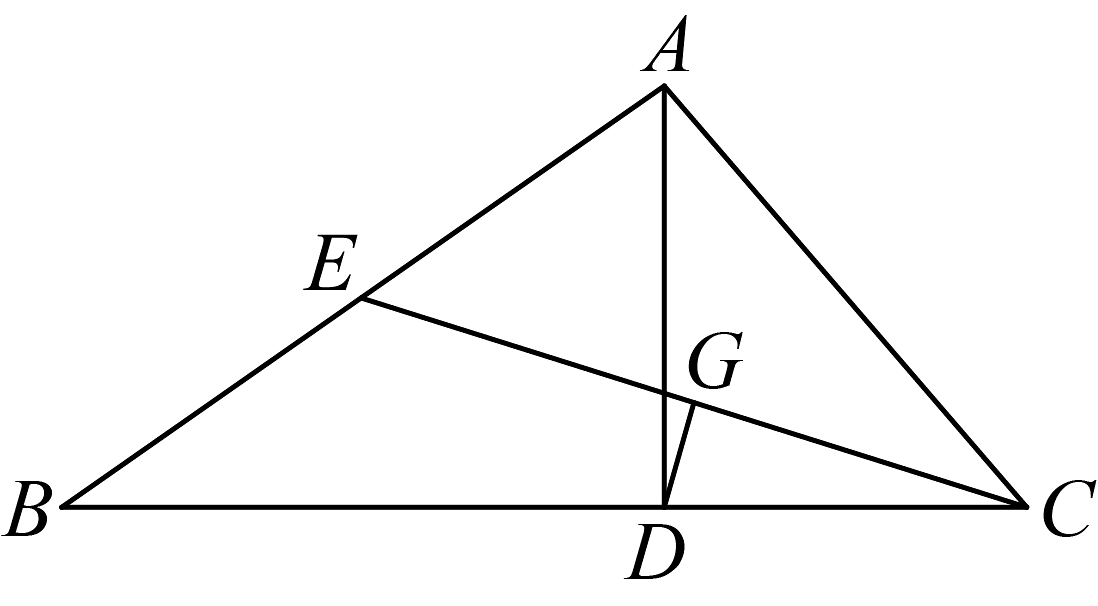 22. 如图所示,是的角平分线,是的高,且 .
22. 如图所示,是的角平分线,是的高,且 . (1)、求的度数;(2)、求的度数.23. 如图,和分别位于异侧, , 点O是的中点,连接 , , .
(1)、求的度数;(2)、求的度数.23. 如图,和分别位于异侧, , 点O是的中点,连接 , , . (1)、若 , , 求的度数:(2)、若锐角 , 求的度数(用的代数式表示).
(1)、若 , , 求的度数:(2)、若锐角 , 求的度数(用的代数式表示).三、拓展创新

