湘教版数学 八年级上册4.5等腰三角形 第二课时 同步分层练习
试卷更新日期:2025-11-18 类型:同步测试
一、夯实基础
-
1. 下列条件中,可以判定是等腰三角形的是( )A、 B、 C、 D、2. 在△ABC中,已知∠A=∠B=2∠C,则△ABC是( )A、等腰三角形 B、等边三角形 C、直角三角形 D、等腰直角三角形3. 已知三角形的两个内角,能判定这个三角形是等腰三角形的是( ).A、30°,60° B、40°,70° C、50°,60° D、100°,30°4. 如图,∠A=36°,∠ADB=108°,则图中共有等腰三角形( )
 A、1个 B、2个 C、3个 D、4个5. 如图,中,点在边上,若 , 则下列结论正确的是( )
A、1个 B、2个 C、3个 D、4个5. 如图,中,点在边上,若 , 则下列结论正确的是( ) A、 B、 C、 D、6. 如图, , D点在边上,若 , 则的度数为( )
A、 B、 C、 D、6. 如图, , D点在边上,若 , 则的度数为( ) A、 B、 C、 D、7. 如图,点D在AB上,AB=AC,AD=DC=BC,则图中的等腰三角形共有( )
A、 B、 C、 D、7. 如图,点D在AB上,AB=AC,AD=DC=BC,则图中的等腰三角形共有( ) A、1个 B、2个 C、3个 D、无法确定8. 如图,在中,以点B为圆心,适当长度为半径画弧,分别交、于点P、Q,再分别以点P、Q为圆心,大于长度为半径画弧,两弧交于点M,连接交于点E,过点E做交于点D.若 , , 则的周长为 .
A、1个 B、2个 C、3个 D、无法确定8. 如图,在中,以点B为圆心,适当长度为半径画弧,分别交、于点P、Q,再分别以点P、Q为圆心,大于长度为半径画弧,两弧交于点M,连接交于点E,过点E做交于点D.若 , , 则的周长为 . 9. 如图,已知交于点 , 且 , 若 , , 则的长为 .
9. 如图,已知交于点 , 且 , 若 , , 则的长为 . 10. 在△ABC中,∠A=40°,∠B=70° ,则∠C= 度,△ABC是三角形.11. 如图,在与中, , , 与交于点E.求证: .
10. 在△ABC中,∠A=40°,∠B=70° ,则∠C= 度,△ABC是三角形.11. 如图,在与中, , , 与交于点E.求证: .
二、能力提升
-
12. 已知、、是的三边,且满足 , 则的形状是( )A、等边三角形 B、等腰三角形 C、直角三角形 D、不能确定13. 如图,在方格纸上,A,B是格点,网格中存在格点C使得是以为顶角的等腰三角形,这样的格点C的个数为( )
 A、4 B、5 C、6 D、714. 如图,上午10时,一条船从海岛出发,以(海里/时,)的速度向正北航行,12时到达海岛处.从 , 望灯塔 , 测得 , . 求从海岛到灯塔的距离为( )
A、4 B、5 C、6 D、714. 如图,上午10时,一条船从海岛出发,以(海里/时,)的速度向正北航行,12时到达海岛处.从 , 望灯塔 , 测得 , . 求从海岛到灯塔的距离为( ) A、12海里 B、24海里 C、20海里 D、36海里15. 如图,在中, , , 为边上的动点,连接 , 作 , 交于点 , 交于点 , 连接 . 对于下列两个命题的判断: ①当平分时,;②当为边上中线时, . 正确的是( )
A、12海里 B、24海里 C、20海里 D、36海里15. 如图,在中, , , 为边上的动点,连接 , 作 , 交于点 , 交于点 , 连接 . 对于下列两个命题的判断: ①当平分时,;②当为边上中线时, . 正确的是( ) A、都是真命题 B、都是假命题 C、①是真命题②是假命题 D、①是假命题②是真命题16. 如图,在中, , 的平分线交于点 , 过点作交于点 , 交于点 . 若 , , , 则的周长是( )
A、都是真命题 B、都是假命题 C、①是真命题②是假命题 D、①是假命题②是真命题16. 如图,在中, , 的平分线交于点 , 过点作交于点 , 交于点 . 若 , , , 则的周长是( ) A、17 B、18 C、20 D、2217. 如图,在中, , D,E分别是线段上的一点,根据下列条件之一,不能确定是等腰三角形的是( )
A、17 B、18 C、20 D、2217. 如图,在中, , D,E分别是线段上的一点,根据下列条件之一,不能确定是等腰三角形的是( ) A、 B、 C、 D、18. 如图,为内一点,平分 , , , 若 , , 则的长为 .
A、 B、 C、 D、18. 如图,为内一点,平分 , , , 若 , , 则的长为 .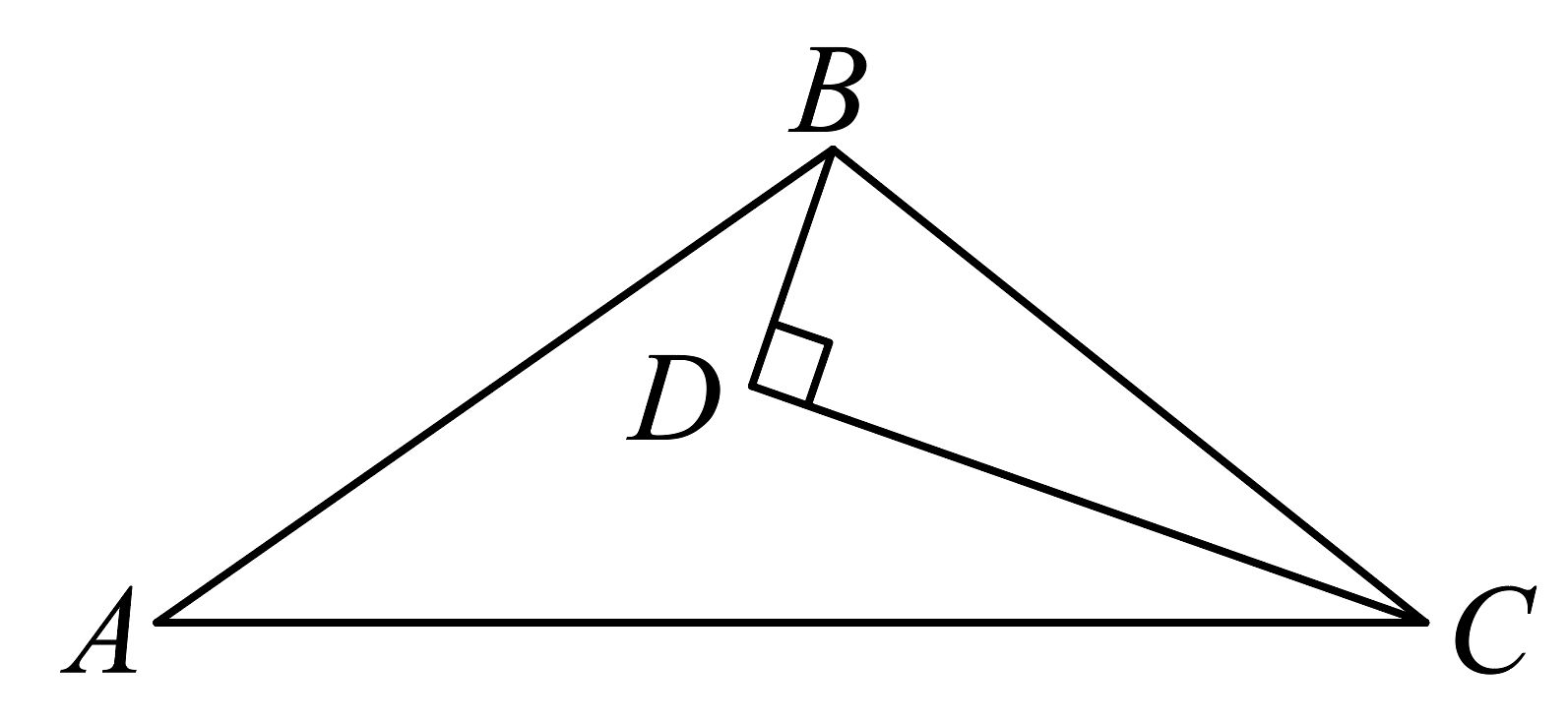 19. 如图,在中,为边上的中线,为上一点,连接并延长交于点 , 若 , , , 则的长为 .
19. 如图,在中,为边上的中线,为上一点,连接并延长交于点 , 若 , , , 则的长为 . 20. 如图,B是射线上动点, , 若为等腰三角形,则的度数可能是 .
20. 如图,B是射线上动点, , 若为等腰三角形,则的度数可能是 . 21. 如图, AD∥BC, BD平分∠ABC.求证AB=AD.
21. 如图, AD∥BC, BD平分∠ABC.求证AB=AD. 22. 如图,在中, , 是边上的中点,连接 , 平分交于点 , 过点作交于点 .
22. 如图,在中, , 是边上的中点,连接 , 平分交于点 , 过点作交于点 . (1)、若 , 求的度数;(2)、求证: .
(1)、若 , 求的度数;(2)、求证: .三、拓展创新
-
23. 如图①, , , , 相交于点M,连接 .
 (1)、求证:;(2)、用含的式子表示的度数;(3)、当时,的中点分别为点P,Q,连接 , 如图②,判断的形状,并证明.24. 课外兴趣小组活动时,老师提出了如下问题:
(1)、求证:;(2)、用含的式子表示的度数;(3)、当时,的中点分别为点P,Q,连接 , 如图②,判断的形状,并证明.24. 课外兴趣小组活动时,老师提出了如下问题:
如图1, 中,若 , 求边上的中线的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长到E,使 , 请根据小明的方法思考:
(1)由已知和作图能得到的理由是 .
A. B. C. D.
(2)求得的取值范围是 .
A. B. C. D.
【感悟】
解题时,条件中若出现“中点”“中线”字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,是 的中线,交于E,交于F,且 , 求证: .