人教版八（上）数学第十七单元质量检测培优卷

试卷更新日期：2025-11-17 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 若长和宽分别是 $a ， b$ 的长方形的周长为10，面积为4，则 $a^{2} b + a b^{2}$ 的值为（）

A、14 B、16 C、20 D、40

查看试题解析
2. 若实数x，y，z满足 ${(x - z)}^{2} - 4 (x - y) (y - z) = 0$ ，则下列式子一定成立的是（）

A、x+y+z=0 B、x+y-2z=0 C、y+z-2x=0 D、z+x-2y=0

查看试题解析
3. 已知 $x^{2} + a x - 12$ 能分解成两个整系数的一次因式的乘积，则符合条件的整数a 的个数是( ).

A、3个 B、4个 C、6 个 D、8个

查看试题解析
4. 已知 $△ A B C$ 的三边 $a$ ， $b$ ， $c$ 满足 $a |a + c| - b c - a b = 0$ ，则 $△ A B C$ 的形状为（）

A、等边三角形 B、直角三角形 C、等腰三角形 D、等腰直角三角形

查看试题解析
5. 图2是图1中长方体的三视图，用S表示面积， $S_{主} = x^{2} + 3 x, S_{左} = x^{2} + x,$ 则 $S_{俯} =$ （　　）

A、 $x^{2} + 3 x + 2$ B、 $x^{2} + 2 x + 1$ C、 $x^{2} + 4 x + 3$ D、 $2 x^{2} + 4 x$

查看试题解析
6. 已知实数 $a$ 满足 $a^{2} - 2 a - 1 = 0$ ，则代数式 $2 a^{3} - a^{2} - 8 a + 4$ 的值为（）

A、9 B、7 C、0 D、 $- 9$

查看试题解析
7. 当n为自然数时，（n+1）²﹣（n﹣3）²一定能（）

A、被5整除 B、被6整除 C、被7整除 D、被8整除

查看试题解析
8. 因式分解x²+mx-12=(x+p)(x+q)，其中m，p，q都为整数，则这样的m的最大值为（）

A、1 B、4 C、11 D、12

查看试题解析
9. 已知 $x$ ， $y$ ， $z$ 都是正整数，其中 $x > y$ ，且 $x^{2} - x z - x y + y z = 23$ ，设 $a = x - z$ ，则 $[(3 a - 1) (a + 2) - 5 a + 2] \div a =$ （）

A、3 B、69 C、3或69 D、2或46

查看试题解析
10. 在日常生活中如取款、上网等都需要密码，有一种用“因式分解”法产生的密码记忆方便．原理是：如对于多项式x⁴-y⁴ ，因式分解的结果是（x-y）（x+y）（x²+y²），若取x=9，y=9，则各个因式的值是：x-y=0，x+y=18，x²+y²=162，于是就可以把“018162”作为一个六位数的密码．对于多项式x³-xy² ，取x=30，y=20，用上述方法产生的密码不可能是（）

A、301050 B、305010 C、103020 D、501030

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分

11. 若多项式 $(x + 2) (2 x - 1) - (x + 2)$ 可以因式分解成 $2 (x + m) (x + n)$ ，则 $m - n$ 的值是．

查看试题解析
12. 若 $a - b = - 7$ ，则 $a^{2} - b^{2} + 14 b$ 的值是．

查看试题解析
13. 下列各式：① $- x^{2} - y^{2}$ ；② $- \frac{1}{4} a^{2} b^{2} + 1$ ；③ $a^{2} + a b + b^{2}$ ；④ $\frac{1}{4} - m n + m^{2} n^{2}$ ，能用公式法分解因式的是（填序号）．

查看试题解析
14. 分解因式 $x^{2} + 3 x y + 2 y^{2} + 4 x + 5 y + 3 =$ ．

查看试题解析
15. 整数x，y满足方程2xy+x+y=83，则x+y=.

查看试题解析

三、解答题：本大题共8小题，共75分

16. 已知a、b、c是△ABC的三边长，且a²+2b²+c²﹣2b（a+c）=0，试判断△ABC的形状，并证明你的结论．

查看试题解析
17. 阅读材料： $a^{3} - b^{3} + a^{2} b - a b^{2} = (a^{3} + a^{2} b) - (b^{3} + a b^{2})$
$= a^{2} (a + b) - b^{2} (a + b)$
＝（ ▲ ） $= (a + b)$
＝ ▲ ．

(1)、请把阅读材料补充完整；

(2)、分解因式： $4 x^{2} - 2 x - y^{2} - y$ ；

(3)、已知 $a$ ， $b$ ， $c$ 为 $△ A B C$ 的三边长，若 $a^{2} + b^{2} + 2 c^{2} - 2 a c - 2 b c = 0$ ，试判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
18. 请认真观察图形，解答下列问题：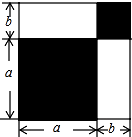

(1)、根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；

(2)、由（1），你能得到怎样的等量关系？请用等式表示；

(3)、如果图中的a，b（a＞b）满足a²＋b²＝53，ab＝14，求：①a＋b的值；②a⁴－b⁴的值．

查看试题解析

19. 阅读下面材料，在代数式中，我们把一个二次多项式化为一个完全平方式与一个常数的和的方法叫做配方法。配方法是一种重要的解决问题的数学方法，它不仅可以将一个看似不能分解的多项式因式分解，还能求代数式最大值，最小值等问题．

例如：求代数式： $x^{2} - 12 x + 2020$ 的最小值

解：原式 $= x^{2} - 12 x + 6^{2} - 6^{2} + 2020$

$= {(x - 6)}^{2} + 1984$

∵ ${(x - 6)}^{2} \geq 0$

∴当x=6时， ${(x - 6)}^{2}$ 的值最小，最小值为0

∴ ${(x - 6)}^{2} + 1984 \geq 1984$

∴当 ${(x - 6)}^{2} = 0$ 时， ${(x - 6)}^{2} + 1984$ 的值最小，最小值为1984

∴代数式： $x^{2} - 12 x + 2020$ 的最小值是1984

例如：分解因式： $x^{2} - 120 x + 3456$

解：原式 $= x^{2} - 2 \times 60 x + 60^{2} - 60^{2} + 3456$

$= {(x - 60)}^{2} - 144$

$= {(x - 60)}^{2} - 12^{2}$

$= (x - 60 + 12) (x - 60 - 12)$

$= (x - 48) (x - 72)$

（1）分解因式 $x^{2} - 46 x + 520$ ；

（2）若 $y = - x^{2} + 2 x + 1313$ ，求y的最大值；

（2）当m，n为何值时，代数式 $m^{2} - 2 m n - 2 m + 2 n^{2} - 4 n + 2030$ 有最小值，并求出这个最小值．

查看试题解析

20. 综合与实践
下面是某同学对多项式 $(x^{2} - 4 x) (x^{2} - 4 x + 8) + 16$ 进行因式分解的过程：

解：设 $x^{2} - 4 x = y$ ，

原式 $= y (y + 8) + 16$ （第一步）

$= y^{2} + 8 y + 16$ （第二步）

$= {(y + 4)}^{2}$ （第三步）

$= {(x^{2} - 4 x + 4)}^{2}$ （第四步）．

回答下列问题：

(1)、该同学第二步到第三步运用了________．

A、提取公因式 B、平方差公式 C、两数差的完全平方公式 D、两数和的完全平方公式

(2)、该同学因式分解的结果是否彻底？（填“彻底”或“不彻底”），若不彻底，则该因式分解的最终结果为．

(3)、请你模仿上述方法，对多项式 $(x^{2} - 2 x - 1) (x^{2} - 2 x + 3) + 4$ 进行因式分解．

查看试题解析
21. 先阅读下列材料：我们已经学过将一个多项式分解因式的方法有提公因式法和运用公式法，其实分解因式的方法还有分组分解法、拆项法、十字相乘法等等．
$(1)$ 分组分解法：将一个多项式适当分组后，可提公因式或运用公式继续分解的方法 $.$ 如：
$① a x + b y + b x + a y$
$= (a x + b x) + (a y + b y)$
$= x (a + b) + y (a + b)$
$= (a + b) (x + y)$
$② 2 x y + y^{2} - 1 + x^{2}$
$= x^{2} + 2 x y + y^{2} - 1$
$= (x + y)^{2} - 1$
$= (x + y + 1) (x + y - 1)$
$(2)$ 拆项法：将一个多项式的某一项拆成两项后，可提公因式或运用公式继续分解的方法 $.$ 如：
$x^{2} + 2 x - 3$
$= x^{2} + 2 x + 1 - 4$
$= (x + 1)^{2} - 2^{2}$
$= (x + 1 + 2) (x + 1 - 2)$
$= (x + 3) (x - 1)$
请你仿照以上方法，探索并解决下列问题：

(1)、分解因式： $a^{2} - b^{2} + a - b$ ；

(2)、分解因式： $a^{2} + 4 a b - 5 b^{2}$ ；

(3)、多项式 $x^{2} - 6 x + 1$ 有最小值吗？如果有，当它取最小值时 $x$ 的值为多少？

查看试题解析
22. 小磊和小轩在课外练习中碰到了一个问题，需要对多项式 $x^{3} -2 x^{2} -7 x +2$ 进行因式分解．小磊认为该整式一定有一个因式 $x +2$ ，小轩认为必有因式是 $x -2$ ，两人找到老师寻求帮助．老师提供了一个方法：因式分解是整式乘法的逆运算．若整式A能被整式B整除，则B必为A的一个因式．老师给出了演算方法：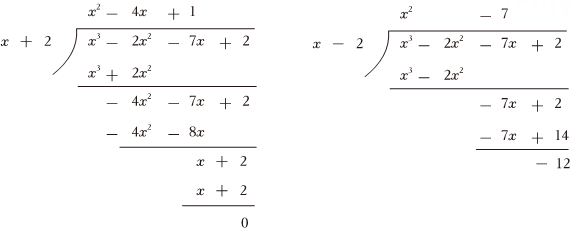

(1)、观察老师的演算后，你认为同学的想法是对的；

(2)、已知多项式 $x^{3} -6 x^{2} +7 x +6$ 的其中一个因式为 $x -3$ ，请试着根据老师的方法列出演算过程，并将多项式 $x^{3} -6 x^{2} +7 x +6$ 进行因式分解；

(3)、若多项式 $x^{3} -3 x^{2} + mx + n$ 能因式分解成 $x +1$ 与另一个完全平方式，求 $m$ 与 $n$ 的值．

查看试题解析
23. 阅读材料
小明遇到这样一个问题：求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．

小明想通过计算（x+2）（2x+3）（3x+4）所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法．

他决定从简单情况开始，先找（x+2）（2x+3）所得多项式中的一次项系数．通过观察发现：

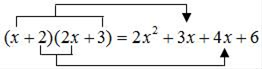
也就是说，只需用x+2中的一次项系数1乘以2x+3中的常数项3，再用x+2中的常数项2乘以2x+3中的一次项系数2，两个积相加1×3+2×2=7，即可得到一次项系数．

延续上面的方法，求计算（x+2）（2x+3）（3x+4）所得多项式的一次项系数．可以先用x+2的一次项系数1，2x+3的常数项3，3x+4的常数项4，相乘得到12；再用2x+3的一次项系数2，x+2的常数项2，3x+4的常数项4，相乘得到16；然后用3x+4的一次项系数3，x+2的常数项2，2x+3的常数项3，相乘得到18．最后将12，16，18相加，得到的一次项系数为46．

参考小明思考问题的方法，解决下列问题：

(1)、计算（2x+1）（3x+2）所得多项式的一次项系数为．

(2)、计算（x+1）（3x+2）（4x﹣3）所得多项式的一次项系数为．

(3)、若计算（x²+x+1）（x²﹣3x+a）（2x﹣1）所得多项式的一次项系数为0，则a= ．

(4)、若x²﹣3x+1是x⁴+ax²+bx+2的一个因式，则2a+b的值为．

查看试题解析