-
1、规定两数a,b之间的一种运算,记作::如果 , 那么
例如:因为 , 所以 .
(1)、根据上述规定,填空:______;(2)、若 , , 且 , 求的值;(3)、①若 , 请你尝试证明:;②进一步探究这种运算时发现一个结论: , 结合①,②探索的结论,计算:_____.
-
2、比较大小:(填“”、“”或“”).
-
3、某学校在本学期开展数学拓展活动,为了解开展数学拓展活动后学生不同阶段的学习效果,决定随机抽取七年级部分学生进行两次跟踪测评(两次随机抽取的学生人数相同),第一次是开展数学拓展活动初期的学习质量测评,第二次是开展数学拓展活动个月后的学习质量测评.根据测评的数学成绩制作了第一次测评的数学成绩频数分布直方图(如图,每一组包括左边端点,不包括右边端点)和第二次测评的数学成绩频数分布表(如表).
第二次测评的数学成绩频数分布表:
成绩
频数
根据以上图表信息,完成下列问题:
第一次测评的数学成绩频数分布直方图

(1)______;
(2)若分及以上为优秀.
①开展数学拓展活动个月后,请估计该校名七年级学生数学成绩优秀的人数;
②请分别计算两次测评数学成绩的优秀率,并对开展数学拓展活动的效果进行分析.
-
4、小明在计算时,不小心把一个运算符号写错了(“”错写成“”或“”错写成“”),结果算成了 , 则原式从左往右数,第个运算符号写错了.
-
5、如图1,内接于 , , , 点E为上一点,点F为的中点,连结并延长与交于点G,连 , .
 (1)、求证: .(2)、如图2,当经过圆心O时,
(1)、求证: .(2)、如图2,当经过圆心O时,①求的长;
②记 , 的面积分别为 . 则 .
-
6、如图是由小正方形组成的网格.每个小正方形的顶点叫做格点,请用一把无刻度直尺及圆规借助网格根据要求作图,要求保留作图痕迹.
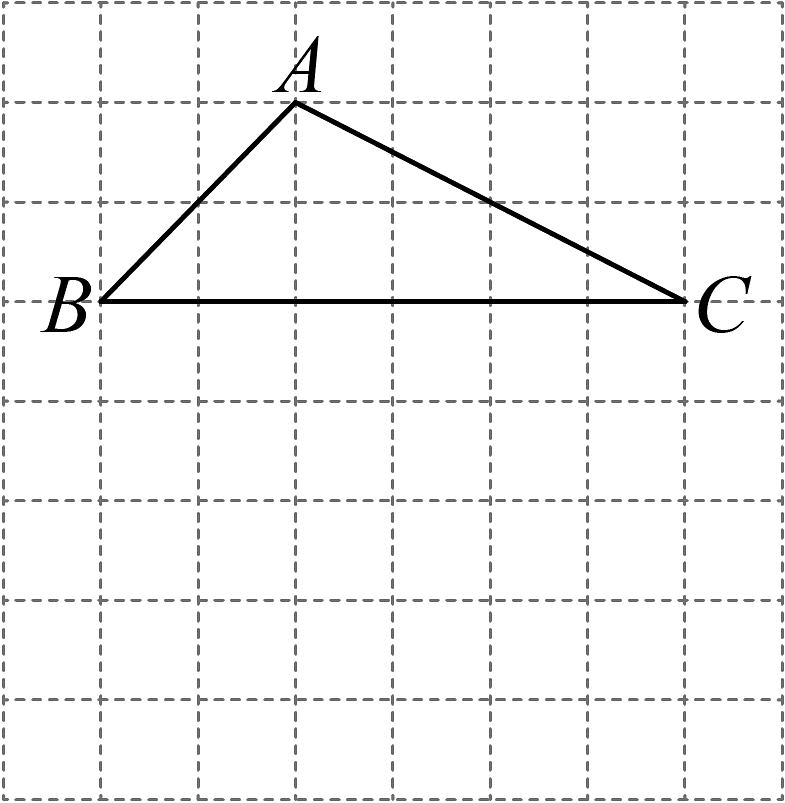 (1)、仅用一把无刻度直尺画出的外心点O.并用圆规面出外接圆;(2)、仅用一把无刻度直尺画弦 , 使得平分 .
(1)、仅用一把无刻度直尺画出的外心点O.并用圆规面出外接圆;(2)、仅用一把无刻度直尺画弦 , 使得平分 . -
7、如图,已知函数图象经过点 ,
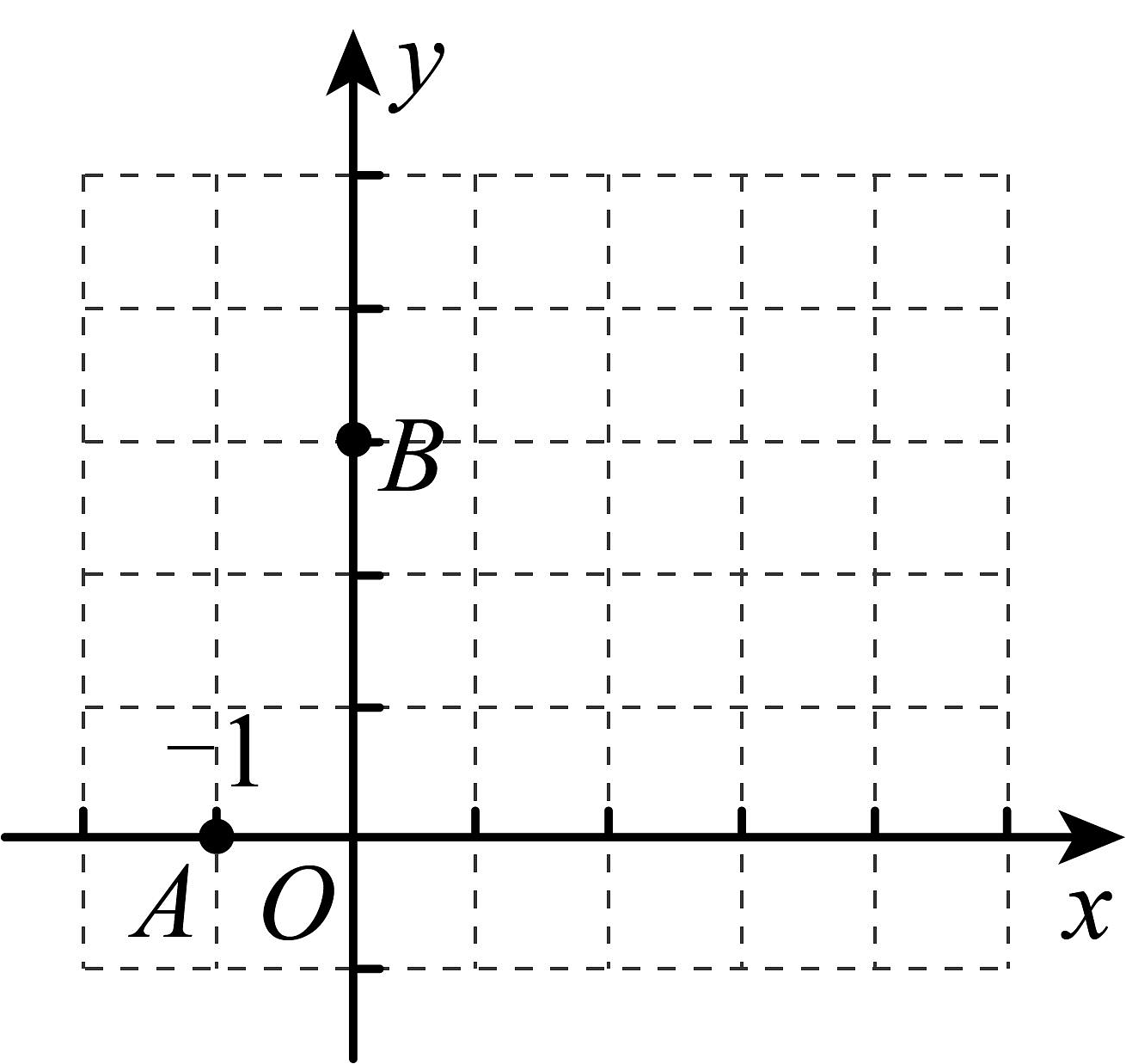 (1)、求b,c的值;(2)、在图中画出这个函数的图象;(不必列表)(3)、观察图像,当时,函数值y的取值范围是 .
(1)、求b,c的值;(2)、在图中画出这个函数的图象;(不必列表)(3)、观察图像,当时,函数值y的取值范围是 . -
8、如图,为的直径,且 , 点C为上半圆的一点,于点E,的角平分线交于点D,弦 , 那么的面积是 .

-
9、二次函数的部分对应值如下表:
x
…
0
1
3
5
…
y
…
7
0
7
…
则二次函数在时, .
-
10、若扇形的圆心角为 , 半径为6,则扇形的面积为 .
-
11、若 , , 为二次函数图象上的三点,则 , , 的大小关系为( )A、 B、 C、 D、
-
12、一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心到水面的距离是( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1 -
13、如图,四边形是的内接四边形,其中 , 则的度数为( )
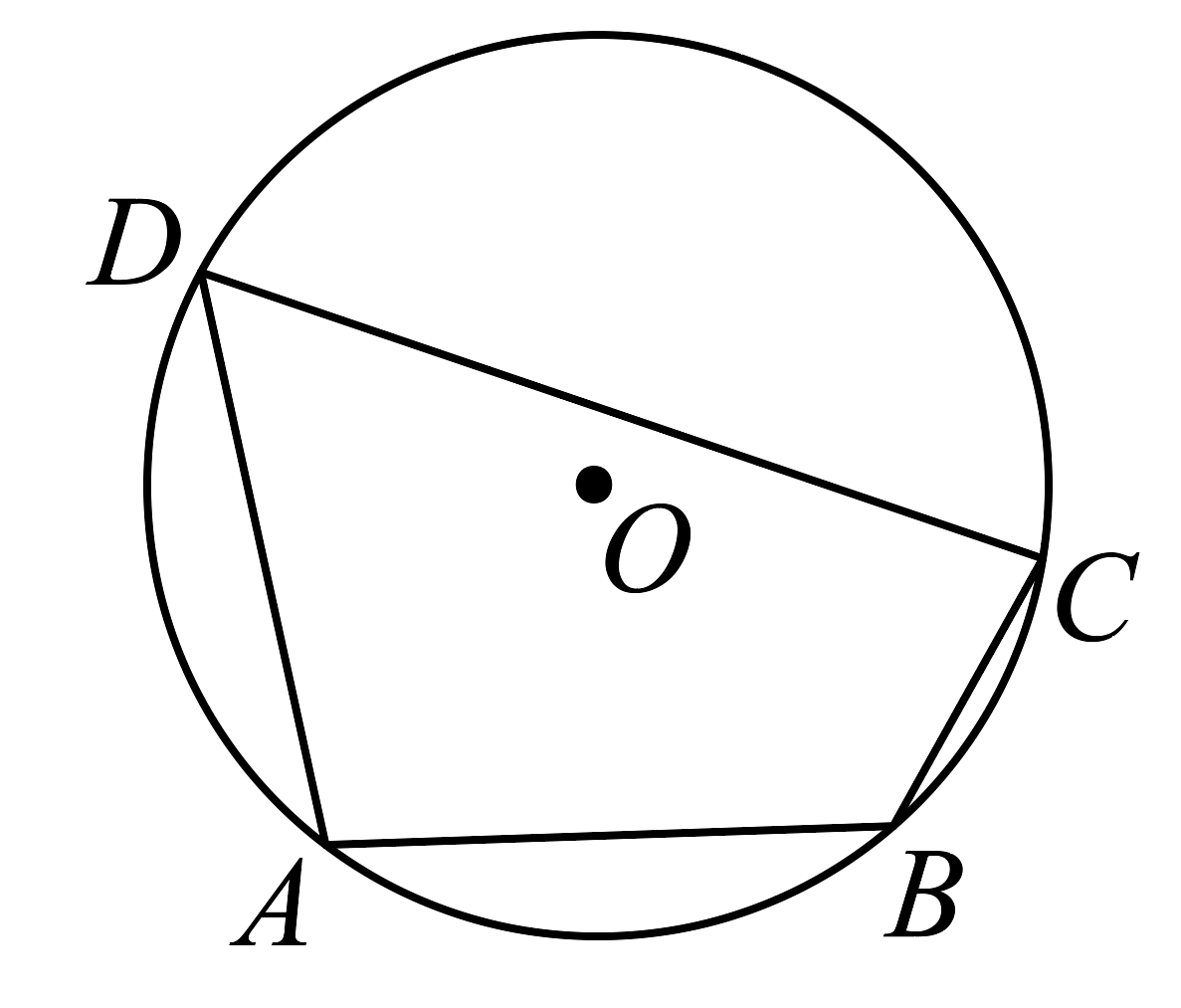 A、 B、 C、 D、
A、 B、 C、 D、 -
14、抛物线与y轴的交点坐标是( )A、 B、 C、 D、
-
15、如图,建筑工地上的塔吊上部设计成三角形结构,其中的数学原理是三角形的 .

-
16、已知二次函数的部分图象如图所示,则关于x的一元二次方程的解为 .

-
17、如图,在菱形中, , , 则( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、在中, , , , 将绕点逆时针旋转得到.
 (1)、 如图①,将绕点逆时针旋转 得到 , 连接 , 求的大小;(2)、 如图②,交于点 , 求证:点是的中点;(3)、 在绕点旋转一周的过程中,线段长度的最大值为.
(1)、 如图①,将绕点逆时针旋转 得到 , 连接 , 求的大小;(2)、 如图②,交于点 , 求证:点是的中点;(3)、 在绕点旋转一周的过程中,线段长度的最大值为. -
19、如图,在平面直角坐标系中,直线与轴、轴相交于 , 两点,动点在线段上,将线段绕点顺时针旋转 得到线段 , 此时点恰好落在直线上,过点作轴于点 .
 (1)、 求证:.(2)、 求点的坐标.(3)、 若点在轴上,点在直线上,是否存在以 , , , 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点坐标;若不存在,请说明理由.
(1)、 求证:.(2)、 求点的坐标.(3)、 若点在轴上,点在直线上,是否存在以 , , , 为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的点坐标;若不存在,请说明理由. -
20、如图①为便携式折叠椅,将其抽象成几何图形,如图②所示,测得 , , , , , ,已知.
 (1)、 求证:四边形是平行四边形;(2)、 求椅子最高点到地面的距离.
(1)、 求证:四边形是平行四边形;(2)、 求椅子最高点到地面的距离.