相关试卷

1、如图，在每个小正方形的边长均为1个单位长度的网格中， $△ A B C$ 的三个顶点都在其格点上，请用无刻度直尺作图，并保留作图痕迹．

(1)、在图1中，请以直线l为对称轴，画出与 $△ A B C$ 成轴对称的图形；

(2)、在图2中，请在直线l上找一点P，使得 $△ A B P$ 的周长最小．

查看解析
2、如图，在 $△ A B C$ 与 $△ B A D$ 中， $∠ C B A = ∠ D A B$ ， $∠ C = ∠ D$ ， $A C$ 与 $B D$ 交于点E．求证： $B E = A E$ ．

查看解析
3、等腰三角形的一个外角度数为100°，则顶角度数为．

查看解析
4、如图， $A C = A D$ ， $B C = B D$ ，则下列判断正确的是（）

A、 $C D$ 平分 $∠ A C B$ B、 $A B$ 平分 $∠ C A D$ C、 $C D$ 垂直平分 $A B$ D、 $A B$ 与 $C D$ 互相垂直平分

查看解析
5、如图，已知 $A B ∥ C D$ ， $A D ∥ B C$ ， $A C$ 与 $B D$ 交于点O，图中全等三角形有（　　）

A、1对 B、2对 C、3对 D、4对

查看解析
6、如图1，在等腰三角形 $A B C$ 中， $A B = A C$ ， $B D$ 是边 $A C$ 上的高线， $C D = 1, A D = 4$ ．点P是线段 $D A$ 上的一点，作 $P E ⊥ B C$ 于点E，连接 $D E$ ．

(1)、求 $A B =$ ________， $B C =$ ________；

(2)、①当点P在线段 $A D$ 上时，若 $△ C D E$ 是以 $C D$ 为腰的等腰三角形，请求出所有符合条件的 $D P$ 的长度．
②如图2，设 $P E$ 交直线 $A B$ 于点F，连接 $B P$ ，若 $A F = 3$ ，求 $B P$ 的长．

查看解析
7、（1）如图1， $△ A B C$ 是等边三角形，点D为 $B C$ 边上的一动点（点D不与B，C重合），以 $A D$ 为边在 $A D$ 右侧作等边 $△ A D E$ ，连接 $C E$ ，线段 $B D$ 与 $C E$ 的数量关系是_______， $∠ A C E =$ ________ $°$ ．
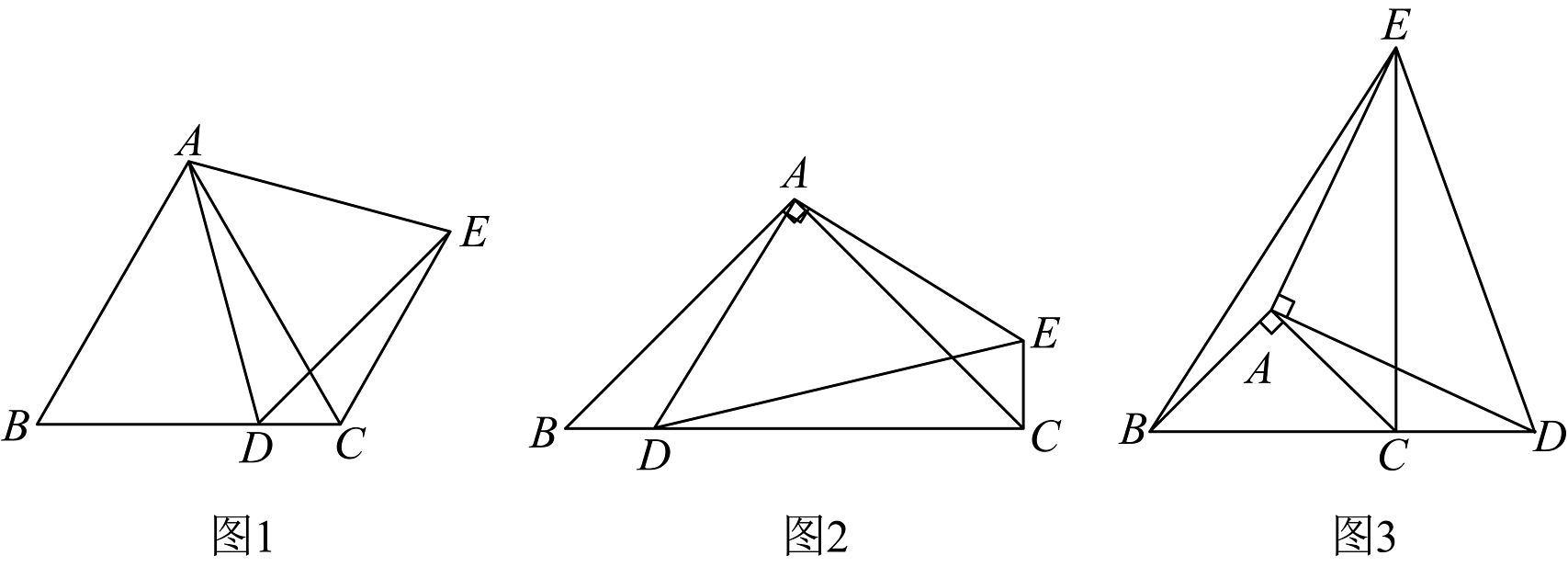
（2）如图2，在 $△ A B C$ 中， $∠ B A C = 90 °, A C = A B$ ，点D为 $B C$ 上的一动点（点D不与B，C重合），以 $A D$ 为边作等腰直角三角形 $A D E$ ， $∠ D A E = 90 °$ ，连接 $C E$ ，请求解下列问题并说明理由的度数．
① $∠ D C E$ 的度数；
②线段 $B D$ ， $C D$ ， $D E$ 之间的数量关系；
（3）如图3，在（2）的条件下，若D点在 $B C$ 的延长线上运动，以 $A D$ 为边作等腰直角 $△ A D E$ ， $∠ D A E = 90 °$ ，连接 $C E$ ， $B E$ ，若 $B E = 10, B C = 6$ ，请直接写出 $D E^{2}$ 的值．

查看解析
8、在 $△ A B C$ 中， $∠ C = 90 °, A C = 6, B C = 8$ ．回答下列问题：

(1)、由勾股定理，易知 $A B =$ ______；

(2)、如图，用尺规作图的方法作射线n交 $B C$ 边于P，求线段 $P C$ 的长．

查看解析
9、解不等式（组）：

(1)、 $3 x > 1 - 2 x$ ；

(2)、 $\frac{2 + x}{2} \leq \frac{2 x - 1}{3}$ ；

(3)、 $\{\begin{matrix} 2 x - 3 \geq 9 - x \\ 10 + 3 x < 2 x + 15 \end{matrix}$ ；

(4)、 $\{\begin{array}{l} \frac{1 - 5 x}{2} \geq \frac{3 x + 1}{3} - 1 \\ 3 (x - 1) \leq 5 (x + 1) - 2 \end{array}$

查看解析
10、如图，在△ $A B C$ 中， $A B = A C = 12$ ， $E$ ， $D$ 分别是 $A B$ ， $A C$ 上的点， $B E = 4$ ， $C D = 2$ ，且 $B D = C E$ ，则 $B D =$ ．

查看解析
11、如图，已知 $∠ B = 20 °$ ， $∠ C = 25 °$ ，若 $P M$ 和 $Q N$ 分别垂直平分 $A B$ 和 $A C$ ，则 $∠ P A Q =$ ．

查看解析
12、命题“若 $|m| = |n|$ ，则 $m = n$ ”的逆命题是．

查看解析
13、如图，在 $△ A B C$ 中， $A B = A C = 5, B C = 6$ ， D，E分别为线段 $A B$ ， $A C$ 上一点，且 $A D = A E$ ，连接 $B E$ 、 $C D$ 交于点G，延长 $A G$ 交 $B C$ 于点F．以下四个结论正确的是（）
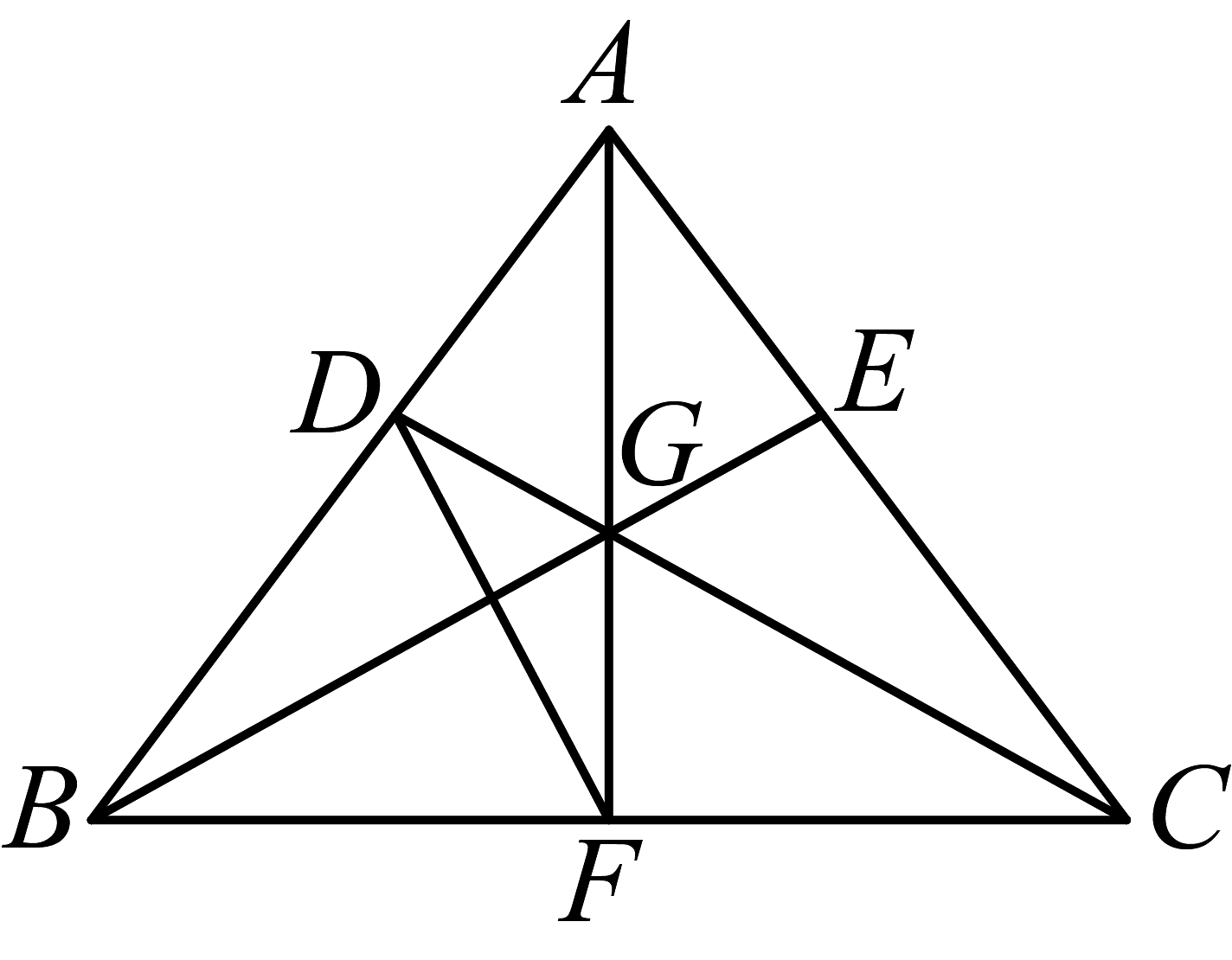
① $B F = C F$ ；
②若 $B E ⊥ A C$ ，则 $C F = D F$ ；
③连结 $E F$ ，若 $B E ⊥ A C$ ，则 $∠ D F E = 2 ∠ A B E$ ；
④若 $B E$ 平分 $∠ A B C$ ，则 $F G = \frac{3}{2}$

A、①②③ B、③④ C、①②④ D、①②③④

查看解析
14、关于 $x$ 的不等式组 $\{\begin{array}{l} x > m + 3 \\ 5 x - 2 < 4 x + 1 \end{array}$ 的整数解仅有5个，则 $m$ 的取值范围是（　　）

A、 $- 6 < m < - 5$ B、 $- 6 \leq m < - 5$ C、 $- 6 < m \leq - 5$ D、 $- 6 \leq m \leq - 5$

查看解析
15、如图所示的图案是由两个直角三角形和三个正方形组成的图形，其中一直角三角形的斜边和一直角边长分别是13，12，则阴影部分的面积是（）

A、25 B、16 C、50 D、41

查看解析
16、如图， $△ A B C$ 中，D为 $A B$ 中点，E在 $A C$ 上，且 $B E ⊥ A C$ ．若 $D E = 5$ ，则 $A B$ 的长度是（）

A、 $7.5$ B、8 C、 $10$ D、 $12$

查看解析
17、在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（）

A、 B、 C、 D、

查看解析
18、如图，在矩形 $A B C D$ 中， $A B = 3 cm$ ， $B C = 6 cm$ ．点 $P$ 从点 $D$ 出发向点 $A$ 运动，运动到点 $A$ 即停止；同时，点 $Q$ 从点 $B$ 出发向点 $C$ 运动，运动到点 $C$ 即停止，点 $P$ 、 $Q$ 的速度都是 $1 cm / s$ ．连接 $P Q$ 、 $A Q$ 、 $C P$ ．设点 $P$ 、 $Q$ 运动的时间为 $t s$ ．

(1)、当 $t =$ __________时，四边形 $A B Q P$ 是矩形；

(2)、当 $t =$ __________时，四边形 $A Q C P$ 是菱形；

(3)、是否存在某一时刻 $t$ 使得 $P Q ⊥ P C$ ，如果存在，请求出 $t$ 的值，如果不存在，请说明理由．

查看解析
19、解方程

(1)、 $x (x + 2) = 3 x + 2$

(2)、 $x (x + 1) = - 3 (x + 1)$ ；

查看解析
20、代数式 $- 3 x^{2} + 6 x - 4$ 的最大值是．

查看解析

上一页 406 407 408 409 410 下一页跳转