相关试卷

1、二次函数 $y = x^{2} - 4 x - 5$ 的图象的对称轴是( )

A、直线x=-2 B、直线x=2 C、直线x=-1 D、直线x=1

查看解析
2、如图，以AB 为直径作半圆⊙O，C是半圆的中点，P是 $⌢ B C$ 上一点.若AB=5 $\sqrt{2}$ ， PB=1，则PC 的长是.

查看解析
3、如图，⊙O是△ABC 的外接圆，∠ACB=120°，AB=2 $\sqrt{3}$ 求⊙O 的半径.

查看解析
4、如图，点A，B，C 在⊙O上，CD⊥OA，CE⊥OB，垂足分别为 D，E，若∠DCE=40°，求∠ACB 的度数.

查看解析
5、如图，AB 为⊙O 的直径，弦CD⊥AB，F 为BC 上的一点，DC，BF 的延长线交于点E.求证：∠EFC=∠BFD.

查看解析
6、如图①所示为一枚质地均匀的正四面体形状的骰子，每个面上分别标有数字1，2，3，4，如图②所示为一个正六边形棋盘.现通过掷骰子的方式玩跳棋游戏，规则如下：将这枚骰子掷出后，看骰子向上三个面(除底面外)的数字之和是几，就从图②中的点 A 开始沿着顺时针方向连续跳动几个顶点，第二次从第一次的终点处开始，按第一次的方法跳动.

(1)、随机掷一次骰子，棋子跳动到点 C 处的概率是.

(2)、随机掷两次骰子，用画树状图或列表的方法，求棋子最终跳动到点 C 处的概率.

查看解析
7、某博物馆展厅的俯视示意图如图①所示.嘉淇进入展厅后开始自由参观，每走到一个十字道口，她可能直行，也可能向左转或向右转，且这三种可能性均相同.

(1)、求嘉淇走到十字道口 A 时向北走的概率.

(2)、补全图②中的树状图，并分析嘉淇经过两个十字道口后向哪个方向参观的概率最大.

查看解析
8、有一枚质地均匀的骰子，其六个面上分别标有数字1，2，3，4，5，6.连续抛掷骰子两次，第一次正面朝上的数字作为十位数，第二次正面朝上的数字作为个位数，则这个两位数能被3整除的概率为.

查看解析
9、用甲、乙两个可自由转动的转盘(如图)做“配紫色”游戏：分别转动甲、乙两个转盘，若其中一个转出红色，另一个转出蓝色，即可配成紫色(若指针指在分界线上，则重转)，则配成紫色的概率为( )

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看解析
10、随着信息化的发展，二维码已经走进我们的日常生活，其图案主要由黑、白两种小正方形组成.现对由三个小正方形组成的“□□□”进行涂色，每个小正方形被随机地涂成黑色或白色，则恰好是两个黑色小正方形和一个白色小正方形的概率为( )

A、 $\frac{1}{3}$ B、 $\frac{3}{8}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看解析
11、某中学有7名学生的生日是10月 1 日，其中男生分别记为A₁ ， A₂ ， A₃ ， A₄ ，女生分别记为B₁ ， B₂ ， B₃.学校准备召开国庆联欢会，计划从这7名学生中抽取部分学生参与联欢会的访谈活动.

(1)、若任意抽取1名学生，则抽取的学生为女生的概率是.

(2)、若先从男生中任意抽取1名，再从女生中任意抽取1名，求抽得的2 名学生中至少有1名是A₁或B₁的概率(请用画树状图或列表的方法写出分析过程).

查看解析
12、重庆是一座魔幻都市，有着丰富的旅游资源.甲、乙两人相约来重庆旅游，两人分别从A，B，C三个景点中随机选择一个景点游览，则甲、乙两人同时选择景点B 的概率为.

查看解析
13、如图，每个转盘被分成面积相等的几个扇形，同时转动甲、乙两个转盘，则两个转盘停止后，指针(若在分隔线上，则重新转动，直至转到其中一块区域)都不落在“1”区域的概率是( )

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{5}{6}$ D、 $\frac{1}{6}$

查看解析
14、一个不透明的盒子里装有一个红球、一个白球和一个绿球，这些球除颜色外其他都相同.从中随机摸出一个球，记下颜色后不放回，再从中随机摸出一个球，则两次摸到的球恰好有一个红球的概率是( )

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{4}{9}$ D、 $\frac{5}{9}$

查看解析
15、如图，在平面直角坐标系中，已知 $A (0, a)$ ， $B (b, 0)$ ， b满足 $| a - 2 | + {(b - 3)}^{2} = 0$ ．

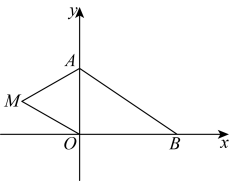(1)、求a ， b的值；

(2)、如果在第二象限内有一点 $M (m, 1)$ ，请用含m的式子表示四边形 $A B O M$ 的面积；

(3)、在（2）条件下，当 $m = - \frac{3}{2}$ 时，在坐标轴的负半轴上是否存在点N ，使得四边形 $A B O M$ 的面积与 $△ A B N$ 的面积相等？若存在，求出点N的坐标，请说明理由．

查看解析
16、如图所示，在平面直角坐标系中，点 $A$ ， $B$ 的坐标分别为 $A (- 2, 0)$ ， $B (a, 0)$ ，其中 $A$ 在 $B$ 的左侧且 $A B = 6$ ，点 $C$ 的坐标为 $(0, 3)$ ．

(1)、求 $a$ 的值及 $S_{△ A B C}$ ；

(2)、若点 $M$ 在 $x$ 轴的正半轴上，且 $S_{△ A C M} = \frac{1}{3} S_{△ A B C}$ ，试求点 $M$ 的坐标．

查看解析
17、已知点 $P (a - 1, 2 a + 6)$ ，分别根据下列条件求出点 $P$ 的坐标．

(1)、点 $P$ 在 $x$ 轴上；

(2)、点 $P$ 在 $y$ 轴上；

(3)、点 $Q$ 的坐标为 $(1, 5)$ ，直线 $P Q ∥ y$ 轴．

查看解析
18、在平面直角坐标系中，点P从原点O出发，速度为每秒1个单位长度，且点P只能向上或向右运动，请回答下列问题：

(1)、将表格填写完整：
点P出发时间
可得到整数点的坐标
可得到整数点的个数
1秒
$(0 ， 1)$ ， $(1 ， 0)$
2
2秒
$(1 ， 1)$ ， $(2 ， 0)$ ， $(0 ， 2)$
3
3秒
4

(2)、当点P从点O出发11秒时，可得到的整数点的个数是．

(3)、当点P从点O出发秒时，可得到整数点 $(28 ， 8)$ ．

查看解析
19、在平面直角坐标系中，给出如下定义：点P到x轴、y轴的距离的较大值称为点P的“长距”，点Q到x轴、y轴的距离相等时，称点Q为“完美点”．

(1)、点 $A (2, - 4)$ 的“长距”是；点 $B (- 9, 7)$ 的“长距”是；

(2)、若点 $C (2 a + 1, - 3)$ 是“完美点”，求a的值；

(3)、若点 $D (- 2, 3 b - 2)$ 的长距为4，且点D在第二象限内，点E的坐标为 $(5, 2 b - 9)$ ，请判断点E是否为“完美点”，并说明理由．

查看解析
20、在平面直角坐标系中， $△ A B C$ 的三个顶点坐标分别为 $A (2, 3)$ ， $B (4, 0)$ ， $C (3, - 2)$ ，直线 $m$ 上所有点的横坐标都是 $1$ ．

(1)、在平面直角坐标系中，作出 $△ A B C$ 关于直线 $m$ 对称的 $△ D E F$ ，其中点 $A$ ，点 $B$ ，点 $C$ 的对应点分别是点 $D$ ，点 $E$ ，点 $F$ ；

(2)、直接写出点 $D$ ，点 $E$ ，点 $F$ 的坐标：点 $D$ （，），点 $E$ （，），点 $F$ （，）；

(3)、直接写出 $A D$ 的长度： $A D =$ ．

查看解析

上一页 402 403 404 405 406 下一页跳转

点P出发时间	可得到整数点的坐标	可得到整数点的个数
1秒	$(0 ， 1)$ ， $(1 ， 0)$	2
2秒	$(1 ， 1)$ ， $(2 ， 0)$ ， $(0 ， 2)$	3
3秒		4