-
1、在0,1,2,3,4,5这六个数字中任意选取三个数字,组成一个三位递升数(个位数字大于十位数字,十位数字大于百位数字),则这个三位数能被3整除的概率为( )A、 B、 C、 D、
-
2、如图,在三条横线和三条竖线组成的图形中,任选两条横线和两条竖线都可以围成一个矩形,从这些矩形中任选一个,则所选矩形含点 A 的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、同时闭合如图所示的电路图的两个开关,能形成闭合电路的概率为( )
 A、 B、 C、 D、1
A、 B、 C、 D、1 -
4、如图,将1个棱长为3的正方体表面涂色,再把它分割成棱长为1的小正方体,从中任取1个小正方体,则取得的小正方体恰好有2个面涂色的概率为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、下列转盘分别被分成2,4,5,6个面积相等的扇形,任意转动这4个转盘各1次.已知某转盘停止转动时,指针落在涂色区域的概率为 , 则对应的转盘是( )A、
 B、
B、 C、
C、 D、
D、
-
6、下列说法中,合理的是( )A、小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是 B、抛掷一枚质地均匀的正六面体骰子,出现6朝上的概率是 的意思是每6次就有1次掷得6 朝上 C、若某彩票的中奖概率是2%,则买100张彩票一定会有2张中奖 D、在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51
-
7、下列事件发生的概率为0的是( )A、汽车累计行驶5000km,从未出现故障 B、任取一个实数x,都有 C、画一个三角形,使其三边的长分别为8cm,6cm,2cm D、抛掷一枚质地均匀且六个面上分别刻有1到6的点数的正方体骰子,朝上一面的点数为6
-
8、音乐课上老师带领同学们玩“抽音符、唱音符”的游戏,老师手中的卡片如图所示(叠放的为相同卡片),卡片背面相同,洗匀后背面朝上,嘉嘉从中抽取一张卡片,抽到的卡片可能性最大的是( )
 A、C(哆)音符 B、D(来)音符 C、E(咪)音符 D、以上都不对
A、C(哆)音符 B、D(来)音符 C、E(咪)音符 D、以上都不对 -
9、若“一个不透明的袋中装有三个球,其上面分别标有1,2,x这三个号码,这些球除号码外都相同,搅匀后任意摸出一个球,摸出的球上面的号码小于5”是必然事件,则x 的值可能是( )A、4 B、5 C、6 D、7
-
10、黄金分割被广泛应用在建筑、艺术等领域,我国早在战国时期就已知道并能应用黄金分割.中国澳门发行的邮票小型张《科学与科技——黄金比例》(如图1)就是用黄金分割比作为主题设计的.
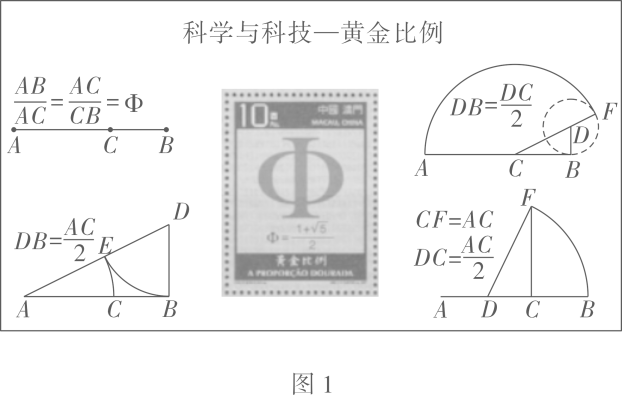
【阅读观察】
材料1:黄金分割点的定义
如图2,若线段上的点满足 , 则点称作线段的黄金分割点,其中的比直称作黄金分割比 , 而的比值为与互为倒数.

材料2:黄金分割点的作法(借助尺规作图可以用不同方法确定图2中线段的黄金分割点)
方法1:如图3,①过点作;
②在直线上截取 , 连接;
③在上截取;
④在上截取点即为所求.
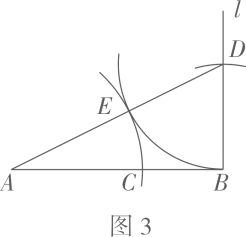
方法2:如图4,
①以为边作正方形;
②取中点 , 连接;
③以点为圆心,为半径作圆弧,与的延长线交于点;
④以为边在一侧作正方形交于点 , 可得 . 点即为所求.
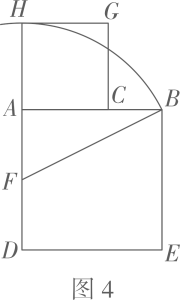
【思考探究】
(1)、说明图3中;(2)、用不同于(1)的方法,说明图4中 .(3)、【迁移拓展】如图5,作圆内接正五边形:
①作的两条互相垂直的半径和 , 取的中点 , 连接;
②作的平分线,交于点;
③过点作的垂线,交于点 , 连接;
④截取 , 连接 . 五边形即为所求.

若 , 根据以上作法,证明: .
-
11、如图,在平面直角坐标系中,二次函数与正比例函数的图象都经过点 , 点为二次函数图象上点与点之间的一点,过点作轴的垂线,交于点 , 交轴于点 .
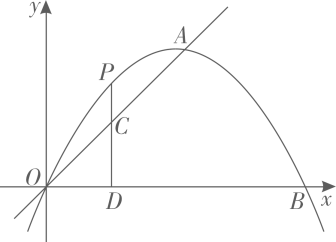 (1)、若点为该二次函数的顶点,
(1)、若点为该二次函数的顶点,①求二次函数的表达式;
②求线段长度的最大值.
(2)、若该二次函数与轴的一交点为 , 且 , 求的取值范围. -
12、图1是某摩天轮的实景图.摩天轮可视作半径为50米的 , 其上的某个座舱可视作上的点 , 座舱距离地面的最低高度为10米,地面上的观察点到点的距离为80米,平面示意图如图2所示.
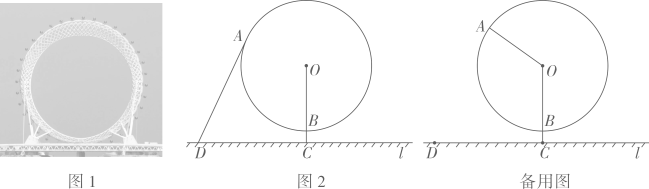 (1)、当视线与相切时,求点处的座舱到地面的距离.(2)、已知摩天轮匀速转动一周需要30分钟,当座舱距离地面不低于85米时,在座舱中观赏风景的体验最佳.点处的座舱随摩天轮匀速转动一周的过程中,求该座舱中乘客最佳观赏风景的时长,并求这段时间内该座舱经过的圆弧的长.
(1)、当视线与相切时,求点处的座舱到地面的距离.(2)、已知摩天轮匀速转动一周需要30分钟,当座舱距离地面不低于85米时,在座舱中观赏风景的体验最佳.点处的座舱随摩天轮匀速转动一周的过程中,求该座舱中乘客最佳观赏风景的时长,并求这段时间内该座舱经过的圆弧的长.(以上结果均保留小数点后一位数字,参考数据: ,
-
13、 为培育玉米新品种,研究人员对某生长期试验田和对照田中的玉米株高进行抽样调查并作比较研究,分别随机选取40株玉米测量其株高,整理数据如下.
【数据收集】
试验田玉米株高(cm)
对照田玉米株高(cm)
56,43,51,52,45,55,46,55,46,51,54,54,48,55,48,49,51,50,48,49,49,51,46,51,43,51,52,47,54,49,55,46,48,45,53,47,43,54,43,56.
41,52,40,48,60,40,44,54,44,45,46,55,48,40,48,54,50,50,52,52,52,60,52,52,40,54,48,40,54,54,55,46,56,40,60,60,56,57,52,60.
【数据整理】
把数据分为5组,制成如下频数分布表.(用表示株高,)
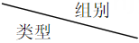
A
B
C
D
E
试验田玉米株频数
4
8
15
11
2
对照田玉米株频数
7
5
6
14
8
(1)、你赞同下面小亮的观点吗?请说明你的理由. (2)、【数据描述】
(2)、【数据描述】根据频数分布表分别制作试验田频数直方图和对照田扇形统计图.

补全试验田频数直方图并计算对照田D组所占圆心角的度数;
(3)、已知此生长期的玉米株高满足为长势良好.比较以上两个统计图,写出图中蕴含的信息.(一条即可)(4)、【数据分析】对收集的数据进行分析,得出的统计量如下表:
统计量
中位数
众数
平均数
方差
试验田
49.5
51
49.73
15.10
对照田
52
52
50.28
40.05
根据(3)中“长势良好”的标准及以上信息,评估此生长期试验田的玉米生长情况.
-
14、如图,在△ABC中,点分别是边的中点,与相交于点 , 连接 . 证明:
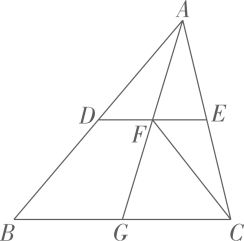 (1)、;(2)、△ADF≌△CFE .
(1)、;(2)、△ADF≌△CFE . -
15、某企业为提高生产效率,采购了相同数量的型、型两种智能机器人,购买型机器人的总费用为90万元,购买型机器人的总费用为60万元,型机器人单价比型机器人单价低3万元.(1)、求型、型两种机器人的单价;(2)、该企业计划从采购的这批机器人中选择10台配备到某生产线,要求两种型号的机器人各至少配备1台,且购买这10台机器人的总费用不超过70万元.求出所有配备方案.
-
16、 如图,已知菱形的顶点在方格纸的格点上,其中的坐标分别为(0,1), . 该菱形经过中心对称得到它右侧的菱形(顶点均在格点上).
 (1)、画出平面直角坐标系,并写出对称中心的坐标和点的对应点的坐标;(2)、将菱形平移,使点的对应点为点 , 画出平移后的菱形.
(1)、画出平面直角坐标系,并写出对称中心的坐标和点的对应点的坐标;(2)、将菱形平移,使点的对应点为点 , 画出平移后的菱形. -
17、(1)、先化简,再求值: , 其中满足 .(2)、解方程组:
-
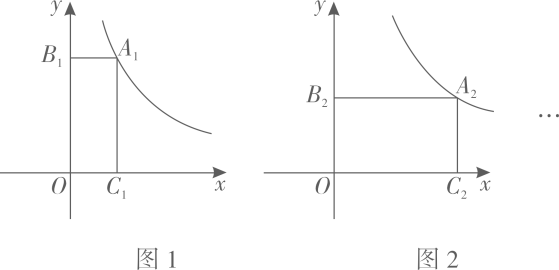
18、如图1,点是函数图象上任意一点,过向轴作垂线交轴于点 , 向轴作垂线交轴于点 , 矩形的周长 , 当时,有最小值4;如图2,点是函数图象上任意一点,同样作矩形 , 它的周长 , 同理得的最小值为;点是函数(为正整数)图象上任意一点,作矩形 , 它的周长为 , 则的最小值为 .
-
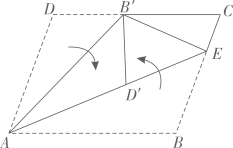
19、如图,在□中,点在边上.将沿折叠,点的对应点恰好落在边上;将△ADB'沿折叠,点的对应点恰好落在上.若 , 则 . (用含的式子表示)
-
20、如图,圆锥的底面圆心为 , 顶点为 , 母线长为4,母线与高的夹角为 , 那么圆锥侧面展开图的面积为 .
