相关试卷
- 浙教版数学八年级上册4.1.2 平面直角坐标系 同步分层练习
- 浙教版数学八年级上册4.1.1 平面直角坐标系 同步分层练习
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测提升卷
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测培优卷
- 浙教版数学八年级上册第3章 一元一次不等式 单元检测基础卷
- 北师大版数学八年级上册单元分层检测卷第二章 《实数》B卷
- 浙教版数学八年级上册3.5 一元一次不等式组 同步分层练习
- 湘教版数学七年级上册 3.3 一元一次方程的解法 第二课时 同步分层练习
- 湘教版数学 七年级上册 3.3 一元一次方程的解法 第一课时 同步分层练习
- 湘教版数学七年级上册 3.2 等式的基本性质 第三课时 同步分层练习
-
1、一条排水管的截面如图所示, 已知排水管的半径 , 水面宽 , 则截面圆心到水面的距离是( )
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1 -
2、如图,四边形是的内接四边形,其中 , 则的度数为( )
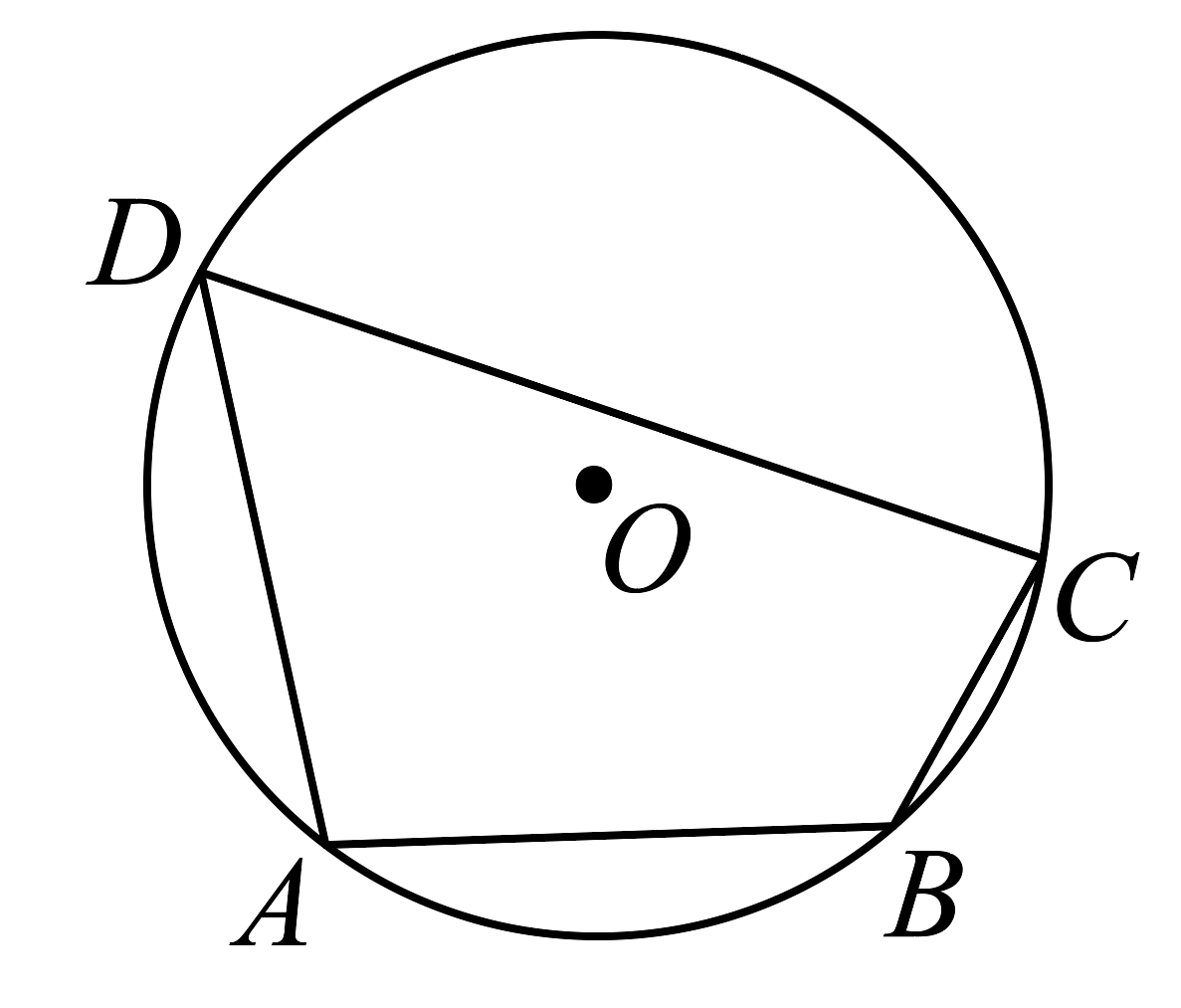 A、 B、 C、 D、
A、 B、 C、 D、 -
3、抛物线与y轴的交点坐标是( )A、 B、 C、 D、
-
4、在中, , , , 将绕点逆时针旋转得到.
 (1)、 如图①,将绕点逆时针旋转 得到 , 连接 , 求的大小;(2)、 如图②,交于点 , 求证:点是的中点;(3)、 在绕点旋转一周的过程中,线段长度的最大值为.
(1)、 如图①,将绕点逆时针旋转 得到 , 连接 , 求的大小;(2)、 如图②,交于点 , 求证:点是的中点;(3)、 在绕点旋转一周的过程中,线段长度的最大值为. -
5、如图,的对角线 , 相交于点 , 过点且与 , 分别相交于点 , , 连接.
 (1)、 求证:;(2)、 若 , 的周长是10,求的周长.
(1)、 求证:;(2)、 若 , 的周长是10,求的周长. -
6、如图,在中,点 , 分别在 , 的延长线上,直线与对角线平行,交于点 , 交于点.
 (1)、 求证:;(2)、 猜想与的数量关系,并说明理由.
(1)、 求证:;(2)、 猜想与的数量关系,并说明理由. -
7、如图,在中, ,在边上截取 , 连接 , 过点作于点 , 是边的中点,连接.若 , , 求的长度.

-
8、如图,点 , 为定点,直线 , 是上一动点,点 , 分别为 , 的中点,对于下列各值,其中会随着点的移动而发生变化的是(填序号).①线段 的长;的周长;的面积;④直线 与 之间的距离;的大小.

-
9、如图,小宇将一张平行四边形纸片折叠,使点落在长边上的处,并得到折痕 , 小宇测得长边 , 则四边形的周长为.

-
10、教材P142习题 如图,在四边形中, , , , 分别是 , , 的中点,若 , ,则 .

-
11、如图,在四边形中, , 是上一点,连接并延长,交的延长线于点 , 请你只添加一个条件: , 使得四边形为平行四边形.

-
12、如图,若直线 , , 在直线上, , 在直线上, , , , 的面积为6,则直线与之间的距离为.

-
13、如果从一个多边形的一个顶点出发作它的对角线,最多能将多边形分成7个三角形,那么这个多边形是边形.
-
14、如图,平行四边形的对角线 , 相交于点 , , , 是的中点,连接 , .下列结论: ;平分;;.其中结论正确的序号是( )
 A、①② B、②③④ C、①②③ D、①③④
A、①② B、②③④ C、①②③ D、①③④ -
15、在等边三角形中, , 射线 , 点从点出发,沿射线以的速度运动,同时点从点出发,沿射线以的速度运动,设运动时间为 , 当为多少时,以 , , , 为顶点的四边形是平行四边形?( )
 A、2 B、3 C、6 D、2或6
A、2 B、3 C、6 D、2或6 -
16、如图,的对角线 , 相交于点 , 的平分线与边相交于点 , 是的中点,若 , , 则的长为( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
17、如图所示,在平面直角坐标系中,平行四边形的顶点 , 的坐标分别是 , , , 则顶点的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
18、如图,在四边形中,点 , , , 分别是线段 , , , 的中点,则四边形的周长( )
 A、只与 , 的长有关 B、只与 , 的长有关 C、只与 , 的长有关 D、与四边形各边的长都有关
A、只与 , 的长有关 B、只与 , 的长有关 C、只与 , 的长有关 D、与四边形各边的长都有关 -
19、已知一个多边形的内角和是外角和的3倍,则此多边形的边数为( )A、8 B、7 C、6 D、5
-
20、如图,在中,是的平分线交于点 , 且 , 的周长是26,则( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6