-
1、下列计算正确的是( ).A、 B、 C、 D、
-
2、下列各式 , , , , , 其中分式共有( ).A、1个 B、2个 C、3个 D、4个
-
3、下列说法正确的是( )A、形状相同的两个图形全等 B、完全重合的两个图形全等 C、面积相等的两个图形全等 D、所有的等边三角形全等
-
4、若二次函数的图象经过原点,则为( )A、0 B、2 C、 D、
-
5、下列图形中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
6、已知代数式;;(1)、求;(2)、当时,求的值;(3)、若的值与的x取值无关,求y的值,
-
7、如图,三角形在网格图中,已知点 , .
 (1)、在图中建立平面直角坐标系;(2)、将三角形平移,使点平移到点的位置,点平移后的对应点分别为 , , 画出三角形;(3)、若点是三角形边上一点,经过第(2)问中的平移后,点对应的点的坐标是_____.
(1)、在图中建立平面直角坐标系;(2)、将三角形平移,使点平移到点的位置,点平移后的对应点分别为 , , 画出三角形;(3)、若点是三角形边上一点,经过第(2)问中的平移后,点对应的点的坐标是_____. -
8、已知的算术平方根是的立方根是是的整数部分,求的平方根.
-
9、定义:有一组对角互补的四边形叫做互补四边形.
 (1)、互补四边形中,若 , 求的度数;(2)、如图 , 在四边形中,平分 , , . 求证:四边形是互补四边形;(3)、如图 , 互补四边形中, , , 点 , 分别是边 , 的动点,且 , 周长是否变化?若不变,请求出不变的值;若有变化,说明理由;(4)、如图 , 互补四边形中, , , , 将纸片先沿直线对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为的平行四边形,求的长.
(1)、互补四边形中,若 , 求的度数;(2)、如图 , 在四边形中,平分 , , . 求证:四边形是互补四边形;(3)、如图 , 互补四边形中, , , 点 , 分别是边 , 的动点,且 , 周长是否变化?若不变,请求出不变的值;若有变化,说明理由;(4)、如图 , 互补四边形中, , , , 将纸片先沿直线对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为的平行四边形,求的长. -
10、数轴上点与点之间的距离记为: . 如图,在数轴上 , , 三点对应的数分别为 , , , 已知 , , 且点 , 点到点的距离相等,即 .
 (1)、填空:点对应的数为 ;(2)、若点从点出发,以个单位/秒的速度沿数轴向右移动,同时点从点出发,以个单位/秒的速度向右移动,在点 , 移动的同时点从点出发,以个单位/秒的速度沿数轴向右移动,设移动时间为秒.
(1)、填空:点对应的数为 ;(2)、若点从点出发,以个单位/秒的速度沿数轴向右移动,同时点从点出发,以个单位/秒的速度向右移动,在点 , 移动的同时点从点出发,以个单位/秒的速度沿数轴向右移动,设移动时间为秒.①若点到的距离是点到的距离的两倍,我们就称点是的“幸福点”.当点是的“幸福点”时,求此时点对应的数;
②在三个点移动的过程中,或在某种条件下是否会为定值,请分析并说明理由.
-
11、已知 .(1)、求;(2)、求;(3)、如果 , 那么C的表达式是什么?
-
12、底面积为 , 高为的圆柱形容器内有若干水,水位高度为 , 现将一个边长为的立方体铁块水平放入容器底部,立方体完全沉没入水中(如图甲).再将一个边长为的立方体铁块水平放在第一个立方体上面,若第二个立方体只有一半没入水中(如图乙).此时水位高度为 , 若 , 则 .

-
13、若是方程的解,则代数式的值为 .
-
14、多项式的一次项是 .
-
15、比较大小:0 , , . (填“”,“”号)
-
16、若用表示任意正实数的整数部分,例如: , , , 则式子的值为( )(式子中的“”,“”依次相间)A、22 B、 C、23 D、
-
17、如图, 数轴上两点分别对应实数 , 则化简的结果是( )
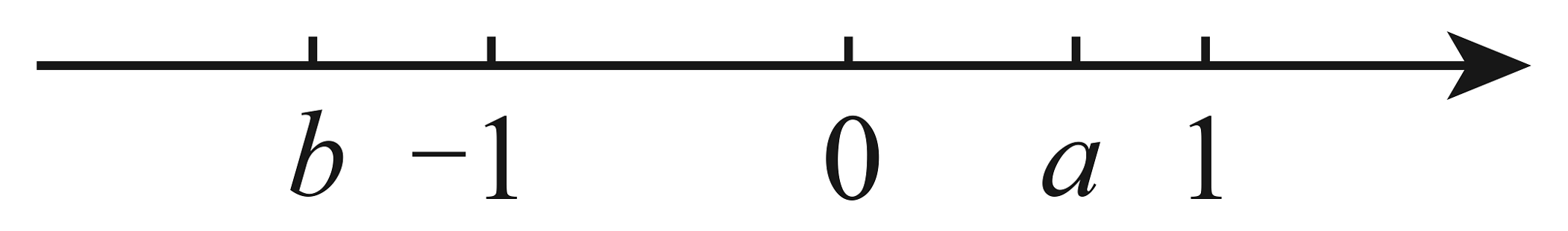 A、 B、 C、 D、
A、 B、 C、 D、 -
18、如图,每个小正方形的边长为1, , , 是小正方形的顶点,则的度数为 .
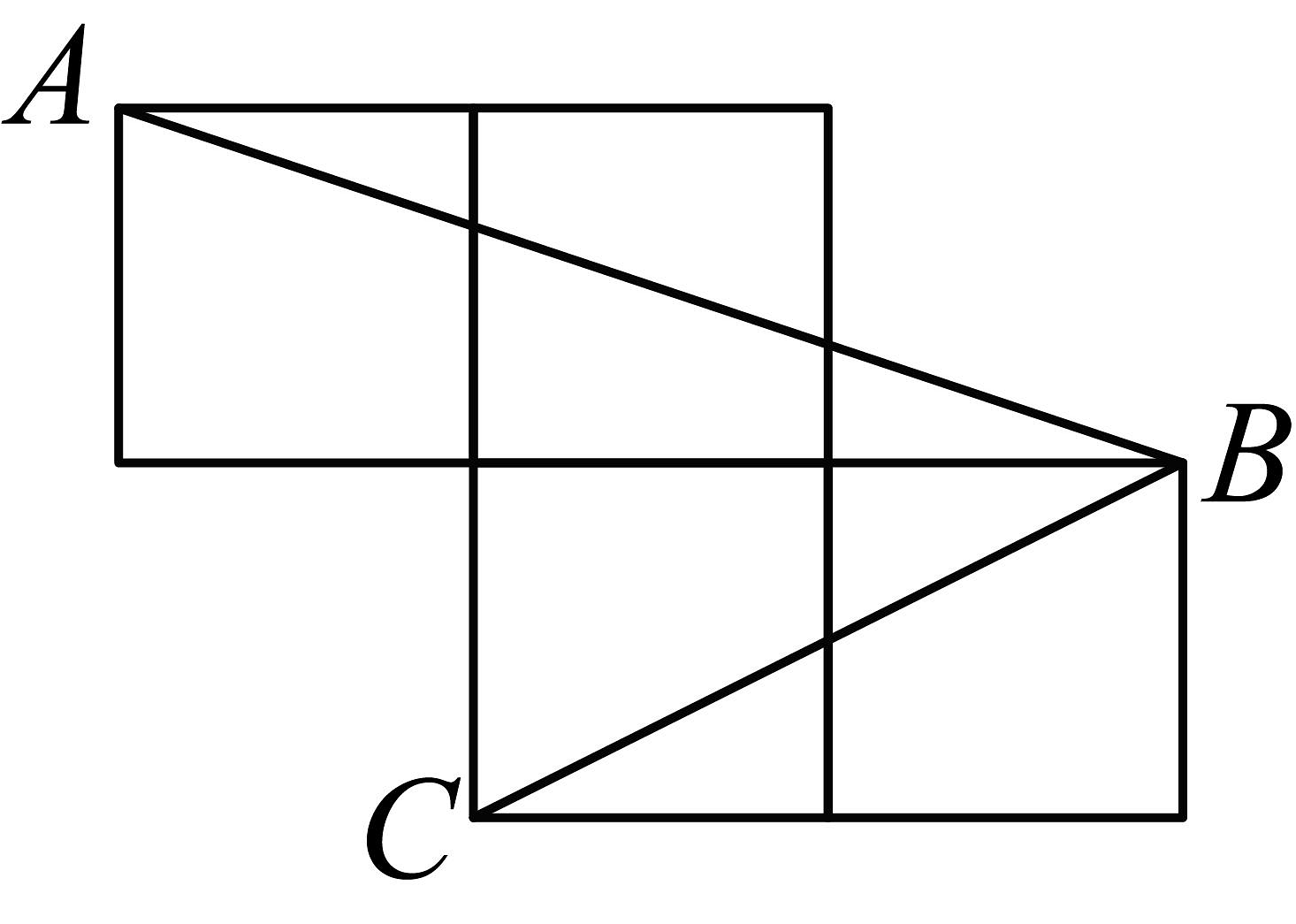
-
19、如图,在一条不完整的数轴上从左到右依次有点A,B,C三个点,其中点A到点B的距离为3,点B到点C的距离为8,设点A,B,C所对应的数的和是m.
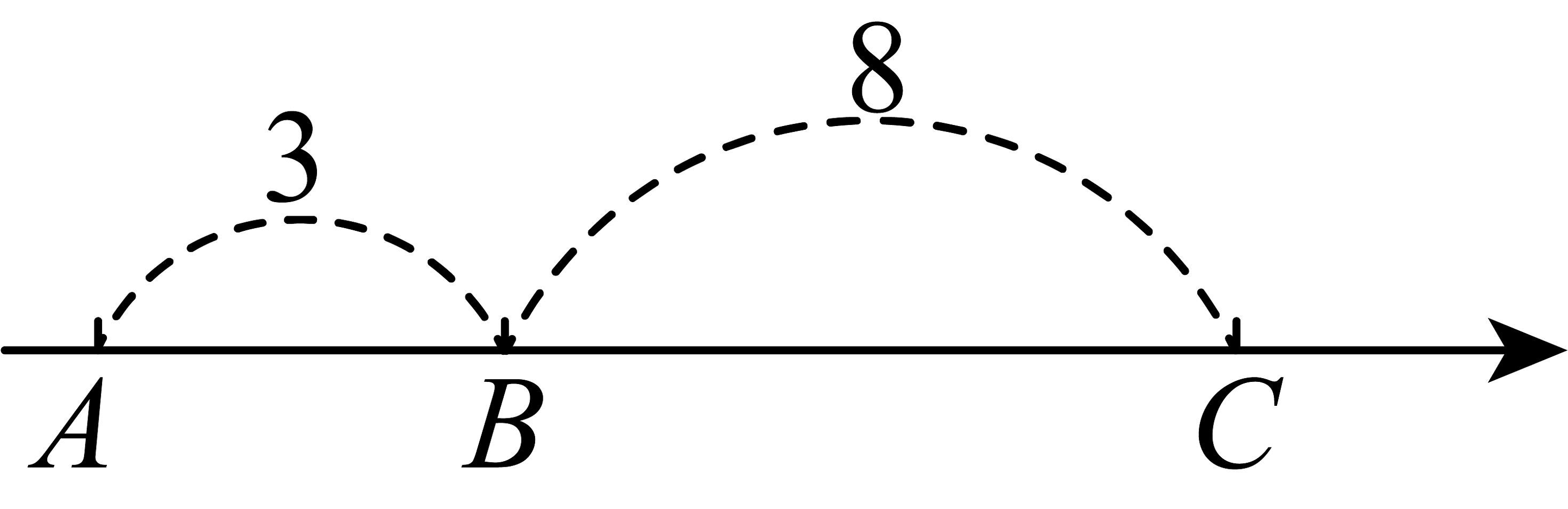 (1)、若A表示的数是 , 则数轴上点B所表示的数为: ;(2)、若以B为原点,求m的值;(3)、若C表示的数是8,将数轴折叠,使点A与点C重合,求折叠后与点B重合的点表示的数.
(1)、若A表示的数是 , 则数轴上点B所表示的数为: ;(2)、若以B为原点,求m的值;(3)、若C表示的数是8,将数轴折叠,使点A与点C重合,求折叠后与点B重合的点表示的数. -
20、如图是一个正方体的平面展开图,若该正方体相对面上的两个数和为5,回答下列问题:
 (1)、 , , ;(2)、求的值.
(1)、 , , ;(2)、求的值.