-
1、 由若干大小相同的小立方块搭成的几何体如图所示,则该几何体的主视图为( )
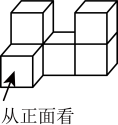 A、
A、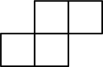 B、
B、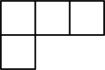 C、
C、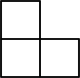 D、
D、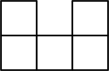
-
2、 近年来我国电影行业发展迅速,电影《哪吒之魔童闹海》风靡全球,据统计,截至2025年5月底,其票房达到约150亿元.数字15000000000用科学记数法表示为( )A、 B、 C、 D、
-
3、 某学校开展了“共走平安路”交通安全主题教育活动.以下交通标识图形既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4、 -2025的绝对值是( )A、2025 B、 C、-2025 D、
-
5、定义:满足不等式的实数x的所有取值的全体叫作闭区间,表示为 , 对于一个函数,如果它的自变量与函数值y满足:当时,有 , 我们称此函数是闭区间上的“闭函数”.如函数 , 当时,;当时, , 即当时,有 , 所以函数是闭区间上的“闭函数”.根据定义解答下列问题:(1)、试判断函数是不是闭区间上的“闭函数”并说明理由;(2)、若一次函数是闭区间上的“闭函数”,求它的表达式;(3)、若函数( , )是闭区间()上的“闭函数”,求的取值范围.
-
6、如图,在矩形中,为上一点, , , 过点作 , 交于 , 交于 , .
 (1)、求;(2)、求;(3)、若上存在点 , 使得 , 求 .
(1)、求;(2)、求;(3)、若上存在点 , 使得 , 求 . -
7、关于x的一元二次方程 .(1)、如果方程有实数根,求k的取值范围;(2)、如果 , 是这个方程的两个根,且 , 求k的值.
-
8、年“奔跑吧·少年”道县青少年篮球赛正如火如荼的在道县文体公园体育馆进行,若初中组采用单循环赛制(每两个球队之间都要进行一场比赛),则共要比赛场.试求初中组共有多少支球队参加比赛.
-
9、某蔬菜生产基地用装有恒温系统的大棚栽培一种新品,如图是某天恒温系统从开始到关闭及关闭后,大棚里温度随时间变化的函数图象,其中段是恒温阶段, 段是双曲线的一部分,请根据图中信息解答下列问题:
 (1)、求k的值;(2)、恒温系统在一天内保持大棚内温度不低于的时间有多少小时?
(1)、求k的值;(2)、恒温系统在一天内保持大棚内温度不低于的时间有多少小时? -
10、定义新运算:对于任意实数a,b,c,d有 , 其中等式右边是常用的乘法和减法运算.如: .(1)、求的值;(2)、已知关于x的方程的一个根为2,求m的值.
-
11、用合适的方法解方程.(1)、;(2)、 .
-
12、若m是一元二次方程的一个根,则的值为 .
-
13、若三角形三边之比为 , 与它相似的三角形的最长边为 , 则此三角形周长为 .
-
14、如图,支点O是跷跷板的中点,若支柱m,当跷跷板的一端B完全着地时,跷跷板的另一端A离地面的高度为m.

-
15、一元二次方程化为一般形式是 .
-
16、若 , 则 .
-
17、我国古代数学家曾经研究过一元二次方程的几何解法,三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载:构造如图所示的大正方形 , 它由四个全等的矩形和中间一个小正方形组成,以方程 , 即为例说明,构造如图中大正方形的面积是 , 同时它又等于四个矩形的面积加上中间小正方形的面积,即 , 解得 , 小明用此方法解关于x的方程时,构造出同样的图形,已知矩形的面积为16,则大正方形的面积S和n的值分别为( )
 A、 , B、 , C、 , D、 ,
A、 , B、 , C、 , D、 , -
18、国家非遗“道州龙船赛”每年都吸引着数十万人现场观看比赛,据不完全统计,2023年现场观看龙船比赛人数约万人,预计2025年现场观看龙船比赛的人数约万人,则这两年现场观看龙船比赛人数的年平均增长率约为( )A、 B、 C、 D、
-
19、关于反比例函数 , 下列说法中错误的是( )A、时,y随x的增大而减小 B、当时, C、它的图象与坐标轴无交点 D、当时,y有最小值
-
20、在用公式法解一元二次方程时,代入a,b,c得到 , 则求解的一元二次方程是( )A、 B、 C、 D、