-
1、 如图,点在直线外.
①在直线上任取一点 , 连接;
②以点为圆心,长为半径画弧,交直线于点;
③分别以点和点为圆心,以大于的长为半径画弧,两弧在内交于点 , 作射线;
④以点为圆心,长为半径画弧,交射线于点;
⑤连接 .
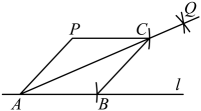 (1)、由②得与的数量关系是;由③得到的结论是 .(2)、求证:四边形是菱形.
(1)、由②得与的数量关系是;由③得到的结论是 .(2)、求证:四边形是菱形. -
2、 化简求值: , 其中 .
-
3、 计算: .
-
4、 如图,在单位长度均为的平面直角坐标系中,放置一个圆柱形笔筒的展开图.其中,侧面展开图的边在坐标轴上,点坐标为 . 将一根长度为的铅笔放入笔筒内,露出笔筒部分的最小长度是(结果保留整数,取3,壁厚忽略不计).
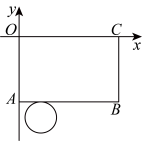
-
5、 编程机器人表演中,一机器人从沙盘平面内某点出发向前直行步后右转 , 沿转后方向直行步后右转 , 再沿转后方向直行步后右转…,依此方式继续行走,第一次回到出发点时,该机器人共走了步.
-
6、 一个数学游戏规则是:如图,在以同一点为位似中心的三个位似三角形的顶点处任意填入9个不同的数,使每个三角形的三个顶点与同一直线上的三个顶点的三个数之和均相等,则 .
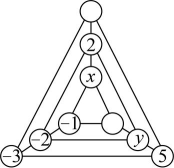
-
7、 如图,⊙是的内切圆, , 则 .
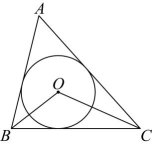
-
8、 不等式组的解集是 .
-
9、 为提升学生艺术素养,学校在周三同时开展了多种文艺社团活动.现从参加器乐、舞蹈和声乐这三个文艺社团的学生中随机抽取两名,他们恰好参加同一社团的概率为 .
-
10、 如图,直线与直线交于点 , 则关于的方程组的解是 .
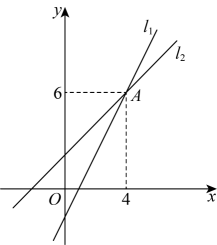
-
11、 老师带领数学小组仅用测角仪和皮尺测量某桥外侧拱顶离水面的高度.如图,拱顶离水面的高度为 , 点 , 是水平地面上两点,且与点 , 均在同一竖直平面内.已知水平地面离水面的高度为2米,测角仪支架高度为1.5米,为达成目的,还需测量的数据是( )
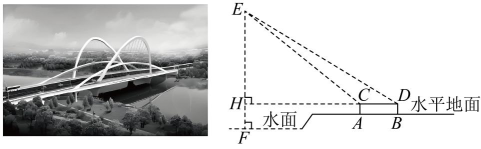 A、的长,的度数 B、的长,的度数 C、的长,的度数 D、的长,的度数
A、的长,的度数 B、的长,的度数 C、的长,的度数 D、的长,的度数 -
12、 函数和的部分图象如图所示,点在的图象上,过点作轴交轴于点 , 交的图象于点 . 若 , 则的值为( )
 A、 B、 C、 D、3
A、 B、 C、 D、3 -
13、 下列判断正确的是( )A、若点关于轴的对称点在第二象限,则 B、夜晚,小明走向一盏路灯,他在地面上的影长由短变长 C、4的平方根是2 D、过一点有且只有一条直线与已知直线垂直
-
14、 《九章算术》中有一段文字的大意是:有人合伙买羊,若每人出5钱,还差45钱;若每人出7钱,还差3钱.问合伙人数、羊价各是多少?设合伙人数为人,羊价为钱,则可列方程组为( )A、 B、 C、 D、
-
15、 如图,将书本上面的橡皮擦沿箭头方向(垂直于右边缘)平移到书本右边缘.在此过程中,下列叙述正确的是( )
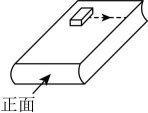 A、主视图不变 B、左视图不变 C、俯视图不变 D、三种视图都不变
A、主视图不变 B、左视图不变 C、俯视图不变 D、三种视图都不变 -
16、 下列运算正确的是( )A、 B、 C、 D、
-
17、 如图,直线被直线所截,根据“同位角相等,两直线平行”判定 , 需要的条件是( )
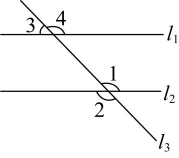 A、 B、 C、 D、
A、 B、 C、 D、 -
18、 如图,数轴上点表示的数可能是( )
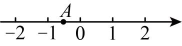 A、 B、 C、 D、1
A、 B、 C、 D、1 -
19、 如图,已知二次函数图象的对称轴为轴,且过坐标原点及点 , 过点作射线平行于轴(点在点上方),点坐标为 , 连接并延长交抛物线于点 , 射线平分 , 过点作的垂线交轴于点 .
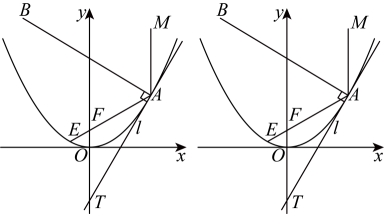 (1)、求二次函数的表达式;(2)、判断直线与二次函数的图象的公共点的个数,并说明理由;(3)、点为轴上的一个动点,且为钝角,请直接写出实数的取值范围.
(1)、求二次函数的表达式;(2)、判断直线与二次函数的图象的公共点的个数,并说明理由;(3)、点为轴上的一个动点,且为钝角,请直接写出实数的取值范围. -
20、 如图,为外接圆的直径,点C为线段上一点(不与D , O重合),点B为的延长线上一点,连接并延长至点M , 满足 .
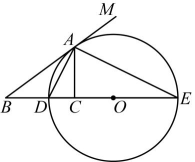 (1)、求证:平分;(2)、证明:;(3)、若射线与相切于点A , , , 求的值.
(1)、求证:平分;(2)、证明:;(3)、若射线与相切于点A , , , 求的值.