相关试卷

1、

(1)、【问题提出】如图①，MN 的长度为定值，在直线l上分别取点 P，Q，使PQ=MN，当AP+PQ+BQ 最小时，找出点 P，Q 的位置；(保留作图痕迹，不写作法)

(2)、【问题解决】某建筑施工队计划修建一个如图②所示的长方形公园，并计划在区域边缘设计一个出入口 EF，且出入口的宽度为20m，AB=80m，AD=40m，P为BC的中点，点P 处为公园的儿童游乐区，点A，B，C，D 均为洗手间，AP，PF，AE为笔直的小路，在修建的过程中要求 AE+PF 的路程最短.请你算出当AE+PF 距离最短时，出入口的左端F到卫生间C的距离.

查看解析
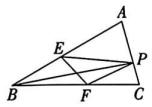
2、如图，P为△ABC边AC上的一点，连接BP，E，F 分别为边AB，BC上的动点，连接PE，PF，EF，若BP=8，∠ABC=30°，求△PEF的周长最小值.

查看解析
3、如图，在△ABC中，∠B=90°，∠ACB=30°，CD平分∠ACB，P，Q 分别是AC，DC上的动点，连接PQ，AQ，若AC=8，求AQ+PQ 的最小值.

查看解析
4、如图，直线l∥m，在直线l，m上分别取点M，N，使MN⊥直线l，连接AM，MN，BN，当AM+MN+BN最小时，求点 M，N的位置.

查看解析
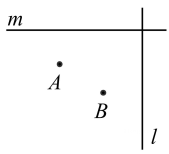
5、如图，A，B是直线m，l外的点，E，P 分别是直线m，l上的动点，当AE+EP+PB 的值最小时，求点E，P的位置.

查看解析
6、如图，B是直线m，l之间一点，E，P 分别是直线m，l上的动点，当BE+BP+EP 的值最小时，求点E，P的位置.

查看解析
7、如图，B是直线m，l之间一点，E，P分别是直线m，l上的动点，当BP+EP 的值最小时，求点 E，点P 的位置.

查看解析
8、如图，已知点 P，Q在直线AB 同侧，在直线AB上求作一点 M，使MP+MQ最短.

查看解析
9、如图，已知点 M，N在直线AB 两侧，在直线AB上求作一点 P，使MP+NP 最短.

查看解析
10、若关于 $x$ 的函数 $y = (m + 2) x^{m^{2} - 2} + x - 3$ 是二次函数，则 $m$ 的值为（）

A、0 B、2 C、 $- 2$ 或2 D、 $- 2$

查看解析
11、某冷冻食品的保存温度是 $（ 15 \pm 2 ） ℃$ ，则该食品的合适的保温范围是.

查看解析
12、a是不为2的有理数，我们把 $\frac{2}{2 - a}$ 称为a的“哈利数”．例如：3的“哈利数”是 $\frac{2}{2 - 3} = - 2$ ， $- 2$ 的“哈利数“是 $\frac{2}{2 - (- 2)} = \frac{1}{2}$ ，已知 $a_{1} = 3$ ， $a_{2}$ 是 $a_{1}$ 的“哈利数”， $a_{3}$ 是 $a_{2}$ 的“哈利数”， $a_{4}$ 是 $a_{3}$ 的“哈利数”，…，依此类推，则 $a_{2024} =$ （）

A、 $- 2$ B、 $\frac{1}{2}$ C、 $\frac{4}{3}$ D、3

查看解析
13、若单项式 $- \frac{1}{2} a^{2 x - 1} b^{4}$ 与 $\frac{3}{2} a^{2} b^{y + 1}$ 的和仍是单项式，则 $|3 x - 2 y| =$ ．

查看解析
14、刘徽在《九章算术注》中有“今两算得失相反，要令正负以名之．”可翻译为“今有两数若其意义相反，则分别叫做正数和负数．”“如果水位上升 $25 cm$ ”记作 $+ 25 cm$ ，那么“水位下降 $18 cm$ ”应表示为（）

A、 $18 cm$ B、 $- 18 cm$ C、 $\pm 18 cm$ D、 $- 7 cm$

查看解析
15、下列说法中，正确的是（）

A、 $- \frac{x^{2} y}{2}$ 的系数是 $- 2$ B、 $3^{2} x y$ 的次数是4 C、 $2 x^{2} - 3 x + 5$ 的一次项系数是3 D、 $- 3 x^{3} y - 2 x^{2} + 5$ 是一个四次三项式

查看解析
16、如图，已知 $△ A B C$ 是等边三角形，D为 $A C$ 上一点， $∠ 1 = ∠ 2$ ， $B D = C E$ ．
．

(1)、求证： $△ A B D ≌ △ A C E$ ；

(2)、求证： $△ A D E$ 是等边三角形．

查看解析
17、如图，已知 $A (1, 2)$ ， $B (4, 1)$ ， $C (3, - 2)$ ．

(1)、画出△ABC此关于y轴对称的图形 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}$ ， $B_{1}$ 的坐标；

(2)、P为x轴上一点，请在图中画出使PA＋PB最小时的点P，并写出点P的坐标．

查看解析
18、定义：如果一个正整数能表示为两个正整数m，n的平方差，且 $m - n > 1$ ，则称这个正整数为“智慧优数”．例如， $16 = 5^{2} - 3^{2}$ ， 16就是一个智慧优数，可以利用 $m^{2} - n^{2} = (m + n) (m - n)$ 进行研究．若将智慧优数从小到大排列，则第2个智慧优数是．

查看解析
19、“香渡栏干屈曲，红妆映、薄绮疏棂．”图1窗棂的外边框为正六边形（如图2），则该正六边形的每个内角为 $°$ ．

查看解析
20、如图，在 $△ A B C$ 中， $A C = 6 cm$ ， $A C$ 的垂直平分线交 $B C$ 于点E，交 $A C$ 于点D，连接 $A E$ ．若 $△ A B E$ 的周长为 $14 cm$ ，则 $△ A B C$ 的周长为 $cm$ ．

查看解析

上一页 682 683 684 685 686 下一页跳转