相关试卷
-
1、计算(1)、(2)、(3)、(4)、
-
2、有理数a,b在数轴上的对应点的位置如图所示,则a,b, , 的大小关系,用“”连接起来 .
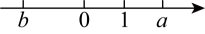
-
3、若 , 则= .
-
4、某天温度最高是 , 最低是 , 这一天温差是 .
-
5、|x﹣2|+|x﹣4|+|x﹣6|+|x﹣8|的最小值是a, , 那么的值为( )A、﹣2 B、﹣1 C、0 D、不确定
-
6、已知 , , , 则的值为( )A、 B、5 C、 D、
-
7、设为最小的正整数,为最大的负整数,是相反数等于本身的数,则的值为( )A、0 B、2 C、0或2 D、
-
8、在数轴上,一个点从原点开始,先向右移动3个单位长度,再向左移动5个单位长度后到达终点,则终点表示的数是( )A、 B、2 C、8 D、
-
9、计算( )A、 B、 C、 D、
-
10、下列各数 , , , , , , , 中,正数有( )A、个 B、个 C、个 D、个
-
11、如果和2025是互为相反数,那么的倒数是( )A、 B、 C、2025 D、
-
12、2025年“五一”期间,乐山大佛“夜游凌云山”项目营收突破300万元,创下同期历史新高.数据3000000用科学记数法表示为( )A、 B、 C、 D、
-
13、为响应“非遗进校园”活动,某校开设了四类非遗文化社团:粤剧,粤绣,英歌舞,醒狮,每位同学只能选择其中一个社团参加.学校随机调查了部分参与社团的学生的情况,根据调查结果绘制了不完整的统计图(如图):
 (1)、本次共调查了名学生,其中参与社团的人数是人;(2)、学校计划从四个社团中任选两个社团进行成果展示,请用列表或画树状图的方法,求同时选中两个社团的概率.
(1)、本次共调查了名学生,其中参与社团的人数是人;(2)、学校计划从四个社团中任选两个社团进行成果展示,请用列表或画树状图的方法,求同时选中两个社团的概率. -
14、有5张看上去无差别的卡片,上面分别写着4,4,5,5,6.(1)、随机抽取一张卡片,则抽取的卡片上的数字是4的概率是 .(2)、从5张卡片中随机抽取2张,请利用列表或画树状图的方法,求所抽取的两张卡片上的数字不同的概率.
-
15、在如图电路中,A灯通电时随机发出红色或紫色光,B灯通电时随机发出红色、绿色或黄色光.
 (1)、电路通电时,B灯发出绿色光的概率是;(2)、电路通电时,请用树状图或列表格求出A、B两灯发出不同颜色光的概率.
(1)、电路通电时,B灯发出绿色光的概率是;(2)、电路通电时,请用树状图或列表格求出A、B两灯发出不同颜色光的概率. -
16、(1)、解方程: .(2)、桌面上有4张卡片,正面分别标有数字2, , 4,4.除数字外完全相同,将卡片背面朝上且打乱摆放顺序,随机抽取2张卡片,求抽取两张卡片的数字都为方程的解的概率.
-
17、如图1是年月的日历,用如图2的“Z”字型覆盖住日历中的五个数,这五个数从小到大依次为 .
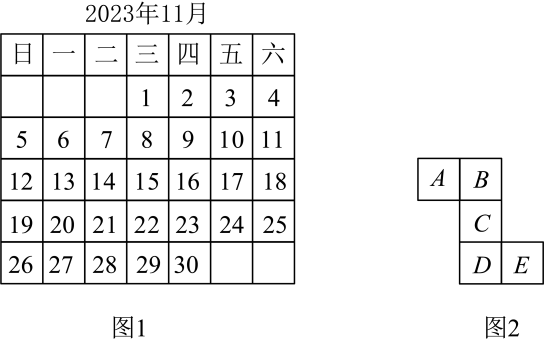 (1)、这五个数的和能被5整除吗?为什么?(2)、若三处的数字之和为 , 请试着求出处的数字.
(1)、这五个数的和能被5整除吗?为什么?(2)、若三处的数字之和为 , 请试着求出处的数字. -
18、 某学校给学生编制的“身份识别条形码”共有12位数字(均为0~9之间的自然数),它是由11位数字代码和最后1位的校验码构成,具体结构如下图:

其中校验码是按照特定的算法计算得来的,用于校验身份识别条形码中前11位数字代码的正确性.具体算法说明如下:
步骤1:计算前11位数字中奇数位数字的和,记为;
步骤2:计算前11位数字中偶数位数字的和,记为;
步骤3:计算 , 记为;
步骤4:取不小于且为10的整数倍的最小数;
步骤5:计算 , 结果即为校验码.
阅读上述材料,回答下列问题:
(1)、某同学的“身份识别条形码”为的 , 则计算过程中的值为 . 校验码的值是 .(2)、如图,某同学的“身份识别条形码”中的一位数字不小心污损了,设这个数字为 , 你能否通过其他信息还原出这位数字 , 进而确定这位同学的班级?如果能,写出你的推理过程,如果不能,说明理由. (3)、如图,一名2024届的同学在知道了校验码的计算方法后,尝试利用自己的身份信息计算校验码,然后惊喜的发现自己的“班级”、“学号”和“校验码”的数字(图中被遮住的数字)是完全一样的,请直接写出这个数字是 .
(3)、如图,一名2024届的同学在知道了校验码的计算方法后,尝试利用自己的身份信息计算校验码,然后惊喜的发现自己的“班级”、“学号”和“校验码”的数字(图中被遮住的数字)是完全一样的,请直接写出这个数字是 .
-
19、观察下面的点阵图和相应的等式,探究其中的规律:
 (1)、在④后面的横线上写出相应的等式:
(1)、在④后面的横线上写出相应的等式:①1=12;②1+3=22;③1+3+5=32;④;⑤1+3+5+7+9=52;…
(2)、请写出第n个等式;(3)、利用(2)中的等式,计算:41+43+45+…+199. -
20、如图是2023年8月份的月历,现用十字框任意框出5个数,如:
 (1)、十字框框出的5个数与十字框中间的数有什么关系?(2)、如果十字框框出的5个数之和为55,那么十字框中间的数是多少?(3)、十字框框出的5个数之和可以是105吗?
(1)、十字框框出的5个数与十字框中间的数有什么关系?(2)、如果十字框框出的5个数之和为55,那么十字框中间的数是多少?(3)、十字框框出的5个数之和可以是105吗?