湘教版数学八年级上册 5.2 勾股定理及逆定理 第一课时 同步分层练习
试卷更新日期:2025-11-19 类型:同步测试
一、夯实基础
-
1. 在下列四组数中,属于勾股数的是( )A、 B、 C、3,5,7 D、5,12,132. 在中, , 、、所对边的长分别为a、b、c,若 , , 那么的值是( )A、2 B、6 C、20 D、363. 如图,在中, , , 点A恰好落在数轴上表示的点上,以原点O为圆心,的长为半径画弧交数轴于点P,使点P落在点A的左侧,则点P所表示的数是( )
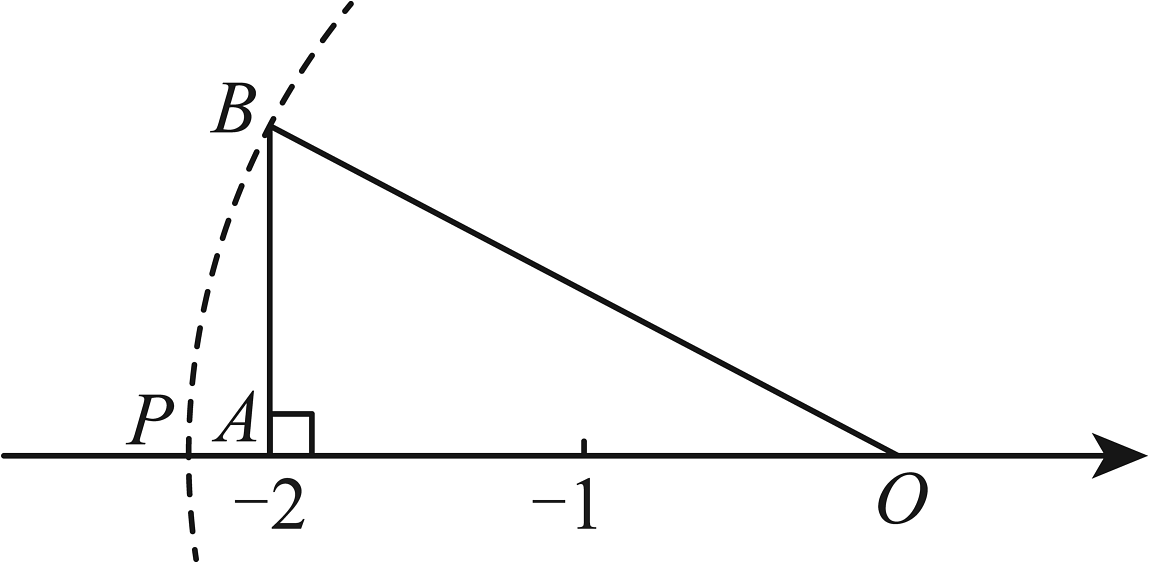 A、 B、 C、 D、4. 如图,在三角形中,已知 , , , 则的大小有可能是( )
A、 B、 C、 D、4. 如图,在三角形中,已知 , , , 则的大小有可能是( ) A、7 B、4 C、6 D、55. 如图,在4×4的正方形网格中,每个小正方形的边长均为1,的顶点都在格点上,则下列结论错误的是( )
A、7 B、4 C、6 D、55. 如图,在4×4的正方形网格中,每个小正方形的边长均为1,的顶点都在格点上,则下列结论错误的是( ) A、 B、 C、 D、6. 直角三角形两条边长分别是6和8,则这个直角三角形的第三边长 .7. 在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.若c=10 cm,a:b=3:4,则△ABC 的周长为8. 如图,在中, , 以和为边向两边分别作正方形,面积分别为和 . 已知 , 且 , 则的值为 .
A、 B、 C、 D、6. 直角三角形两条边长分别是6和8,则这个直角三角形的第三边长 .7. 在△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.若c=10 cm,a:b=3:4,则△ABC 的周长为8. 如图,在中, , 以和为边向两边分别作正方形,面积分别为和 . 已知 , 且 , 则的值为 . 9. 如图,阴影部分的长方形面积是 .
9. 如图,阴影部分的长方形面积是 . 10. 如图,在中,是高 , 则 .
10. 如图,在中,是高 , 则 . 11. 直角三角形的两直角边均扩大到原来的3倍,则斜边扩大到原来的倍.12. 如图,在四边形中, , , , , . 求四边形的面积.
11. 直角三角形的两直角边均扩大到原来的3倍,则斜边扩大到原来的倍.12. 如图,在四边形中, , , , , . 求四边形的面积. 13. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子的长为17米,此人以1米/秒的速度收绳,7秒后船移动到点的位置,问船向岸边移动了多少米?(假设绳子一直保持是直的)
13. 如图,在离水面高度为8米的岸上,有人用绳子拉船靠岸,开始时绳子的长为17米,此人以1米/秒的速度收绳,7秒后船移动到点的位置,问船向岸边移动了多少米?(假设绳子一直保持是直的)
二、能力提升
-
14. 上图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形,设直角三角形的两条直角边长分别为 . 若小正方形面积为7, , 则大正方形的边长为( )
 A、 B、 C、 D、15. 在△ABC中,AB=AC=17,BC=16,则△ABC的面积为( )A、60 B、80 C、100 D、12016. 一个直角三角形,若三边的平方和为200,则斜边长为( )A、8 B、9 C、10 D、1117. 以单位1为边长画一个正方形,以顶点A为圆心、对角线长为半径画弧,与数轴的交点为C(点C在点B左侧),设点C在数轴上表示的数是a,则点A在数轴上表示的数是( )
A、 B、 C、 D、15. 在△ABC中,AB=AC=17,BC=16,则△ABC的面积为( )A、60 B、80 C、100 D、12016. 一个直角三角形,若三边的平方和为200,则斜边长为( )A、8 B、9 C、10 D、1117. 以单位1为边长画一个正方形,以顶点A为圆心、对角线长为半径画弧,与数轴的交点为C(点C在点B左侧),设点C在数轴上表示的数是a,则点A在数轴上表示的数是( ) A、 B、 C、 D、18. 如图()是一把折叠椅实物图,支架与交于点 , . 如图()是椅子打开时的侧面示意图(忽略材料的厚度),椅面与地面水平线平行, , , , 那么折叠后椅子比完全打开时高( ) .
A、 B、 C、 D、18. 如图()是一把折叠椅实物图,支架与交于点 , . 如图()是椅子打开时的侧面示意图(忽略材料的厚度),椅面与地面水平线平行, , , , 那么折叠后椅子比完全打开时高( ) . A、 B、 C、 D、19. 已知P为等边 内一点, 则 .
A、 B、 C、 D、19. 已知P为等边 内一点, 则 . 20. 如图,在中, , AB的垂直平分线交AB于点D,交BC的延长线于点E.若 , , 则EC的长为 .
20. 如图,在中, , AB的垂直平分线交AB于点D,交BC的延长线于点E.若 , , 则EC的长为 . 21. 如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,DE∥BC,CE平分∠DCB,BC=12,AC=16,则DE的长是.
21. 如图,在△ABC中,∠ACB=90°,CD是AB边上的中线,DE∥BC,CE平分∠DCB,BC=12,AC=16,则DE的长是. 22. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是 .
22. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是 . 23. 如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.
23. 如图,长方体的底面边长分别为1cm 和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.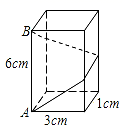 24. 已知:如图,AD、BC相交于点O,AB=CD,AD=CB.
24. 已知:如图,AD、BC相交于点O,AB=CD,AD=CB. (1)、求证:△ABD≌△CDB.(2)、若OB =4,BD=6时,求△OBD中 BD边上的高.
(1)、求证:△ABD≌△CDB.(2)、若OB =4,BD=6时,求△OBD中 BD边上的高.三、拓展创新
-
25.(1)、秋千在平衡位置时,下端A距地面 , 当秋千荡到的位置时,下端距平衡时的水平距离为 , 距地面 , 求秋千的长度.
 (2)、如图,已知一块四边形的草地ABCD , 其中 , , , , , 求这块草地的面积.
(2)、如图,已知一块四边形的草地ABCD , 其中 , , , , , 求这块草地的面积. 26. 如图1,在中, , 直角边在射线上,直角顶点C与射线端点O重合, , , 且满足 .
26. 如图1,在中, , 直角边在射线上,直角顶点C与射线端点O重合, , , 且满足 . (1)、写出a,b的值;(2)、如图2,向右匀速移动 , 在移动的过程中的形状大小不变,且边在射线上匀速向右运动,移动的速度为2个单位/秒,移动的时间为t秒,连接 .
(1)、写出a,b的值;(2)、如图2,向右匀速移动 , 在移动的过程中的形状大小不变,且边在射线上匀速向右运动,移动的速度为2个单位/秒,移动的时间为t秒,连接 .①若为等腰三角形,求t的值;
②在移动的过程中,能否使为直角三角形?若能,求出t的值;若不能,说明理由.