相关试卷

1、已知 $| a | = 3$ ， $b = - 8$ ， $a b < 0$ ，则 $a + b$ 的值为（）

A、 $- 5$ B、5 C、 $- 11$ D、 $\pm 5$

查看解析
2、设 $a$ 为最小的正整数， $b$ 为最大的负整数， $c$ 是相反数等于本身的数，则 $a + c - b$ 的值为（）

A、0 B、2 C、0或2 D、 $- 2$

查看解析
3、在数轴上，一个点从原点开始，先向右移动3个单位长度，再向左移动5个单位长度后到达终点，则终点表示的数是（）

A、 $- 2$ B、2 C、8 D、 $- 8$

查看解析
4、计算 $\overset{m 个}{\overset{︷}{2 + 2 + 2 + ⋯ ⋯ + 2}} + \overset{n 个}{\overset{︷}{3 \times 3 \times 3 \times ⋯ ⋯ \times 3}} =$ （）

A、 $2 m + n^{3}$ B、 $m^{2} + 3^{n}$ C、 $2^{m} + 3 n$ D、 $2 m + 3^{n}$

查看解析
5、下列各数 ${(- 3)}^{2}$ ， $0$ ， $- {(- \frac{1}{2})}^{2}$ ， $\frac{22}{7}$ ， ${(- 1)}^{2025}$ ， $- 2^{2}$ ， $- (- 8)$ ， $- | - \frac{3}{4} |$ 中，正数有（）

A、 $5$ 个 B、 $4$ 个 C、 $3$ 个 D、 $2$ 个

查看解析
6、如果 $a$ 和2025是互为相反数，那么 $a$ 的倒数是（）

A、 $- 2025$ B、 $\frac{1}{2025}$ C、2025 D、 $- \frac{1}{2025}$

查看解析
7、2025年“五一”期间，乐山大佛“夜游凌云山”项目营收突破300万元，创下同期历史新高．数据3000000用科学记数法表示为（）

A、 $3 \times 1 0^{5}$ B、 $3 \times 1 0^{6}$ C、 $3 \times 1 0^{7}$ D、 $3 \times 1 0^{8}$

查看解析
8、为响应“非遗进校园”活动，某校开设了四类非遗文化社团： $A$ 粤剧， $B$ 粤绣， $C$ 英歌舞， $D$ 醒狮，每位同学只能选择其中一个社团参加．学校随机调查了部分参与社团的学生的情况，根据调查结果绘制了不完整的统计图（如图）：

(1)、本次共调查了名学生，其中参与 $B$ 社团的人数是人；

(2)、学校计划从 $A ， B ， C ， D$ 四个社团中任选两个社团进行成果展示，请用列表或画树状图的方法，求同时选中 $A 和 C$ 两个社团的概率．

查看解析
9、有5张看上去无差别的卡片，上面分别写着4，4，5，5，6．

(1)、随机抽取一张卡片，则抽取的卡片上的数字是4的概率是．

(2)、从5张卡片中随机抽取2张，请利用列表或画树状图的方法，求所抽取的两张卡片上的数字不同的概率．

查看解析
10、在如图电路中，A灯通电时随机发出红色或紫色光，B灯通电时随机发出红色、绿色或黄色光．

(1)、电路通电时，B灯发出绿色光的概率是；

(2)、电路通电时，请用树状图或列表格求出A、B两灯发出不同颜色光的概率．

查看解析
11、

(1)、解方程： $x^{2} - 6 x + 8 = 0$ ．

(2)、桌面上有4张卡片，正面分别标有数字2， $- 2$ ， 4，4．除数字外完全相同，将卡片背面朝上且打乱摆放顺序，随机抽取2张卡片，求抽取两张卡片的数字都为方程 $x^{2} - 6 x + 8 = 0$ 的解的概率．

查看解析
12、如图1是 $2023$ 年 $11$ 月的日历，用如图2的“Z”字型覆盖住日历中的五个数，这五个数从小到大依次为 $A 、 B 、 C 、 D 、 E$ ．

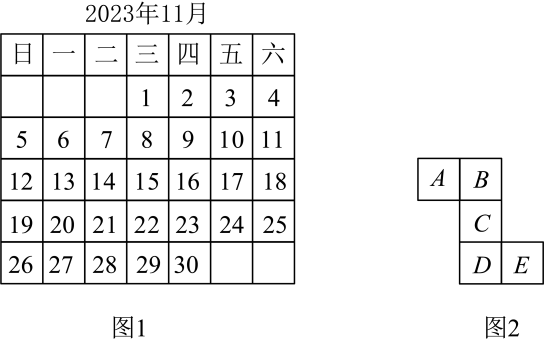(1)、这五个数的和能被5整除吗？为什么？

(2)、若 $B 、 C 、 D$ 三处的数字之和为 $42$ ，请试着求出 $A$ 处的数字．

查看解析
13、某学校给学生编制的“身份识别条形码”共有12位数字（均为0～9之间的自然数），它是由11位数字代码和最后1位的校验码构成，具体结构如下图：
其中校验码是按照特定的算法计算得来的，用于校验身份识别条形码中前11位数字代码的正确性．具体算法说明如下：
步骤1：计算前11位数字中奇数位数字的和，记为 $m$ ；
步骤2：计算前11位数字中偶数位数字的和，记为 $n$ ；
步骤3：计算 $3 m + n$ ，记为 $p$ ；
步骤4：取不小于 $p$ 且为10的整数倍的最小数 $q$ ；
步骤5：计算 $q - p$ ，结果即为校验码．
阅读上述材料，回答下列问题：

(1)、某同学的“身份识别条形码”为的 $04220220133 □$ ，则计算过程中 $p$ 的值为．校验码 $□$ 的值是．

(2)、如图，某同学的“身份识别条形码”中的一位数字不小心污损了，设这个数字为 $x$ ，你能否通过其他信息还原出这位数字 $x$ ，进而确定这位同学的班级？如果能，写出你的推理过程，如果不能，说明理由．

(3)、如图，一名2024届的同学在知道了校验码的计算方法后，尝试利用自己的身份信息计算校验码，然后惊喜的发现自己的“班级”、“学号”和“校验码”的数字（图中被遮住的数字）是完全一样的，请直接写出这个数字是．

查看解析
14、观察下面的点阵图和相应的等式，探究其中的规律：

(1)、在④后面的横线上写出相应的等式：
①1＝1²；②1＋3＝2²；③1＋3＋5＝3²；④；⑤1＋3＋5＋7＋9＝5²；…

(2)、请写出第n个等式；

(3)、利用（2）中的等式，计算：41＋43＋45＋…＋199．

查看解析
15、如图是2023年8月份的月历，现用十字框任意框出5个数，如：

(1)、十字框框出的5个数与十字框中间的数有什么关系？

(2)、如果十字框框出的5个数之和为55，那么十字框中间的数是多少？

(3)、十字框框出的5个数之和可以是105吗？

查看解析
16、十九世纪中叶，诞生了一个新的几何学分支“拓扑学（又称‘位置解析’）”．它所研究的是几何图形这样一些最基本的、最深刻的性质：图形经受剧烈的变形，以致所有度量性质和射影性质都失去之后，这些性质仍然存在．数学家们找到若干个令人叹为观止的实例，例如著名的Mobius带、Klein瓶……
请看如图，你能否将正方形图中上方的小方块与下方的对应的小方块用平面内不相交的实线连起来，且要求连线只能在该正方形内部的空白处．

查看解析

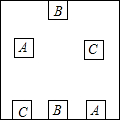
17、火柴拼图是一种道具简单、开启思维、挖掘智力、陶冶情趣的数字游戏．这种游戏形式万千，可简可繁．七年级的同学们学了“用字母表示数”和“列代数式”的内容后，数学课外活动小组的同学们利用课外活动时间举行用火柴棒拼图的实践活动．他们按照下图所示的方法拼图，探究不同图形中共拼出的三角形个数，正方形的个数及所用火柴棒的根数与所拼图之间的关系，请你参与进去进行数学探究活动．

(1)、观察：观察下图中正方形的个数及所用火柴棒根数，并填写下表中的空格：

	第1个	第2个	第3个	第4个	…
拼成三角形个数	1	2			…
拼成的正方形个数	3	5			…
所用火柴棒总根数	12	20			…

(2)、探究：按如图所示的方法拼成的第n个图中，三角形和正方形的个数各有多少？所用的火柴棒总根数是多少？（用含n的代数式表示，并与同学们进行交流）

查看解析

18、如图的数字三角形有一定的规律，请按规律填上空缺的数．

查看解析
19、12人乘车去某地，可供租的车辆有两种：一种车可乘8人，另一种车可乘4人．

(1)、请给出3种以上的租车方案；

(2)、如果第一种车的租金是300元/天，第二种车的租金是200元/天，那么采用哪种方案费用最少？

查看解析
20、由8根火柴棒搭成1个正方形（如图），你能移动火柴棒（不减少火柴棒总数），使得新图形的面积为这个正方形面积的一半吗？

查看解析

上一页 628 629 630 631 632 下一页跳转