-
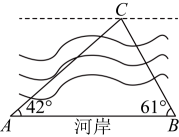
1、小明和小军两位同学对某河流的宽度进行测量,如图所示,两人分别站在同侧河岸上的点、处,选取河对岸的一块石头作为测量点(点在同一水平面内),小明同学在点处测得为 , 小军同学在点处测得为 , 两人之间的距离为60米,求此河流的宽度.(参考数据:)
-
2、某校建议学生利用周末时间积极参加社会实践活动.某一周末有两个项目供学生选择:A文明交通劝导志愿行,B乡村教育关爱行,每名学生只能选择其中一个项目.(1)、甲同学选择A项目的概率为;(2)、请用画树状图的方法,求甲、乙、丙三位同学恰好选择同一项目的概率.
-
3、2025年2月,江苏省教育厅印发《关于在义务教育学校实施“2・15专项行动”的通知》,明确提出“中小学生每天综合体育活动时间不低于2小时”.某校采取多种举措,确保学生每天有充足的体育活动时间,同时监测学生的体质健康情况.为此,学校从全体男生中随机抽取部分学生调查他们的立定跳远成绩,并把成绩分成五档(A档、B档、C档、D档、E档 , 单位:),绘制成统计图.其中部分数据丢失,请结合统计图,完成下列问题:
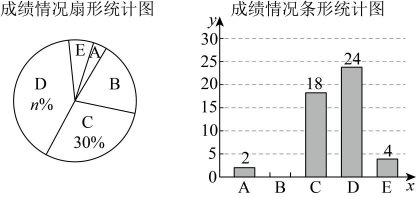 (1)、扇形统计图中的值为 , 条形统计图中“B档”成绩的人数为;(2)、本次抽测中,立定跳远成绩的中位数落在档;(3)、若该校共有1200名男生,请你估计该校立定跳远成绩为“E档”的男生人数.
(1)、扇形统计图中的值为 , 条形统计图中“B档”成绩的人数为;(2)、本次抽测中,立定跳远成绩的中位数落在档;(3)、若该校共有1200名男生,请你估计该校立定跳远成绩为“E档”的男生人数. -
4、先化简,再求值: , 其中 .
-
5、计算: .
-
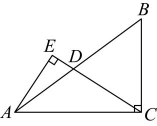
6、如图,在中, , 点在边上(不与A,B重合),过点作 , 垂足为点 , 则的最小值是 .
-
7、方程的两个根分别是 , 则
-
8、一块梯形木板 , 按如图方式设计一个矩形桌面(点在边上).当时,矩形桌面面积最大.

-
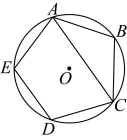
9、如图,正五边形内接于 , 连接 , 则的度数为 .
-
10、已知圆锥的底面半径为3,高为4,则其侧面积为 .
-
11、等腰三角形的两边长分别为和 , 则该等腰三角形的周长为 .
-
12、某公司在一次招聘中,分笔试和面试两部分,笔试和面试成绩按计算最终成绩.小李的笔试成绩为85分,面试成绩为90分,则小李的最终成绩为分.
-
13、点在第一象限,则实数的取值范围是 .
-
14、要使分式有意义,实数的取值范围是 .
-
15、如图,点、在双曲线上,直线分别与轴、轴交于点、 , 与双曲线交于点 , 连接 , 若 , , 则的值为( )
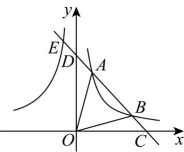 A、 B、 C、 D、
A、 B、 C、 D、 -
16、《九章算术》中记载:“今有牛五、羊二,值金十两;牛二、羊五,值金八两.问牛羊各值金几何?”译文:“今有牛5头,羊2头,共值金10两;牛2头,羊5头,共值金8两.问牛羊每头各值金多少?”若设牛每头值金两,羊每头值金两,则可列方程组是( )A、 B、 C、 D、
-
17、在平面直角坐标系中,点的坐标为 , 将线段绕着点逆时针旋转得线段 , 则点的坐标为( )
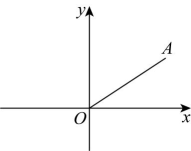 A、 B、 C、 D、
A、 B、 C、 D、 -
18、如图,在中, , 点、、分别是边、、的中点,则下列结论错误的是( )
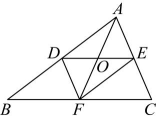 A、 B、 C、 D、
A、 B、 C、 D、 -
19、某几何体的三视图如图所示,这个几何体是( )
 A、圆柱 B、圆锥 C、正方体 D、长方体
A、圆柱 B、圆锥 C、正方体 D、长方体 -
20、宿迁市年第一季度总量突破一千亿大关,约为亿元.数据亿用科学记数法表示为( )A、 B、 C、 D、