-
1、我们约定:不等式组m<x<n , m<x≤n , m≤x<n , m≤x≤n的“长度”均为d=n-m , (m<n),不等式组的整数解称为不等式组的“整点”.例如:-2<x≤2的“长度”d=2-(-2)=4,“整点”为x=-1,0,1,2.根据该约定,解答下列问题:(1)、不等式组的“长度”d= ;“整点”为;(2)、若不等式组的“长度”d=2,求a的取值范围;(3)、若不等式组的“长度 , 此时是否存在实数m使得关于y的不等式组恰有4个“整点”,若存在,求出m的取值范围;若不存在,请说明理由.
-
2、已知在平面直角坐标系中,点A的坐标是(0,2),点P是第一象限内一动点.
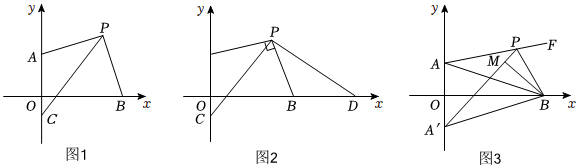 (1)、如图1,若动点P(a , b)满足|3a-9|+(3-b)2=0,求点P的坐标;(2)、如图2,在第(1)问的条件下,且PA⊥PB ,
(1)、如图1,若动点P(a , b)满足|3a-9|+(3-b)2=0,求点P的坐标;(2)、如图2,在第(1)问的条件下,且PA⊥PB ,①求点B的坐标;
②当∠APB=∠CPD , 求OD-OC的值.
(3)、如图3,若OA=OA' , 且BM⊥PA' , 若动点P满足∠APA'=2∠OBA' , 问:的值是否发生变化?若变化,请说明理由,若不变化,请求出其值. -
3、
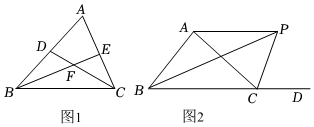 (1)、如图1,在△ABC中,∠B、∠C的平分线BE , CD相交于点F , ∠ABC=40°,∠A=60°,求∠BFC的度数;(2)、如图2,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P , 若∠BPC=42°,
(1)、如图1,在△ABC中,∠B、∠C的平分线BE , CD相交于点F , ∠ABC=40°,∠A=60°,求∠BFC的度数;(2)、如图2,△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P , 若∠BPC=42°,①求∠CAB的度数;
②求∠CAP的度数.
-
4、我国国产动画电影“哪吒2魔童闹海”票房突破了150亿,商家推出A、B两种类型的哪吒纪念娃娃,若用380元可购进A种娃娃7件,B种娃娃8件;用340元可购进A种娃娃11件,B种娃娃4件.(1)、求A、B两种娃娃的进价分别为多少?(2)、若每件A种娃娃售价为25元,每件B种娃娃售价为37元,某商店准备用不超过900元购进A、B两种娃娃40件,且这两种娃娃全部售出后总获利不低于216元,问共有几种方案并求出利润最大值?
-
5、请将下列证明过程补充完整:如图,已知CD⊥AB , GF⊥AB , ∠1=∠2,求证:∠FEC+∠ECB=180°.

证明:∵CD⊥AB , GF⊥AB ;
∴∠CDF=∠GFB=90° ;
∴CD∥ (同位角相等,两直线平行);
∴∠FGB=∠2 ;
∵∠1=∠2(已知);
∴∠1= ;
∴EF∥BC ;
∴∠FEC+∠ECB=180° ;
-
6、如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3)将△ABC平移得到△A1B1C1 , 其中A的对应点是A1(2,1);
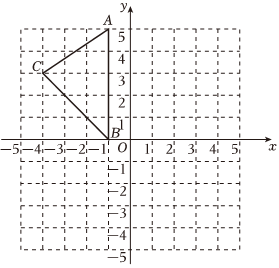 (1)、写出点B , C的对应点B1 , C1的坐标:B1 , C1;(2)、在图中画出△A1B1C1;(3)、设点P在x轴上,且△BCP的面积等于△ABC的面积,求出点P的坐标.
(1)、写出点B , C的对应点B1 , C1的坐标:B1 , C1;(2)、在图中画出△A1B1C1;(3)、设点P在x轴上,且△BCP的面积等于△ABC的面积,求出点P的坐标. -
7、求下列各式中x的值:(1)、;(2)、(x-2)2=169.
-
8、计算:.
-
9、已知关于x的不等式组的解集是-1<x<1,则(a+1)(b-1)= .
-
10、若关于x , y的方程组的解x与y互为相反数,则k的值为.
-
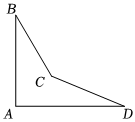
11、一个零件的形状如图,按规定∠A=90°,∠B=∠D=25°,判断这个零件是否合格,只要检验∠BCD的度数就可以了.量得∠BCD=140°,这个零件(填“合格”或“不合格”).
-
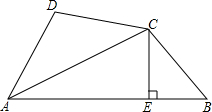
12、已知AC平分∠DAB , CE⊥AB于E , AB=AD+2BE , 则下列结论:①AE=(AB+AD);②∠DAB+∠DCB=180°;③CD=CB;④S△ACE-S△BCE=S△ADC . 其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个 -
13、俄罗斯方块是一款经典休闲益智游戏,如图是小宇玩俄罗斯方块时某一时刻的截图,若在以O为原点建立的平面直角坐标系中,小宇将上方的方块先向左移动2个格子,再向下移动6个格子后,点A恰好落在点B(3,1)处,则上方的方块移动前点A所在位置的坐标为( )
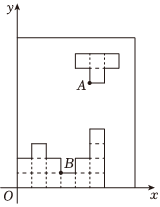 A、(4,7) B、(5,6) C、(5,7) D、(7,5)
A、(4,7) B、(5,6) C、(5,7) D、(7,5) -
14、如图,DE⊥AC , BF⊥AC , 垂足分别是E , F , 且DE=BF , 若利用“HL”证明△DEC=△BFA , 则需添加的条件是( )
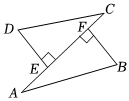 A、EC=FA B、DC=BA C、∠D=∠B D、∠DCE=∠BAF
A、EC=FA B、DC=BA C、∠D=∠B D、∠DCE=∠BAF -
15、有4根长度分别为2、4、6、7的木条,从中任意选出三根,其中能构成三角形的有( )A、1种 B、2种 C、3种 D、4种
-
16、每年3月21日是世界睡眠日,良好的睡眠状况是保持身体健康的重要基础,为了解某校800名初三学生的睡眠时间,从17个班级中抽取100名学生进行调查,下列说法正确的是( )A、800名学生是总体 B、100是样本容量 C、17个班级是抽取的一个样本 D、每名学生是个体
-
17、下列等式正确的是( )A、=-3 B、=±12 C、=-2 D、-=-5
-
18、若a<b , 则下列不等式一定成立的是( )A、a+b<2b B、a-c<b+c C、ac<bc D、
-
19、把无理数表示在数轴上,在这四个无理数中,被墨迹(如图所示)覆盖住的无理数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、小明在参观科技馆时,发现很多矿物的结晶体有着其独特的几何形态和内在规律.
【发现问题】
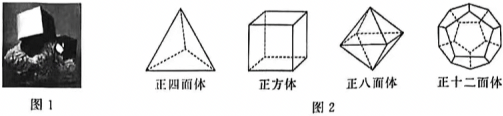
黄铁矿的晶体(如图1)是一个正方体:它由六个面组成,每个面都是全等的正方形,每个顶点都连接3条棱.小明查阅资料后了解到,这种各面都是全等的正n边形,且各顶点连接r(r≥3)条棱的立体图形称为正多面体,如正方体又称为正六面体.
【提出问题】
小明思考:这样的正多面体有几个?
【分析问题】
一个正F面体的每个面都是全等的正n边形,有V个顶点,E条棱,且每个顶点都连接r条棱.小明对部分正F面体(如图2)进行了观察,列出以下数据.
正多面体
F
n
V
E
r
正四面体
4
3
4
6
3
正方体
6
4
8
12
3
正八面体
8
3
6
12
4
(1)、根据表中的数据,请写出F,V,E之间存在的等量关系式: .(2)、小明进一步发现,正F面体中棱数与各面的边数之和以及棱数与各面的顶点数之和存在着一定的关系.①从而出发:
以正方体为例,它有6个面,每个面都有4条边,则六个面的边数之和为24.又因为正方体的两个面共用一条边,所以正方体的棱数为12.
正F面体的棱数E= ;(用含n,F的代数式表示)
②从顶点出发:正F面体的棱数E= .(用含r,V的代数式表示)
(3)、【解决问题】已知一个正多面体有30条棱,且每个顶点连接3条棱,求这个正多面体的面数.
(4)、满足正多面体定义的几何体一共有几个?请说明你的理由.