人教版七（上）第二章有理数的运算单元测试基础卷

试卷更新日期：2025-10-05 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，“一带一路”涉及沿线 $65$ 个国家，总涉及人口约 $4500000000$ ，将数据 $4500000000$ 用科学记数法表示为（）

A、 $0.45 \times 10^{10}$ B、 $4.5 \times 10^{9}$ C、 $45 \times 10^{8}$ D、 $4.5 \times 10^{7}$

查看试题解析
2. 计算 $3 - (- 3)$ 的结果等于（）

A、 $- 6$ B、0 C、3 D、6

查看试题解析
3. 把2.9815精确到十分位的近似数是（）．

A、2.9 B、3 C、2.98 D、3.0

查看试题解析
4. 计算 $\underset{m 个 3}{\underset{⏟}{3 + 3 + 3 + \dots + 3}} + \underset{n 个 4}{\underset{⏟}{4 \times 4 \times 4 \times \dots \times 4}}$ 的结果是（　　）

A、3 $m + 4^{n}$ B、 $m^{3} + 4 n$ C、 $3^{m} + 4 n$ D、3 $m + n^{4}$

查看试题解析
5. 在简便运算时，把 $24 \times (- 99 \frac{47}{48})$ 变形成最合适的形式是（）

A、 $24 \times (- 100 + \frac{1}{48})$ B、 $24 \times (- 100 - \frac{1}{48})$ C、 $24 \times (- 99 - \frac{47}{48})$ D、 $24 \times (- 99 + \frac{47}{48})$

查看试题解析
6. 小华作业本中有四道计算题： $0 - (- 5) = - 5$ ； $(- 3) + (- 9) = - 12$ ； $\frac{2}{3} \times (- \frac{9}{4}) = - \frac{3}{2}$ ； $(- 36) \div (- 9) = - 4$ ．其中他做对的题的个数是（　　）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
7. 某电影院1号厅正在放映电影《哪吒之魔童闹海》，甲、乙两名工作人员根据1号厅的观影人数，说法如下：
甲：“观影人数不超过90人．”
乙：“观影人数不足100人．”
已知甲的说法错误，乙的说法正确，则在1号厅的观影人数可能为（　　）

A、90 B、96 C、100 D、101

查看试题解析
8. 下面结论正确的有（　　）
①两个有理数相加，和一定大于每一个加数．
②一个正数与一个负数相加得正数．
③两个负数和的绝对值一定等于它们绝对值的和．
④两个正数相加，和为正数．
⑤两个负数相加，绝对值相减．
⑥正数加负数，其和一定等于0．

A、0个 B、1个 C、2个 D、3个

查看试题解析
9. 现定义一种新运算“*”，规定 $a * b = a b + a - b$ ，如 $1 * 3 = 1 \times 3 + 1 - 3$ ，则 $(- 2 * 5) * 6$ 等于（）

A、 $- 125$ B、125 C、 $- 120$ D、120

查看试题解析
10. 小宸的综合实践活动报告部分信息如下图，则用十六进制表示 $D \times E$ 的结果是（　　）
综合实践活动：寻找数和计算工具的发展足迹
十六进制：缝十六进一，采用数字 $0 - 9$ 和字母 $A - F$ 共16个计数符号．
十六进制的符号和十进制的数的对应关系：
16进制
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
10进制
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
例： $2 + A = C$ ， $5 + E = 13 ， D + F = 1 C$

A、182 B、DE C、 $B 2$ D、 $B 6$

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 有理数 $12356900$ 精确到万位是（结果用科学记数法表示）．

查看试题解析
12. 计算： $(- 2) \div \frac{2}{3} \times (- 3) =$ ．

查看试题解析
13. 下表是10筐蔬菜的质量记录，每以20kg为标准质量（高于标准质量记为“+”），则这10筐蔬菜总质量为kg
筐数
2
3
1
2
2
与标准质量比较/kg
-0.8
+0.5
-0.5
+0.4
+0.5

查看试题解析
14. 定义一种新运算： $a * b = a^{2} - 3 b$ ，则 $3 * (- 1) =$ ．

查看试题解析
15. 若 $| x - 2 | + {(y + 3)}^{2} = 0$ ，则 $y^{x}$ ＝

查看试题解析

三、解答题：本大题共8小题，共75分.

16. 计算：

(1)、 $(- 7) \times 5 - (- 36) \div 4$ ；

(2)、 $- 1^{4} - 16 \div {(- 2)}^{3} + |- \frac{3}{2}| \times {(- 1)}^{2023}$ ．

查看试题解析
17. 问题：10袋小麦称后记录（单位： $kg$ ）如图所示，10袋小麦平均每袋多少千克？
经过分析，某小组同学们的思路是：以 $50 kg$ 为标准，超过的记为正数，不足的记为负数，求出这10个数的平均数后再加50．

查看试题解析
18. 小明早晨跑步，他从自己家出发，向东跑了 $2 km$ 到达小彬家，继续向东跑了 $1.5 km$ 到达小红家，然后又向西跑了 $4.5 km$ 到达学校，最后又向东跑回到自己家．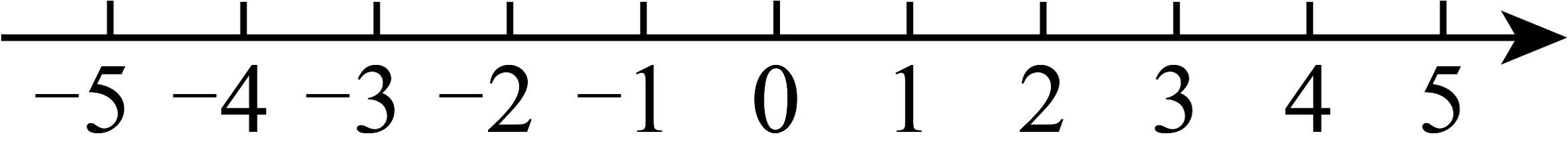

(1)、以小明家为原点，向东为正方向，用1个单位长度表示 $1 km$ ，在图中的数轴上，分别用点A表示出小彬家，用点 $B$ 表示出小红家，用点 $C$ 表示出学校的位置；

(2)、求小彬家与学校之间的距离；

(3)、如果小明跑步的速度是 $250 m / min$ ，那么小明跑步一共用了多长时间？

查看试题解析
19. 外卖送餐为我们生活带来了许多便利，某学习小组调查了一名外卖小哥一周的送餐情况，规定送餐量超过50单（送一次外卖称为一单）的部分记为“ $+$ ”，低于50单的部分记为“ $-$ ”，下表是该外卖小哥一周的送餐量：
星期
一
二
三
四
五
六
七
送餐量（单位：单）
$- 3$
$+ 4$
$- 5$
$+ 14$
$- 8$
$+ 7$
$+ 12$

(1)、在这一周中，该外卖小哥送餐量最多的一天比最少的一天多多少单？

(2)、该外卖小哥这一周平均每天送餐量是多少单？

查看试题解析
20. 小明同学在学习完有理数的运算后，对运算产生了浓厚的兴趣，她借助有理数的运算，定义了一种新运算“ $\oplus$ ”，运算规则为： $a \oplus b = a \times b + 2$ ．如： $2 \oplus 6 = 2 \times 6 + 2$

(1)、求 $2 \oplus 4$ 的值；

(2)、求 $(- 3) \oplus (2 \oplus \frac{1}{2})$ 的值．

查看试题解析
21. 数形结合是运算过程中的重要思想方法，小明将一根木棒放在如图1所示的数轴（单位长度为 $1 cm$ ）上，木棒左端与数轴上的点A重合，右端与数轴上的点B重合．

(1)、若数轴上A点表示的数为 $- 1$ ， B点表示的数为2，若将点A移动到点B，则点A移动的距离为______．

(2)、若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为30；若将木棒沿数轴向左水平移动，则当它的右端移动到点A时，它的左端在数轴上所对应的数为3，由此可得这根木棒的长为______；图中点A所表示的数是______；点B所表示的数是______．

(3)、知识迁移：爸爸对小明说：“我若是你现在这么大，你还要14年才出生；你若是我现在这么大，我就67岁啦！”请求出爸爸的年龄．

查看试题解析
22. 出租车司机老姚某天上午营运全是在南北走向的兴海路上进行，如果规定向南为正，向北为负，他这天上午行车里程（单位： $km$ ）如下：
$+ 8, - 5, - 4, + 6, - 3, - 2, - 10, + 6$ ．

(1)、将第几名乘客送到目的地时，老姚刚好回到上午出发点？

(2)、将最后一名乘客送到目的地时，老姚距上午出发点多远？在出发点的南面还是北面？

(3)、若汽车耗油量为 $0.075 L/km$ ，这天上午老姚的出租车耗油多少L？

查看试题解析
23. 阅读材料：
我们平常用的是十进制，如 $1967 = 1 \times 10^{3} + 9 \times 10^{2} + 6 \times 10 + 7 ，$ 表示十进制的数要用10个数码：0，1，2，3，4，5，6，7，8，9.在计算机中用的是二进制，只有两个数码：0，1，如二进制中的 $111 = 1 \times 2^{2} + 1 \times 2 + 1 ，$ ，相当于十进制中的7， $11011 = 1 \times 2^{4} + 1 \times 2^{3} + 0 \times 2^{2} + 1 \times 2 +$ 1，相当于十进制中的27.
请你计算：

(1)、二进制中的1011相当于十进制中的哪个数?

(2)、二进制中的哪个数相当于十进制中的8?

查看试题解析

星期	一	二	三	四	五	六	七
送餐量（单位：单）	$- 3$	$+ 4$	$- 5$	$+ 14$	$- 8$	$+ 7$	$+ 12$

16进制	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
10进制	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15

筐数	2	3	1	2	2
与标准质量比较/kg	-0.8	+0.5	-0.5	+0.4	+0.5

人教版七（上） 第二章 有理数的运算 单元测试基础卷

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

二、填空题：本大题共5小题，每小题3分，共15分.

三、解答题：本大题共8小题，共75分.

人教版七（上）第二章有理数的运算单元测试基础卷