第五章《直角三角形》基础卷—湘教版数学八(上)单元分层测
试卷更新日期:2025-10-05 类型:单元试卷
一、选择题:本题共10小题,每小题3分,共30分
-
1. 下列各组数中,不是勾股数的是( )A、5,8,12 B、30,40,50 C、9,40,41 D、6,8,102. 具备下列条件的△ABC中,不是直角三角形的是( )A、∠A+∠B=∠C B、∠A-∠B=∠C C、∠A:∠B:∠C=1:2:3 D、∠A=∠B=3∠C3. 如图,在等边中, , , , 交于点 , 则的度数是( )
 A、 B、 C、 D、4. 如图,一场暴雨过后,垂直于地面的一棵树在距离地面2m 处折断,树尖B 恰好碰到地面,经测量∠ABC=30°,则树原来的高度为 ( )
A、 B、 C、 D、4. 如图,一场暴雨过后,垂直于地面的一棵树在距离地面2m 处折断,树尖B 恰好碰到地面,经测量∠ABC=30°,则树原来的高度为 ( )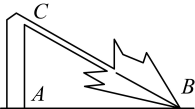 A、6m B、9m C、10m D、12m5. 如图,在中,在数轴上,以点为圆心,的长为半径画弧,交数轴于点 , 则点表示的数是( )
A、6m B、9m C、10m D、12m5. 如图,在中,在数轴上,以点为圆心,的长为半径画弧,交数轴于点 , 则点表示的数是( ) A、 B、 C、 D、6. 在中, , 、、所对边的长分别为a、b、c,若 , , 那么的值是( )A、2 B、6 C、20 D、367. 如图,已知 , 若用 “”判定和全等,则需要添加的条件是( )
A、 B、 C、 D、6. 在中, , 、、所对边的长分别为a、b、c,若 , , 那么的值是( )A、2 B、6 C、20 D、367. 如图,已知 , 若用 “”判定和全等,则需要添加的条件是( ) A、 B、 C、 D、8. 如图,在中, , 依据尺规作图痕迹,给出结论:①;结论② . 下列判断正确的是( )
A、 B、 C、 D、8. 如图,在中, , 依据尺规作图痕迹,给出结论:①;结论② . 下列判断正确的是( ) A、①②都正确 B、①正确,②错误 C、①错误,②正确 D、①②都错误9. 如图,在中, , , , BD平分 , 则点D到AB的距离等于( )
A、①②都正确 B、①正确,②错误 C、①错误,②正确 D、①②都错误9. 如图,在中, , , , BD平分 , 则点D到AB的距离等于( ) A、4 B、3 C、2 D、110. 如图,在的正方形网格中,A,B,C,D是格点,则下列线段长度最长是( )
A、4 B、3 C、2 D、110. 如图,在的正方形网格中,A,B,C,D是格点,则下列线段长度最长是( ) A、AB B、AD C、AC D、AE
A、AB B、AD C、AC D、AE二、填空题:本题共8小题,每小题3分,共24分
-
11. 在Rt△ABC中,斜边上的中线CD=8,则斜边AB的长是12. 如图,在中, , 是高, , 若 , 则 .
 13. 如图,在5×5的正方形网格中, 的顶点均在格点上,若 , 则点 P 与点重合.(填“D”“E”或“F”,且点D,E,F均为格点)
13. 如图,在5×5的正方形网格中, 的顶点均在格点上,若 , 则点 P 与点重合.(填“D”“E”或“F”,且点D,E,F均为格点) 14. 如图,在和中, , , , 则点 , 之间的距离为 .
14. 如图,在和中, , , , 则点 , 之间的距离为 . 15. 如图,中,平分 , 平分 , 过点O作交于点M交于点N,若周长为15,周长为24,则 .
15. 如图,中,平分 , 平分 , 过点O作交于点M交于点N,若周长为15,周长为24,则 . 16. 如图,在△ABC中,∠A=90°,AB=6,BC=10,BC的垂直平分线分别交AC,BC于点D,E,则AD的长为.
16. 如图,在△ABC中,∠A=90°,AB=6,BC=10,BC的垂直平分线分别交AC,BC于点D,E,则AD的长为. 17. 如图,将长方形纸片沿其对角线折叠,使点落在点的位置,与交于点 . 若 , 求图中阴影部分的周长 .
17. 如图,将长方形纸片沿其对角线折叠,使点落在点的位置,与交于点 . 若 , 求图中阴影部分的周长 .
三、解答题:本题共8小题,共66分
-
18. 如图,A,B,P是方格纸中的格点.请按要求画以为边的格点三角形(顶点在格点上).
 (1)、在图1中画一个直角三角形 , 使点P在的内部(不包括边界).(2)、在图2中画一个等腰三角形 , 使点P在一边的中垂线上.19. 已知:如图,在中,于点 , 为上一点,且 , . 猜想与的关系,并说明理由.
(1)、在图1中画一个直角三角形 , 使点P在的内部(不包括边界).(2)、在图2中画一个等腰三角形 , 使点P在一边的中垂线上.19. 已知:如图,在中,于点 , 为上一点,且 , . 猜想与的关系,并说明理由. 20. 如图,在中,于点 , 垂直平分 , 交于点 , 交于点 , 连接 , 且 .
20. 如图,在中,于点 , 垂直平分 , 交于点 , 交于点 , 连接 , 且 . (1)、求证:平分 .(2)、若 , 求的度数.21. “劳动基地”是培养学生劳动意识和创新精神的重要平台,某校在校园一角开辟了一块四边形的“劳动基地”,如图,经过测量得知:∠B=90°,AB=6m , BC=8m , CD=24m , AD=26m .
(1)、求证:平分 .(2)、若 , 求的度数.21. “劳动基地”是培养学生劳动意识和创新精神的重要平台,某校在校园一角开辟了一块四边形的“劳动基地”,如图,经过测量得知:∠B=90°,AB=6m , BC=8m , CD=24m , AD=26m . (1)、连接AC , 判断△ACD的形状并说明理由;(2)、若在该基地上种植蔬菜,每平方米需要费用3元,试问种满这块基地共需费用多少元?22. 【问题情境】某数学兴趣小组想测量学校旗杆的高度.
(1)、连接AC , 判断△ACD的形状并说明理由;(2)、若在该基地上种植蔬菜,每平方米需要费用3元,试问种满这块基地共需费用多少元?22. 【问题情境】某数学兴趣小组想测量学校旗杆的高度.【实践发现】数学兴趣小组实地勘察发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知,
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1米;
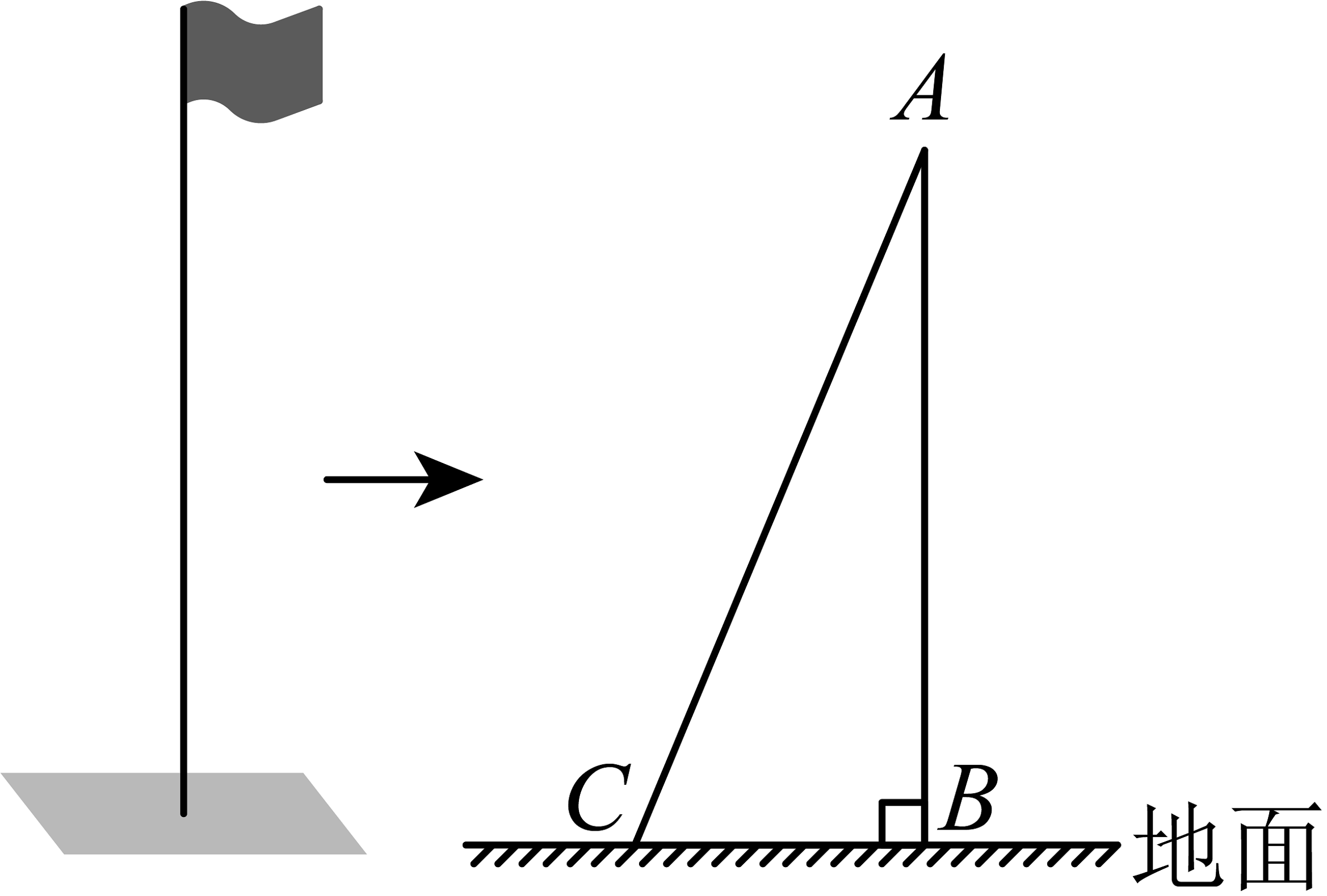
第二步,把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5米;
【问题解决】设旗杆的高度为x米,通过计算请你求旗杆的高度.
 23. 在学习勾股定理时,我们学会运用图(Ⅰ)验证它的正确性;图中大正方形的面积可表示为: , 也可表示为: ,
23. 在学习勾股定理时,我们学会运用图(Ⅰ)验证它的正确性;图中大正方形的面积可表示为: , 也可表示为: ,即由此推出勾股定理 , 这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
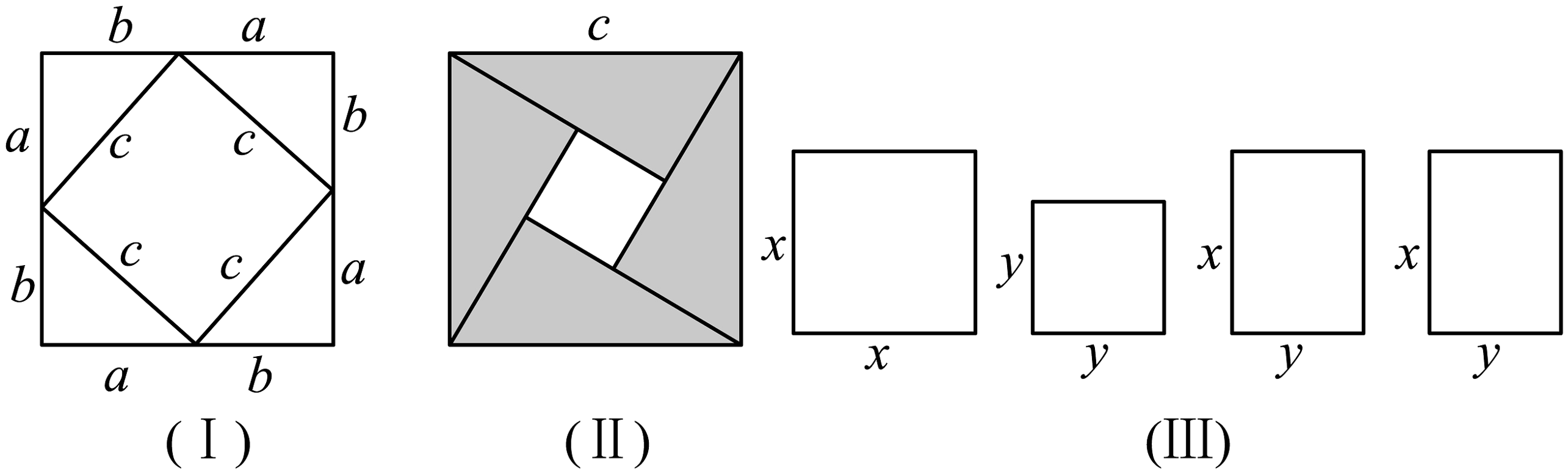 (1)、请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);(2)、请你用(III)提供的图形进行组合,用组合图形的面积表达式验证;(3)、请你自己设计图形的组合,用其面积表达式验证: .24. 定义:把斜边重合,且直角顶点不重合的两个直角三角形叫做共边直角三角形.
(1)、请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等);(2)、请你用(III)提供的图形进行组合,用组合图形的面积表达式验证;(3)、请你自己设计图形的组合,用其面积表达式验证: .24. 定义:把斜边重合,且直角顶点不重合的两个直角三角形叫做共边直角三角形. (1)、概念理解:如图1.在和中, , , , , , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连接AD , 求证:平分 .
(1)、概念理解:如图1.在和中, , , , , , 说明和是共边直角三角形.(2)、问题探究:如图2,和是共边直角三角形,E、F分别是BC、AD的中点,连接EF , 求证 .(3)、拓展延伸:如图3,和是共边直角三角形,且 , 连接AD , 求证:平分 .