人教版七（上）第一章有理数单元测试培优卷

试卷更新日期：2025-10-05 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 四个有理数 $- 3$ ， 1，0， $- 1$ ，其中最小的数是（）

A、 $- 3$ B、1 C、0 D、 $- 1$

查看试题解析
2. $| - \frac{1}{3} |$ 的相反数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、-3

查看试题解析
3. 化学老师在实验室中发现了四个因操作不规范沾染污垢或被腐蚀的砝码，经过测量，超出标准质量的部分记为正数、不足的部分记为负数，它们中质量最接近标准的是（）

A、 B、 C、 D、

查看试题解析
4. 世界上最早记载负数的是中国古代的数学著作《九章算术》，负数可以用来表示具有相反意义的量．规定盈利为正，如盈利 30 元，记作 +30 元，那么－50 元表示（）

A、支出 50 元
B、收入 50 元
C、盈利 50 元
D、亏损 50 元

查看试题解析
5. 在数轴上，点A ， B在原点O的同侧，分别表示数a ， 1，将点A向左平移3个单位长度，得到点C ．若点C与点B互为相反数，则a的值为（）

A、3 B、2 C、 $- 1$ D、0

查看试题解析
6. 有理数a，b，c，d在数轴上的对应点的位置如图所示．若|a-c|=10，|a-d|=12，|b-d|=9，则|b-c|的值是（）．

A、5 B、6 C、7 D、10

查看试题解析
7. 在数轴上，把表示 $- 2$ 的点沿着数轴移动7个单位长度得到的点所表示的数是（）

A、5 B、 $- 9$ C、 $\pm 5$ D、5或 $- 9$

查看试题解析
8. 如果 $| a | = - a$ ，下列成立的是（）

A、 $a > 0$ B、 $a < 0$ C、 $a \geq 0$ D、 $a \leq 0$

查看试题解析
9. 数轴上表示整数的点称为整点，某数轴的单位长度是1厘米，若在这个数轴上随意画出一条长为2008厘米的线段AB ，则线段AB盖住的整点是（　　）

A、2006个或2007个 B、2007个或2008个 C、2008个或2009个 D、2009个或2010个

查看试题解析
10. 在数轴上任取一条长度为 $2013 \frac{1}{2013}$ 的线段，则此线段在这条数轴上最多能盖住的整数点的个数是（　　）

A、2012 B、2013 C、2014 D、2015

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 比较大小： $- (+ \frac{1}{3})$ $- | - \frac{1}{2} |$ ．（填“>”“<”或“=”）

查看试题解析
12. 如果 $|x| = |- 5|$ ，那么 $x =$ ．

查看试题解析
13. 一把刻度尺的部分在数轴上的位置摆放如图所示，若刻度尺上的刻度“ $4 cm$ ”和“ $1 cm$ ”分别对应数轴上的 $0$ 和 $2$ ，现将该刻度尺沿数轴向右平移 $3$ 个单位，则刻度尺上 $6.1 cm$ 对应数轴上的数为．

查看试题解析
14. 一组按规律排列的数： $- 2$ ， $\frac{4}{3}$ ， $- \frac{8}{5}$ ， $\frac{16}{7}$ ， $- \frac{32}{9}$ ， $\dots$ ，其中第 $7$ 个数是，第 $n$ （ $n$ 为正整数）个数是．

查看试题解析
15. 电影《哈利•波特》中，小哈利波特穿越墙进入“ $9 \frac{3}{4}$ 站台”的镜头（如示意图的Q站台），构思奇妙，能给观众留下深刻的印象．若A、B站台分别位于﹣ $\frac{2}{3}$ ， $\frac{8}{3}$ 处，AP=2PB，则P站台用类似电影的方法可称为“站台”．

查看试题解析

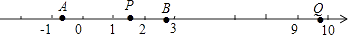
三、

16. 如果一个问题中出现具有相反意义的量，就可以用正数和负数分别表示它们．例如：用 $+ 60$ 千米表示向东行驶60千米，那么下列各数分别表示什么？

(1)、 $+ 800$ 千米；

(2)、 $- 50$ 千米；

(3)、0千米．

查看试题解析
17. 画一条数轴，把下列各数和它们的相反数在数轴上表示出来，并比较它们的大小，用“ $<$ ”号连接起来．
$- 1 \frac{1}{2}$ ， 0， ${(- 2)}^{2}$ ， $|- 1|$

查看试题解析
18. 为积极倡导“阳光体育”运动，某班派6名同学参加“一分钟跳绳”比赛，负责记录成绩的嘉嘉以160次为标准，超出的次数记为正数，不足的次数记为负数，其中5名同学的成绩记录（单位：次）为： $- 10 ， + 4 ， + 11 ， - 9 ， + 1$ ．

(1)、求这5名同学的最好成绩与最差成绩相差多少次？

(2)、若这6名同学的平均成绩超过了160次，求剩下的那名同学的成绩最少为多少．

查看试题解析
19. 如图，在数轴上标出的所有点中，任意相邻两点间的距离都相等．已知点E表示原点，点G表示的有理数是8．

(1)、点A表示的数为，点F表示的数为；

(2)、在数轴上标出的所有点中，表示的数互为相反数的两点为；

(3)、点P为数轴上一点，且表示的数是整数，若点P到点C的距离与点P到点F的距离之和为12，则这样的点P共有多少个？请说明理由．

(4)、数轴上有两个点M，N，点M到点D的距离为5，点N到点D的距离是3.7，则点M，N之间的距离为多少？请说明理由．

查看试题解析
20. 如图，在一条不完整的数轴上从左到右依次有A，B，C三个点，其中A到B的距离为3，B到C的距离为8，设A，B，C所对应的数的和为m．

(1)、若以B为原点，求数轴上A，C所表示的数，并求出此时m的值；

(2)、若原点到B的距离为3，求m的值．

查看试题解析
21. 如图一根木棒放在数轴上，数轴的1个单位长度为1cm，木棒的左端与数轴上的点A重合，右端与点B重合．

(1)、若将木棒沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为20；若将木棒沿数轴向左水平移动，则当它的右端移动到A点时，则它的左端在数轴上所对应的数为5，由此可得到木棒长为___________cm．

(2)、图中点A所表示的数是___________，点B所表示的数是___________．

(3)、由题（1）（2）的启发，请你能借助“数轴”这个工具帮助小红解决下列问题：一天，小红去问曾当过数学老师现在退休在家的爷爷的年龄，爷爷说：“我若是你现在这么大，你还要35年才出生；你若是我现在这么大，我已经130岁，是老寿星了，哈哈！”，请求出爷爷现在多少岁了？

查看试题解析
22. 阅读下面的材料：
根据绝对值的几何意义，我们知道 $|5 - 3|$ 表示5、3在数轴上对应的两点间的距离； $|5 + 3| = |5 - (- 3)|$ ，所以 $|5 + 3|$ 表示5、 $- 3$ 在数轴上对应的两点之间的距离； $|5| = |5 - 0|$ ，所以 $|5|$ 表示5在数轴上对应的点到原点的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B两点之间的距离可以表示为 $|A B| = |a - b|$ ．
回答下列问题：

(1)、数轴上表示6与 $- 9$ 的两点之间的距离是；数轴上表示x与2的两点之间的距离是．

(2)、若 $|x - 3| = 3$ ，则 $x =$ ．

(3)、满足 $|x + 2| + |x - 3| = 5$ 的整数x有个．

(4)、当 $a =$ 时，代数式 $|x + a| + |x - \frac{1}{2}|$ 的最小值是3．

查看试题解析
23. 综合运用
同学们，我们在教材中学习过绝对值的概念：在数轴上，一个数a所对应的点与原点的距离叫做这个数的绝对值，记作 $| a |$ ．如 $| - 3 |$ 指数轴上点 $- 3$ 到原点的距离， $| - 3 |$ 也可以写成 $| - 3 - 0 |$ ；数轴上表示数 $- 3$ 的点与表示数2的点的距离可记作 $| - 3 - 2 |$ ，值为5．也就是说，在数轴上，如果A点表示的数记为a ， B点表示的数记为b ，则A、B两点间的距离就可记作 $| a - b |$ ．利用数形结合思想回答下列问题：

(1)、数轴上表示2和7的两点之间的距离的值是；数轴上表示x与 $- 2$ 的两点之间的距离可记作，如果这两点之间的距离为3，那么 $x =$ ；

(2)、利用数轴，找出所有符合条件的整数x ，使 $| x - 2 | + | x + 1 | = 3$ ；

(3)、若x表示有理数，直接写出： $| x - 1 | + | x - 2 | + | x - 3 | + | x - 4 | + \cdot \cdot \cdot + | x - 2022 | + | x - 2023 |$ 的最小值．

查看试题解析

人教版七（上） 第一章 有理数 单元测试培优卷

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

二、填空题：本大题共5小题，每小题3分，共15分.

三、

人教版七（上）第一章有理数单元测试培优卷