第六章《平明图形的初步认识》提升卷—苏科版数学七（上）单元测

试卷更新日期：2025-10-05 类型：单元试卷

进入出卷网下载

一、选择题：本大题共8小题，每小题3分，共24分.在每小题给出的四个选项中，只有一个是正确的.每小题选对得3分，选错、不选或多选，均不得分.

1. 下列几何图形与相应语言描述相符的是（）

A、如图①，延长线段 $A B$ 到点 $C$ B、如图②，点 $B$ 在射线 $C A$ 上 C、如图③，直线 $A B$ 的延长线与直线 $C D$ 的延长线相交于点 $P$ D、如图④，射线 $C D$ 和线段 $A B$ 没有交点

查看试题解析
2. 下列说法中，错误的是（）

A、两点之间的线段最短 B、如果 $∠ α = 53 ° 38^{'}$ ，那么 $∠ α$ 余角的度数为 $36 ° 22^{'}$ C、一个锐角的余角比这个角的补角小 D、互补的两个角一个是锐角一个是钝角

查看试题解析
3. 某班50名同学分别站在公路的A，B 两点处，A，B 两点相距1000米，A 处有30人，B处有20人.要让两处的同学走到一起，并且使所有同学走的路程总和最小，那么集合地点应选在（）.

A、A 点处 B、线段 AB 的中点处 C、线段AB上，距A 点 $\frac{1000}{3}$ 米处 D、线段AB 上，距A 点 400米处

查看试题解析
4. 平面内的9条直线任意2条都相交，交点数最多有m个，最少有n个，则m+n等于( )

A、36 B、37 C、38 D、39

查看试题解析
5. 在下图中，∠1＝∠2，能判断AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，线段 AB 所在的直线与线段CD 所在的直线互相垂直，若∠A=30°，∠D=50°，则∠E+∠F=（）.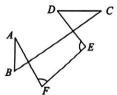

A、190° B、180° C、170° D、160°

查看试题解析
7. 将一副三角板按如图放置， $∠ B A C = ∠ D A E = 90 °$ ， $∠ B = 45 °$ ， $∠ E = 60 °$ ，则：① $∠ 1 = ∠ 3$ ；② $∠ C A D + ∠ 2 = 180 °$ ；③如果 $∠ 2 = 30 °$ ，则有 $A C ∥ D E$ ；④如果 $∠ 2 = 45 °$ ，则有 $B C ∥ A D$ ．上述结论中正确的个数是（）

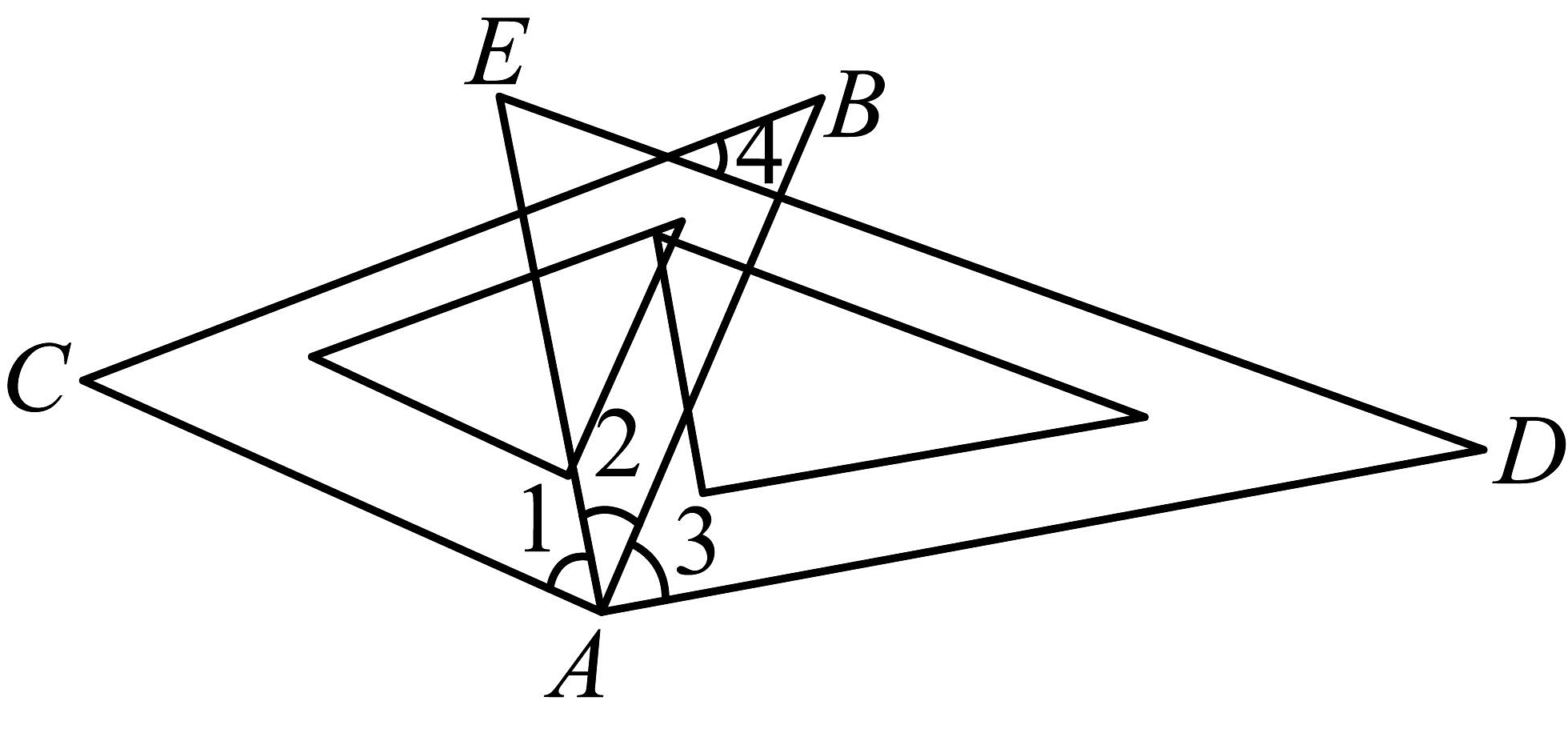A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，点O在直线 $A B$ 上，过O作射线 $O C$ ， $∠ B O C = 100 °$ ，一直角三角板的直角顶点与点O重合，边 $O M$ 与 $O B$ 重合，边 $O N$ 在直线 $A B$ 的下方．若三角板绕点O按每秒 $10 °$ 的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直线 $O N$ 恰好平分锐角 $∠ A O C$ ，则t的值为（）

A、5 B、4 C、5或23 D、4或22

查看试题解析

二、填空题：本大题共10小题，每小题3分，共30分.只要求填出最后结果.

9. 新昌挂岩岭隧道和上角坪隧道 $A - B$ （示意图如图）通过把部分道路取直以缩短路程，其中蕴含的数学原理是．

查看试题解析
10. 如图，在一张零件图纸中， $A D = 83 mm$ ， $A B = 8 mm$ ， $C D = 23 mm$ ，则 $B C$ 的长为．

查看试题解析
11. 如图，已知∠AOB=∠COD=90°，∠COE=∠BOE，点 F 为OE 反向延长线上一点（图中所有角均指小于180°的角），给出下列结论：
①∠AOE=∠DOE；②∠AOD+∠COB=180°；③∠COB-∠AOD=90°；④∠COE+∠BOF=180°.
其中结论正确的是.

查看试题解析
12. 如图，某海域有三个小岛A，B，O，在小岛O处观测到小岛A在它北偏东 $60 °$ 的方向上，观测到小岛B在它南偏东 $38 °$ 的方向上，则 $∠ A O B$ 的度数是．

查看试题解析
13. 已知线段 $A B$ ， $C D$ 相交于点 $O$ （不与端点重合）， $O E$ 平分 $∠ A O D$ ， $O F ⊥ C D$ 于点 $O$ ，若 $∠ A O C ： ∠ A O E = 1 ： 2$ ，则 $∠ B O F$ 的度数为．

查看试题解析
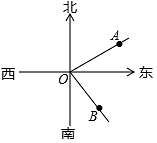14. 一个多边形截去一个（三角形状的）角后，形成另一个多边形，其内角和是3060°，则原多边形是边形.

查看试题解析
15. 如图，一副三角尺按不同的位置摆放，摆放位置中 $∠ α = ∠ β$ 的图形有．（填序号）

查看试题解析
16. 某市为了方便市民绿色出行，推出了共享单车服务，如图1，某品牌共享单车放在水平地面上，图2是其示意图，其中 $A B ， C D$ 都与地面 $l$ 平行， $∠ B C D = 72 °$ ， $∠ B A C = 45 °$ ，当 $∠ M A C$ 为 $°$ 时， $A M$ 与 $C B$ 平行．

查看试题解析
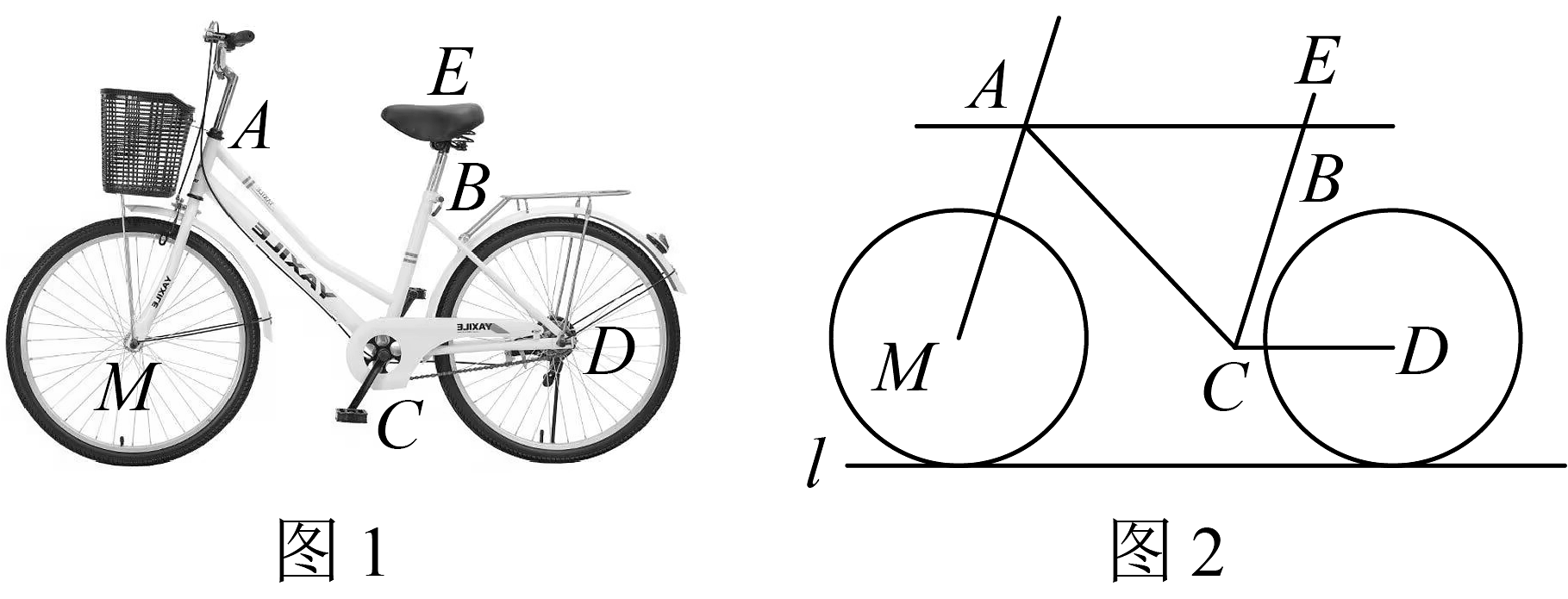17. 如图，在科学《光的反射》活动课中，小明同学将支架平面镜放置在水平桌面 $M N$ 上，镜面 $A B$ 的调节角 $∠ A B M = α (0 ° < α < 75 ° 且 α \neq 60 °)$ ，激光笔发出的光束 $D G$ 射到平面镜上后，形成反射光束 $G H$ ，发现 $∠ A G H = ∠ B G P$ ，若激光笔与水平天花板（直线 $E F$ ）的夹角 $∠ E P G = 30 °$ ，则 $G H$ 与天花板所形成的角 $∠ P H G$ 的度数可用含 $α$ 的代数式表示为．

查看试题解析
18. “皮克定理”是用来计算顶点在整点的多边形面积的公式，公式表达式为S= $a + \frac{b}{2} - 1,$ 孔明只记得公式中的S 表示多边形的面积，a和b 中有一个表示多边形边上（含顶点）的整点个数，另一个表示多边形内部的整点个数，但不记得究竟是a 还是b 表示多边形内部的整点个数，请你选择一些特殊的多边形（如图①）进行验证，得到公式中表示多边形内部的整点个数的字母是；并运用这个公式求得图②中多边形的面积是.

查看试题解析

三、解答题：本大题10小题，共96分.

19. 如图，已知平面内有四个点 $A$ ， $B$ ， $C$ ， $D$ ．根据下列语句按要求画图．

(1)、连接 $A B$ ；

(2)、作射线 $A D$ ，并在线段 $A D$ 的延长线上用圆规截取 $D E = A B$ ；

(3)、作直线 $B C$ 与射线 $A D$ 交于点 $F$ ．
观察图形发现，线段 $A F + B F > A B$ ，得出这个结论的依据是：．

查看试题解析
20. 用尺规完成下列作图：

(1)、如图(1)，已知∠α，∠β，且∠α>∠β，作∠DEF，使∠DEF=∠α-∠β；

(2)、如图(2)，以点B为顶点、射线BC为一边，作∠EBC，使∠EBC=∠A。

查看试题解析
21. 操作题．
（1）如图是一个正方形网格，在此网格中有直线 $A B$ 与点 $C$ ．请按下列要求画图：
①画直线 $C D ∥ A B$ ；
②画直线 $C E ⊥ A B$ ，垂足为点 $F$ ．
（温馨提示：要标明字母呦）
（2）作图题（尺规作图，要求：不写作法，保留作图痕迹）
如图，已知 $P$ 是 $∠ B A C$ 的边 $A B$ 上不同于 $A$ 的一点，经过点 $P$ 请作出 $A C$ 的平行线 $P Q$ ．

查看试题解析
22. 如图. $A D ∥ B C ， ∠ 1 = ∠ B ， ∠ 2 = ∠ 3$ .

注：本题第（1）、（2）小题在下面的解答过程的空格内填写理由或数学式；第（3）小题要写出解题过程.

(1)、试说明： $E B ∥ D C$ ；
∵ $A D ∥ B C$ ，（已知）

∴ $∠ B = ∠$       ▲      （             ）

又∵ $∠ 1 = ∠ B$ ，（已知）

∴ $∠ 1 = ∠$       ▲      （等量代换）

∴      ▲       $∥$       ▲      （             ）

(2)、 $A C$ 与 $E D$ 的位置关系如何?为什么?
$A C$ 与 $E D$ 的位置关系是：                ，理由如下：
∵ $A D ∥ B C$ ，（已知）

∴ $∠ 3 = ∠$       ▲      （              ）

又∵ $∠ 2 = ∠ 3$ ，（已知）

∴∠      ▲      =∠      ▲      （等量代换）

∴      ▲      //      ▲      .（               ）

(3)、 $∠ B E D$ 与 $∠ A C D$ 相等吗?请说明理由.

查看试题解析
23. 定义：若 $α - β = 90 °$ ，且 $90 ° < α < 180 °$ ，则我们称 $β$ 是 $α$ 的差余角．例如：若 $α = 110 °$ ，则 $α$ 的差余角 $β = 20 °$ ．如图1，点 $O$ 在直线 $A B$ 上， $O C$ 是 $A B$ 上方的一条射线，且 $∠ B O C < 90 °$ ．

(1)、若 $∠ B O C$ 是 $∠ A O C$ 的差余角，求 $∠ B O C$ ；

(2)、将直角三角尺 $D O E$ 按如图2放置，使得直角顶点与 $O$ 点重合，且 $O D$ 平分 $∠ B O C$ ，
①判断 $∠ A O C$ 和 $∠ A O E$ 的数量关系，并说明理由；
②图中 $∠ A O D$ 的差余角有哪些？请说明理由；

(3)、将直角三角尺 $D O E$ 自图3位置（三角尺一边 $O D$ 在 $O B$ 上）开始绕直角顶点 $O$ 顺时针转动，当 $∠ C O E$ 是 $∠ A O E$ 的差余角时，请直接写出此时 $∠ C O E$ 与 $∠ B O D$ 的数量关系．

查看试题解析
24. 综合与实践.
问题情境：在探索多边形的内角与外角关系的活动中，同学们经历了观察、猜想、实验、计算、推理、验证等过程，提出了问题，请解答：

(1)、若四边形的一个内角的度数是 $a$ .
①求和它相邻的外角的度数(用含 $a$ 的代数式表示)；
②求其它三个内角的和（用含 $a$ 的代数式表示）

(2)、若一个 $n$ 边形 $(n > 3)$ ，除了一个内角，其余内角的和为 $92 0^{°}$ ，求 $n$ 的值.

(3)、深入探究
探究 $n$ 边形 $(n > 3)$ 的一个外角与和它不相邻的 $(n - 1)$ 个内角的和之间满足的等量关系，说明理由.

查看试题解析
25. 如图1，大课间的广播操展让我们充分体会到了一种整体的图形之美，洋洋和乐乐想从数学角度分析下如何能让班级同学们的广播操做得更好，他们搜集了标准广播操图片进行讨论，如图2，为了方便研究，定义两手手心位置分别为A ， B两点，两脚脚跟位置分别为C ， D两点，定义A ， B ， C ， D平面内O为定点，将手脚运动看作绕点O进行旋转：

(1)、填空：如图2，A ， O ， B三点共线，且∠AOC＝∠BOC ，则∠AOC＝°；

(2)、第三节腿部运动中，如图3，洋洋发现，虽然A ， O ， B三点共线，却不在水平方向上，且∠AOD：∠BOC＝3：2．他经过计算发现，∠AOC﹣ $\frac{2}{3}$ ∠BOD的值为定值，请判断洋洋的发现是否正确，如果正确请求出这个定值，如果不正确，请说明理由；

(3)、第四节体侧运动中，乐乐发现，两腿左右等距张开且∠COD＝30°，开始运动前A、O、B三点在同一水平线上，OA、OB绕点O顺时针旋转，OA旋转速度为50°/s ， OB旋转速度为25°/s ，当OB旋转到与OD重合时，运动停止，如图4．
①运动停止时，直接写出∠AOD＝　▲　；
②请帮助乐乐求解运动过程中∠AOC与∠BOE的数量关系．

查看试题解析
26. 综合与实践
【问题情境】
自行车的尾灯自身并不发光，但当强光照射到尾灯上时光线会被强烈地反射回去，从而起到提醒汽车驾驶员的目的. 这一效果正是利用了角反射器的原理. 最简单的角反射器是由两个互相垂直的平面镜组成的.
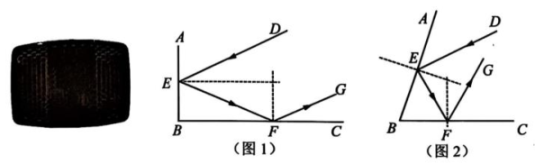
【数学探究】
如图，入射光线DE经过两次反射后，得到光线FG，已知 $∠ A E D = ∠ B E F$ ， $∠ E F B = ∠ G F C$ .

(1)、如图1，AB，BC是两个互相垂直的平面镜， $∠ A B C = 9 0^{°}$ ，
①若 $∠ A E D = 7 0^{°}$ ，求 $∠ G F C$ 的度数.
②试判断入射光线DE和反射光线FG是否平行，并说明理由.

(2)、如图2，改变镜子位置，设平面镜AB，BC的夹角 $∠ A B C = α (α < 9 0^{°})$ ， $∠ A E D = β$ ， $9 0^{°} < α + β < 18 0^{°}$ ，求 $∠ D E F + ∠ E F G$ 的值（用含有 $α$ 或 $β$ 的代数式表示）.

查看试题解析
27. 【问题初探】
（ $1$ ）数学活动课上，王老师给出如下问题：如图 $1$ ， $A B ∥ C D$ ，点 $E$ 在 $A B$ ， $C D$ 之间且点 $E$ 在点 $A$ 右侧，求证： $∠ A E C = ∠ B A E + ∠ D C E$ ；
【类比探究】
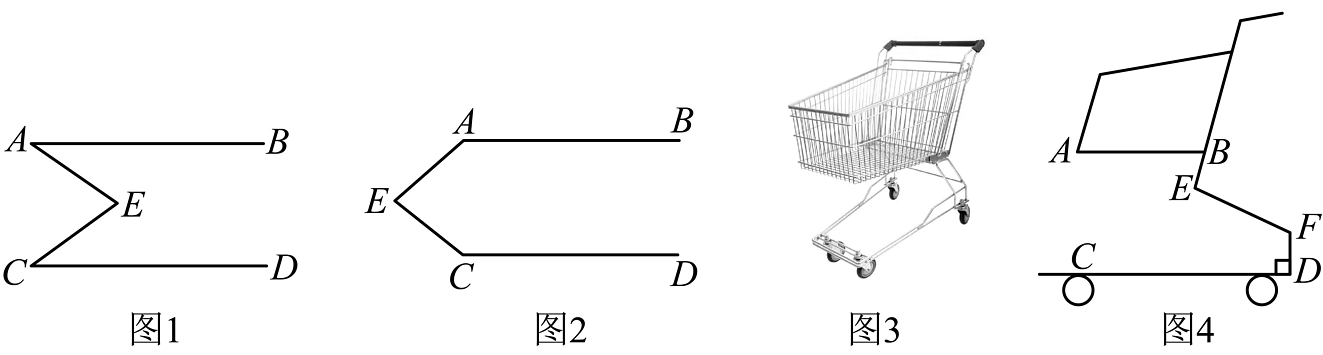
（ $2$ ）李明对王老师给出的问题进行了改编：如图 $2$ ， $A B ∥ C D$ ，点 $E$ 在 $A B$ ， $C D$ 之间且点 $E$ 在点 $A$ 左侧，直接写出 $∠ A E C$ ， $∠ B A E$ ， $∠ D C E$ 之间的数量关系；
【学以致用】
（ $3$ ）如图 $3$ 是超市购物车，图 $4$ 是其侧面示意图，已知 $A B ∥ C D$ ， $F D ⊥ C D$ ，测量得知 $∠ A B E = 75 °$ ， $∠ D F E = 115 °$ ，求 $∠ B E F$ 的度数．

查看试题解析
28. 阅读下列材料，并完成相应任务．
关于同一种多边形的平面密铺
平面密铺的定义：平面密铺是指用一些形状大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠的铺成一片，这就是平面图形的密铺，又称做平面图形的镶嵌．
任务一：探究同一种正多边形的密铺．
如图1，通过拼图发现正方形、正六边形都可以进行密铺，此时公共顶点处的几个角正好拼成了一个周角．
问题① 铺的条件为：当公共顶点处所有角的和为___________ $°$ ，并使相等的边重合时，该图形就可以进行密铺．
问题② 认为正五边形可以进行密铺吗？并说明理由．
任务二：探究同一种一般多边形的密铺
经过同学们动手实验，每小组画出自己小组的拼接图，如图2．
问题③ 观察图2，可以发现任意__________和任意__________都可以单独密铺．
经过研究发现三对对边平行的六边形可以单独密铺，人们借助六边形的密铺，发现虽然正五边形不能进行密铺，但有些特殊五边形可以进行密铺，从此展开了对一般五边形的密铺探究．
目前可以密铺的凸五边形共有15种，如图3为其中一种五边形的密铺图．
问题④ 图4为图3中抽象出的一个五边形，其中 $∠ C = ∠ E = 90 °$ ， $∠ A = ∠ B = ∠ D$ ，则 $∠ A$ 的度数为__________．

查看试题解析