第五章《直角三角形》提升卷—湘教版数学八(上)单元分层测
试卷更新日期:2025-10-05 类型:单元试卷
一、选择题:本题共10小题,每小题3分,共30分
-
1. 在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,下列条件中不能判定Rt△ABC≌Rt△A′B′C′的是( )A、AC=A′C′,∠B=∠B′ B、∠A=∠A′,∠B=∠B′ C、AB=A′B′,AC=A′C′ D、AB=A′B′,∠A=∠A′2. 直角三角形中两个锐角的平分线相交所成的钝角的度数为( )A、 B、 C、 D、 或3. △ABC中,AB=15,AC=13,高AD=12,则△ABC的周长是( )A、42 B、32 C、42或32 D、42或374. 如图,已知平分 , , , 于点D,于点E.如果点M是的中点,则的长是( )
 A、1 B、2 C、3 D、45. 如图,在中, , 且三点共线,点是线段上任意一点,连接 , 则的最小值为( )
A、1 B、2 C、3 D、45. 如图,在中, , 且三点共线,点是线段上任意一点,连接 , 则的最小值为( ) A、8 B、10 C、12 D、166. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形与正方形 . 连接 , 相交于点O、与相交于点P.若 , 则的值是( )
A、8 B、10 C、12 D、166. 如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形与正方形 . 连接 , 相交于点O、与相交于点P.若 , 则的值是( ) A、 B、 C、 D、7. 如图,在A村与村之间有一座大山,原来从A村到村,需沿道路()绕过村庄间的大山,打通A , 间的隧道后,就可直接从A村到村.已知 , , 那么打通隧道后从A村到村比原来减少的路程为( )
A、 B、 C、 D、7. 如图,在A村与村之间有一座大山,原来从A村到村,需沿道路()绕过村庄间的大山,打通A , 间的隧道后,就可直接从A村到村.已知 , , 那么打通隧道后从A村到村比原来减少的路程为( ) A、 B、 C、 D、8. 如图, , , 将沿翻折,使得点C与点B重合.若 , , 则折痕的长为( )
A、 B、 C、 D、8. 如图, , , 将沿翻折,使得点C与点B重合.若 , , 则折痕的长为( ) A、4 B、 C、5 D、9. 某同学类比勾股定理的证明过程,利用三个含有的全等三角形纸片(如图①)拼成一个正三角形(如图②),即 . 连接 , , , 若长是2,的面积是 , 则的面积是( )
A、4 B、 C、5 D、9. 某同学类比勾股定理的证明过程,利用三个含有的全等三角形纸片(如图①)拼成一个正三角形(如图②),即 . 连接 , , , 若长是2,的面积是 , 则的面积是( ) A、 B、 C、 D、10. 如图,在中,平分交于点 , 作 , , 垂足分别为、 , 若 , 则下列四个结论:①;②;③;④ . 其中结论正确的序号有( )
A、 B、 C、 D、10. 如图,在中,平分交于点 , 作 , , 垂足分别为、 , 若 , 则下列四个结论:①;②;③;④ . 其中结论正确的序号有( ) A、①②③ B、②③④ C、①③④ D、①②③④
A、①②③ B、②③④ C、①③④ D、①②③④二、填空题:本题共8小题,每小题3分,共24分
-
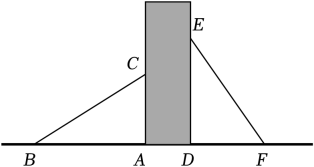
11. 如图,某小区广场有两个长度相等的滑梯靠在一面墙上,已知左边滑梯水平方向的长度AB与右边滑梯的高度DE相等.若右边滑梯与地面的夹角∠DFE=55°,则∠ABC的度数为°.
 12. 如图,在中, , , 是高,若 , 则 .
12. 如图,在中, , , 是高,若 , 则 . 13. 如图,在四边形中, , E为对角线的中点,连接 , , , 若 , 则.
13. 如图,在四边形中, , E为对角线的中点,连接 , , , 若 , 则. 14. 如图,在的网格中, .
14. 如图,在的网格中, . 15. 如图,一架米长的梯子斜靠在一竖直的墙上,这时梯足到墙底端的距离为米,如果梯子的顶端沿墙下滑米,那么梯足将外移米.
15. 如图,一架米长的梯子斜靠在一竖直的墙上,这时梯足到墙底端的距离为米,如果梯子的顶端沿墙下滑米,那么梯足将外移米. 16. 如图,是直线上一点, , 平分 , 交于点 , , 于点 , 则 .
16. 如图,是直线上一点, , 平分 , 交于点 , , 于点 , 则 .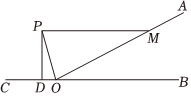 17. 如图,在 中, 于点 于点 ,并且点 是 的中点,的周长是 ,则 的长是。
17. 如图,在 中, 于点 于点 ,并且点 是 的中点,的周长是 ,则 的长是。 18. 如图,在中, , , , 点在上,过点作的垂线,分别交射线 , 线段于点 , , 连接 , 恰好平分 , 则线段的长是 .
18. 如图,在中, , , , 点在上,过点作的垂线,分别交射线 , 线段于点 , , 连接 , 恰好平分 , 则线段的长是 .
三、解答题:本题共8小题,共66分
-
19. 图①、图②、图③均为的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点称为格点,按下列要求作图:
 (1)、在图①中画出 , 使三个顶点均在格点上且;(2)、在图②中画出 , 使三个顶点均在格点上且;(3)、在图③中画出 , 使三个顶点均在格点上且 .20. 如图,在中,是边上的高线,是边上的中线,于G, , 连接 .
(1)、在图①中画出 , 使三个顶点均在格点上且;(2)、在图②中画出 , 使三个顶点均在格点上且;(3)、在图③中画出 , 使三个顶点均在格点上且 .20. 如图,在中,是边上的高线,是边上的中线,于G, , 连接 . (1)、求证:;(2)、已知 , 求的面积.21. 如图,在中, , 、、分别是、、的中点,连结、 , 求证: .
(1)、求证:;(2)、已知 , 求的面积.21. 如图,在中, , 、、分别是、、的中点,连结、 , 求证: .
针对这道题,三位同学进行了如下讨论--
小胡:“需要利用全等证明.”
小吴:“要证中线相等,我想到了直角三角形.”
小明:“我觉得你们都对,但还有别的方法.”
请你结合上述讨论,选择恰当的方法完成证明.
22. 拖拉机行驶过程中会对周围产生较大的噪声影响.如图,有一台拖拉机沿公路AB由点A向点B行驶,已知点C为一所学校,且点C与直线AB上两点A,B的距离分别为150m和200m,又AB=250m,拖拉机周围130m以内为受噪声影响区域. (1)、学校C会受噪声影响吗?为什么?(2)、若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?23. 在中,平分交于 .
(1)、学校C会受噪声影响吗?为什么?(2)、若拖拉机的行驶速度为每分钟50米,拖拉机噪声影响该学校持续的时间有多少分钟?23. 在中,平分交于 . (1)、如图1,的两边分别与、相交于M、N两点,过D作于F, , 证明:;(2)、如图2,若 , , , , , 求四边形的周长.24. 如图,在中, , 点是边的中点,以为底边向上作等腰 , 使得 , 交于点 ,
(1)、如图1,的两边分别与、相交于M、N两点,过D作于F, , 证明:;(2)、如图2,若 , , , , , 求四边形的周长.24. 如图,在中, , 点是边的中点,以为底边向上作等腰 , 使得 , 交于点 , (1)、若 , 求度数;(2)、若 .
(1)、若 , 求度数;(2)、若 .①求证:;
②设 , 求的长(用含的代数式表示).
25. 赵爽在《周髀算经》中介绍了“勾股圆方图”,亦称“赵爽弦图”(如图1),并根据该图证明了勾股定理.弦图之美,美在简约而深厚,经典而久远,被誉为“中国数学界的图腾”. (1)、“勾股定理”用文字叙述是__________________;(2)、类比“赵爽弦图”构造出图2:为等边三角形,、、围成的是等边三角形.点D、E、F分别是、、的中点,若的面积为2,求的面积;(3)、在长方形内部嵌入了3个全等的“赵爽弦图”(如图3),其中点M、N、P、Q分别在长方形的边、、、上,当 , 时,求小正方形的边的长度;26. 综合与实践:小嵊与小州两个同学在学习了“直角三角形全等的判定”后,对数学中重要的学习方法“构造法”,展开了课后探究.
(1)、“勾股定理”用文字叙述是__________________;(2)、类比“赵爽弦图”构造出图2:为等边三角形,、、围成的是等边三角形.点D、E、F分别是、、的中点,若的面积为2,求的面积;(3)、在长方形内部嵌入了3个全等的“赵爽弦图”(如图3),其中点M、N、P、Q分别在长方形的边、、、上,当 , 时,求小正方形的边的长度;26. 综合与实践:小嵊与小州两个同学在学习了“直角三角形全等的判定”后,对数学中重要的学习方法“构造法”,展开了课后探究.【情景再现】
已知,如图1,在和中, , , .
下面是用“构造法”证明两个直角三角形全等的部分过程.
证明:如图1,延长至D,使 , 连接 .
因为(已知), ,
所以
所以(全等三角形的对应边相等).
…
所以
所以

【实践解决】
(1)、请结合“情景再现”的证明过程,把“…”的部分补充完整;(2)、小嵊进行了如下的思考:如图2,和都是等腰直角三角形,且 . 连接 , 若 , , , 求的长;(3)、小州结合“构造法“进行进一步探究:如图3,是等腰直角三角形, , P是外一点, , , , 求线段的长.