第四章《三角形》基础卷—湘教版数学八(上)单元分层测
试卷更新日期:2025-10-05 类型:单元试卷
一、选择题:本题共10小题,每小题3分,共30分
-
1. 下列每组数分别是三根小木棒的长度,用它们首尾相连能摆成三角形的是( )A、 , 5,7 B、3,4,8 C、1, , D、5,5,102. 下面四个图形中,线段BE是⊿ABC的高的图是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列选项中可以用来说明命题“若x2>1,则x>1”是假命题的反例是( )A、x=1 B、x=-1 C、x=2 D、x=-24. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中( )A、有一个内角大于60° B、有一个内角小于60° C、每一个内角都大于60° D、每一个内角都小于60°5. 如图,若 ,则添加下列一个条件后,仍无法判定 的是( )
3. 下列选项中可以用来说明命题“若x2>1,则x>1”是假命题的反例是( )A、x=1 B、x=-1 C、x=2 D、x=-24. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中( )A、有一个内角大于60° B、有一个内角小于60° C、每一个内角都大于60° D、每一个内角都小于60°5. 如图,若 ,则添加下列一个条件后,仍无法判定 的是( )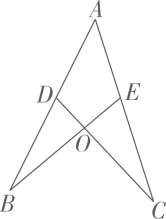 A、 B、 C、 D、6. 某大学生利用手机看球赛期间,把手机放在一个支架上面,如图,此手机能稳稳放在支架上利用的原理是( )
A、 B、 C、 D、6. 某大学生利用手机看球赛期间,把手机放在一个支架上面,如图,此手机能稳稳放在支架上利用的原理是( ) A、对称性 B、三角形的内角和为180° C、两点确定一条直线 D、三角形具有稳定性7. 在下列各题中,属于尺规作图的是( )A、用直尺画一工件边缘的垂线 B、用直尺和三角板画平行线 C、利用三角板画 的角 D、用圆规在已知直线上截取一条线段等于已知线段8. 已知、、是的三边,且满足 , 则的形状是( )A、等边三角形 B、等腰三角形 C、直角三角形 D、不能确定9. 如图,在中, , 点是边AB上的一个动点,则的度数可能是( )
A、对称性 B、三角形的内角和为180° C、两点确定一条直线 D、三角形具有稳定性7. 在下列各题中,属于尺规作图的是( )A、用直尺画一工件边缘的垂线 B、用直尺和三角板画平行线 C、利用三角板画 的角 D、用圆规在已知直线上截取一条线段等于已知线段8. 已知、、是的三边,且满足 , 则的形状是( )A、等边三角形 B、等腰三角形 C、直角三角形 D、不能确定9. 如图,在中, , 点是边AB上的一个动点,则的度数可能是( )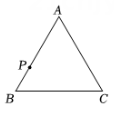 A、 B、 C、 D、
A、 B、 C、 D、二、填空题:本题共8小题,每小题3分,共24分
-
10. 请将命题"等腰三角形的底角相等"改写为"如果……,那么……"的形式:
.
11. 命题:面积相等的两个三角形是全等三角形是命题(填“真”或“假”)12. 等腰三角形的一个角等于 , 则它的顶角的度数是 .13. 如图,根据用直尺、圆规作一个角等于已知角的方法,画出了 . 则的理由是 .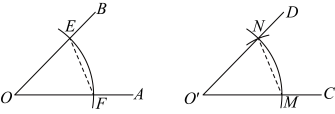 14. 如图,点C 是AE的中点,∠A=∠DCE,要使△ABC≌△CDE,则需要添加的条件可以是.(写出一个即可,不添加辅助线)
14. 如图,点C 是AE的中点,∠A=∠DCE,要使△ABC≌△CDE,则需要添加的条件可以是.(写出一个即可,不添加辅助线) 15. 如图,是等腰三角形屋架设计图的一部分,工人师傅在焊接立柱时,只需找到 BC 的中点就可以确定竖梁 AD 垂直横梁 BC,这种操作方法的依据是.
15. 如图,是等腰三角形屋架设计图的一部分,工人师傅在焊接立柱时,只需找到 BC 的中点就可以确定竖梁 AD 垂直横梁 BC,这种操作方法的依据是. 16. 如图,在中,边AC的垂直平分线交AC于点 , 交BC于点 , 若的周长为18,则BC的长为.
16. 如图,在中,边AC的垂直平分线交AC于点 , 交BC于点 , 若的周长为18,则BC的长为. 17. 如图,在△ABC中,AB=AC,∠ACB=60°,D 是线段BC上一点,连接AD,在线段AD上分别取两点E,F,连接CE,BF,若∠BAD=∠ACE,∠BFD=60°,CE=5,则AF的长为
17. 如图,在△ABC中,AB=AC,∠ACB=60°,D 是线段BC上一点,连接AD,在线段AD上分别取两点E,F,连接CE,BF,若∠BAD=∠ACE,∠BFD=60°,CE=5,则AF的长为
三、解答题:本题共8小题,共66分
-
18. 在△ABC中,AB=AC,∠A=36°.
(1)作∠ABC的平分线BD,交AC于点D(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)条件下,比较线段DA与BC的大小关系,请说明理由.
19. 如图,在中, , , 是边上的高,的平分线交于点 . 求的度数. 20. 如图,已知 , , 相交于点 , , .
20. 如图,已知 , , 相交于点 , , .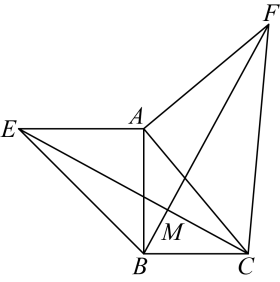 (1)、求证: .(2)、求证: .21. 如图,在 中,AD为中线,过点B作 于点E,过点C作 交AD的延长线于点 F.
(1)、求证: .(2)、求证: .21. 如图,在 中,AD为中线,过点B作 于点E,过点C作 交AD的延长线于点 F.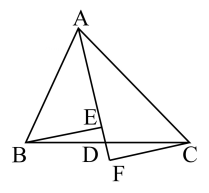 (1)、求证:BE=CF;(2)、若 的面积为7, 的面积为2,求 的面积.22. 如图,在中, , 是边上的中点,连接 , 平分交于点 , 过点作交于点 .
(1)、求证:BE=CF;(2)、若 的面积为7, 的面积为2,求 的面积.22. 如图,在中, , 是边上的中点,连接 , 平分交于点 , 过点作交于点 . (1)、若 , 求的度数;(2)、求证: .23. 如图,在中, , , AB的垂直平分线DE交AB于点D , 交BC于点E , 连接AE .
(1)、若 , 求的度数;(2)、求证: .23. 如图,在中, , , AB的垂直平分线DE交AB于点D , 交BC于点E , 连接AE . (1)、求证:AE是∠BAC的角平分线:(2)、若 , 求BC的长.24. 阅读下面材料:
(1)、求证:AE是∠BAC的角平分线:(2)、若 , 求BC的长.24. 阅读下面材料:小明遇到这样一个问题:如图1,在Rt△ABC中,∠ACB=90°,∠A=60°,CD平分∠ACB,试判断BC和AC、AD之间的数量关系.小明发现,在BC上截取CA′=CA,连接DA′,从而将问题解决(如图2).
 (1)、求证:△ADC≌△A′DC;(2)、试猜想写出BC和AC、AD之间的数量关系,并给出证明.25. 小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,表示小球静止时的位置,当小强用发声物体靠近小球时,小球从摆到位置,此时过点作于点 , 当小球摆到位置时,过点作于点 , 测得(图中的点在同一平面内).
(1)、求证:△ADC≌△A′DC;(2)、试猜想写出BC和AC、AD之间的数量关系,并给出证明.25. 小强在物理课上学习了发声物体的振动试验后,对其作了进一步的探究:在一个支架的横杆点处用一根细绳悬挂一个小球,小球可以自由摆动,如图,表示小球静止时的位置,当小强用发声物体靠近小球时,小球从摆到位置,此时过点作于点 , 当小球摆到位置时,过点作于点 , 测得(图中的点在同一平面内). (1)、猜想此时与的位置关系,并说明理由;(2)、求的长.
(1)、猜想此时与的位置关系,并说明理由;(2)、求的长.