第四章《三角形》提升卷—湘教版数学八(上)单元分层测
试卷更新日期:2025-10-05 类型:单元试卷
一、选择题:本题共10小题,每小题3分,共30分
-
1. 如图,在中, , , D是BC边上的一点,若的周长比的周长大2,则AD是( )
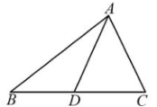 A、的高 B、的角平分线 C、的中线 D、都有可能2. 已知△ABC 的三边长分别为4,4,6,在△ABC 所在平面内画一条直线,将 分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( ).A、3条 B、4条 C、5条 D、6条3. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=34. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
A、的高 B、的角平分线 C、的中线 D、都有可能2. 已知△ABC 的三边长分别为4,4,6,在△ABC 所在平面内画一条直线,将 分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画( ).A、3条 B、4条 C、5条 D、6条3. 对于命题“若a2>b2 , 则a>b”,下面四组关于a,b的值中,能说明这个命题是假命题的是( )A、a=3,b=2 B、a=-3,b=2 C、a=3,b=-1 D、a=-1,b=34. 打碎的一块三角形玻璃如图所示,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( ) A、带①②去 B、带②③去 C、带③④去 D、带④去5. 如图,已知线段a , h作等腰△ABC , 使AB=AC , 且BC=a , BC边上的高AD=h . 张红的作法如下:
A、带①②去 B、带②③去 C、带③④去 D、带④去5. 如图,已知线段a , h作等腰△ABC , 使AB=AC , 且BC=a , BC边上的高AD=h . 张红的作法如下:
作线段BC=a;
作线段BC的垂直平分线MN , MN与BC相交于点D;
在直线MN上截取线段h;
连结AB , AC , 则△ABC为所求的等腰三角形.
上述作法的四个步骤中,有错误的一步你认为是( )
A、 B、 C、 D、6. 如图,已知在△ABC中,∠BAC=50°,∠ACB=54°,敏敏通过尺规作图得到AM,DN交于点O,连接OC,根据其作图痕迹,可得∠OCB 的度数为( ) A、25° B、27° C、29° D、31°7. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,与地面垂直,两脚在地面上用力一蹬,妈妈在距地面高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到的水平距离、分别为和 , . 爸爸在C处接住小丽时,小丽距离地面的高度是( )
A、25° B、27° C、29° D、31°7. 小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,与地面垂直,两脚在地面上用力一蹬,妈妈在距地面高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到的水平距离、分别为和 , . 爸爸在C处接住小丽时,小丽距离地面的高度是( )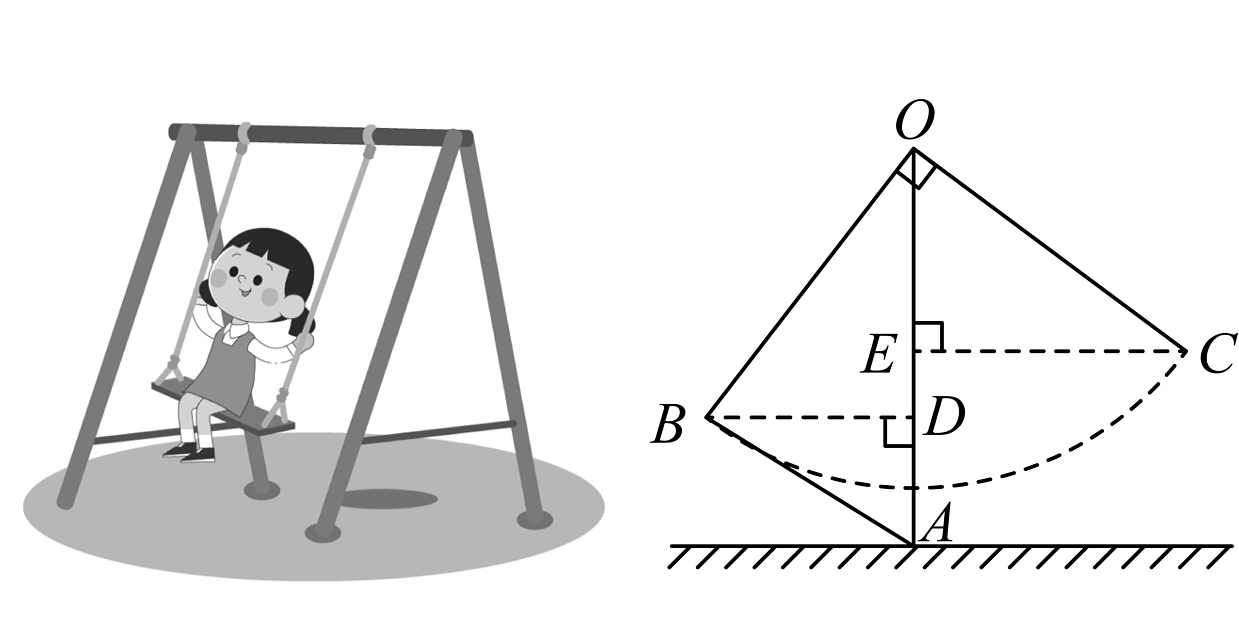 A、 B、 C、 D、8. 如图,在中, , 的平分线交于点D,过点D作交于点E,交于点F.若 , , , 则的周长是( )
A、 B、 C、 D、8. 如图,在中, , 的平分线交于点D,过点D作交于点E,交于点F.若 , , , 则的周长是( ) A、17 B、20 C、22 D、269. 如图,中, , 于 , 平分 , 于 , 与相交于点 , 是边的中点,连接与相交于点 , 下列结论:①;②;③是等腰三角形;④ .
A、17 B、20 C、22 D、269. 如图,中, , 于 , 平分 , 于 , 与相交于点 , 是边的中点,连接与相交于点 , 下列结论:①;②;③是等腰三角形;④ .正确的是( ).
 A、①②③ B、①②④ C、③④ D、①②③④
A、①②③ B、①②④ C、③④ D、①②③④二、填空题:本题共8小题,每小题3分,共24分
-
10. 命题“等边三角形的每个内角都等于60°”的逆命题是命题.(填“真”或“假”)11. 三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数等于 .
 12. 如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画个三角形.
12. 如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画个三角形. 13. 一个零件的形状如图,按规定∠A=90°,∠B=∠D=25°,判断这个零件是否合格,只要检验∠BCD的度数就可以了.量得∠BCD=140°,这个零件(填“合格”或“不合格”).
13. 一个零件的形状如图,按规定∠A=90°,∠B=∠D=25°,判断这个零件是否合格,只要检验∠BCD的度数就可以了.量得∠BCD=140°,这个零件(填“合格”或“不合格”).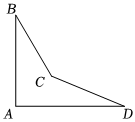 14. 已知 的周长为 ,当 的值为时, 是等腰三角形.15. 小明同学将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件是 .
14. 已知 的周长为 ,当 的值为时, 是等腰三角形.15. 小明同学将几种三角形的关系整理如图,请帮他在括号内填上一个适当的条件是 . 16. 如图,∠A=52°,O是AB,AC的垂直平分线的交点,则∠OCB= .
16. 如图,∠A=52°,O是AB,AC的垂直平分线的交点,则∠OCB= .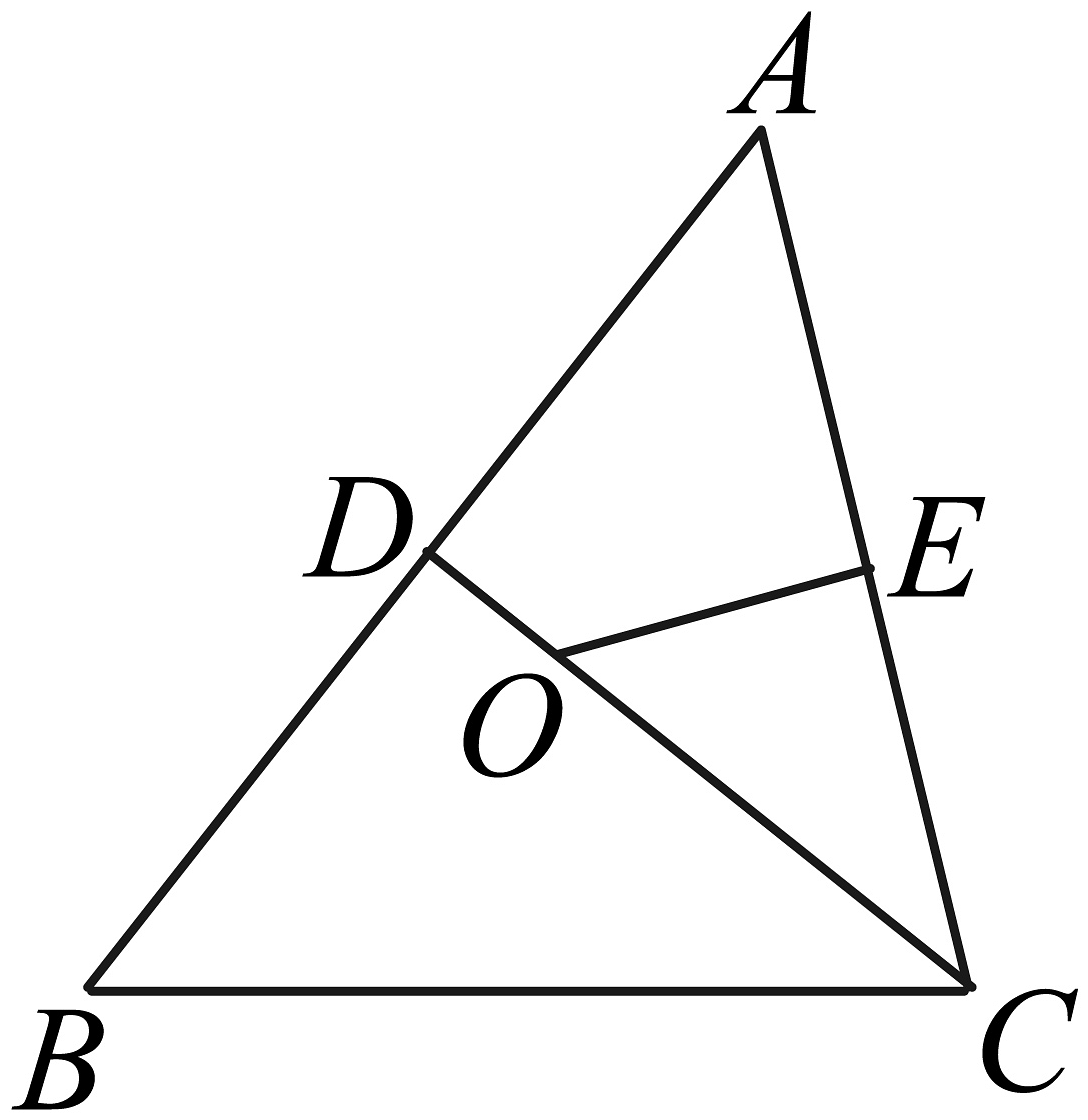 17. 如图是折叠式沙发椅的示意图,若将度数调到图上所示度数为最舒适角度,求此时 .
17. 如图是折叠式沙发椅的示意图,若将度数调到图上所示度数为最舒适角度,求此时 .
三、解答题:本题共8小题,共66分
-
18. 如图,为等边三角形,在内作射线 , 点B关于射线的对称点为点D,连接 , 作射线交于点E,连接 .
 (1)、依题意补全图形;(2)、设 , 求的大小(用含的代数式表示);(3)、用等式表示 , , 之间的数量关系,并证明.19. 如图,在中, , .
(1)、依题意补全图形;(2)、设 , 求的大小(用含的代数式表示);(3)、用等式表示 , , 之间的数量关系,并证明.19. 如图,在中, , .
①分别以点A、B为圆心,以大于的长度为半径作弧,分别交于两点,连接这两点的直线与交于点D,与交于点F,连结;
②以点A为圆心,任意长为半径作弧,分别与、交于两点,再以这两点为圆心,以大于这两点间距离的一半的长度为半径作弧,两弧交于一点,连结点A与这一点交于点E.
(1)、通过以上作图,可以发现直线是 , 射线是;(在横线上填上合适的选项)A.线段的垂直平分线 B.的角平分线
C.的中线 D.的角平分线
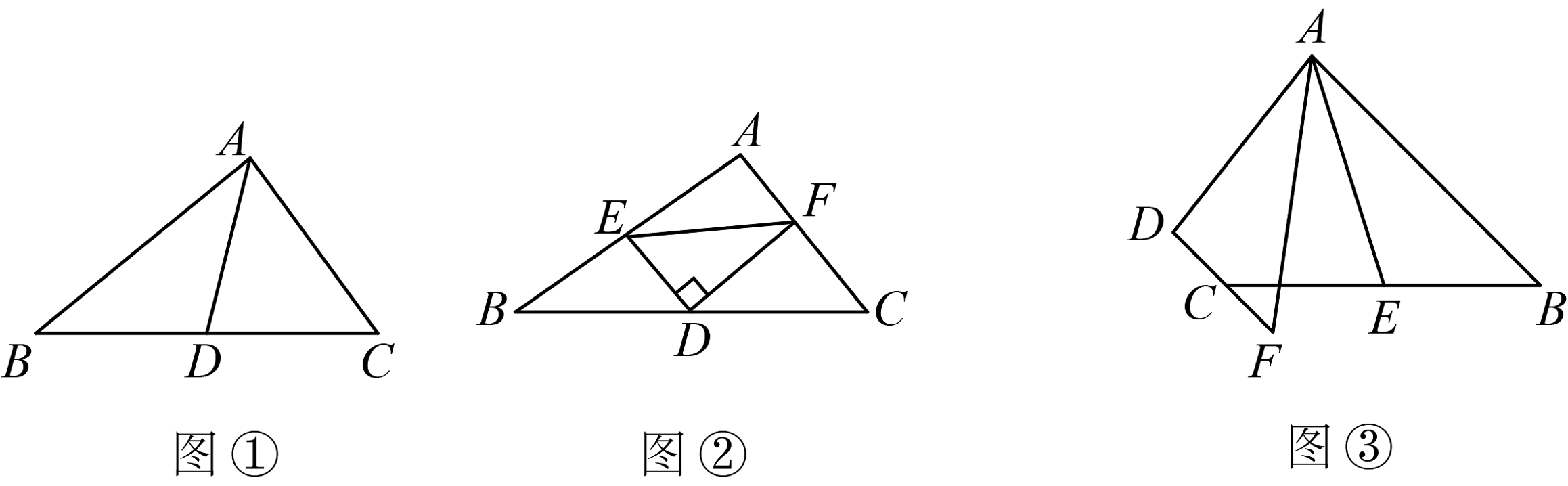
(2)、在(1)所作的图中,求的度数.20. (1)如图①,在中,若 , , 为边上的中线,求的取值范围;(2)如图②,在中,点D是的中点, , 交于点E,交于点F,连接 , 判断与的大小关系并证明;
(3)如图③,在四边形中, , 与的延长线交于点F,点E是的中点,若是的角平分线.试探究线段 , , 之间的数量关系,并加以证明.
 21. 阅读下面材料:
21. 阅读下面材料:小明遇到这样一个问题:
如图9-①,在△ABC中,AD平分∠BAC,∠ABC=2∠C,求证:AC=AB+BD;
小明通过思考发现,可以通过“截长、补短”两种方法解决问题:
方法一:如图9-②,在AC上截取AE,使得AE=AB,连接DE,可以得到全等三角形,进而解决问题;
方法二:如图9-③,延长AB到点E,使得BE=BD,连接DE,可以得到等腰三角形,进而解决问题.
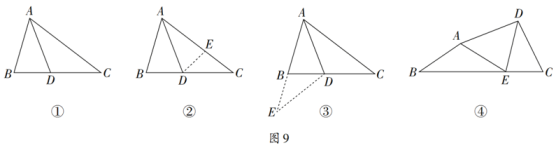 (1)、根据以上材料,任选一种方法证明:AC=AB+BD;(2)、如图9-④,四边形ABCD中,E是BC上一点,EA=ED,
(1)、根据以上材料,任选一种方法证明:AC=AB+BD;(2)、如图9-④,四边形ABCD中,E是BC上一点,EA=ED,∠C=2∠B,∠DAE+∠B=90°,探究DC,CE,BE之间的数量关系,并证明.
22. 如图①,用一根细绳从质地均匀的三角形薄板的重心处穿过,并将其悬挂在支架上,观察发现三角形薄板正好保持水平,数学兴趣小组对产生这一现象的原因进行了探究.请你帮助他们完成下列问题: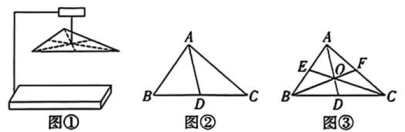 (1)、如图②,小组成员在三角形薄板ABC 上画出中线AD,可以得到 (填“>”“=”或“<”);(2)、如图③,三角形薄板ABC的三条中线AD,CE,BF相交于点O,试判断三角形薄板ABC 被三条中线所分成的六个小三角形的面积之间的数量关系,并说明理由;(3)、结合(2)中的结论,试猜想AO:OD,BO:OF,CO:OE 的值,并说明理由.23. 在四边形中, , , , E为中点,连接 , 交于点F.
(1)、如图②,小组成员在三角形薄板ABC 上画出中线AD,可以得到 (填“>”“=”或“<”);(2)、如图③,三角形薄板ABC的三条中线AD,CE,BF相交于点O,试判断三角形薄板ABC 被三条中线所分成的六个小三角形的面积之间的数量关系,并说明理由;(3)、结合(2)中的结论,试猜想AO:OD,BO:OF,CO:OE 的值,并说明理由.23. 在四边形中, , , , E为中点,连接 , 交于点F. (1)、当时,______,_____;(2)、当的大小改变时,的度数是否发生改变?若变化,求的变化范围,若不变,求的度数;(3)、猜想之间的数量关系,并说明理由;(4)、若 , 则_______.24. 数学模型可以用来解决一类问题,是数学应用的基本途径,通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地.
(1)、当时,______,_____;(2)、当的大小改变时,的度数是否发生改变?若变化,求的变化范围,若不变,求的度数;(3)、猜想之间的数量关系,并说明理由;(4)、若 , 则_______.24. 数学模型可以用来解决一类问题,是数学应用的基本途径,通过探究图形的变化规律,再结合其他数学知识的内在联系,最终可以获得宝贵的数学经验,并将其运用到更广阔的数学天地. (1)、发现问题:如图1,在和中, , , , 连接 , 延长交于点D.则与的数量关系: , ;(2)、类比探究:如图2,在和中, , , , 连接 , 延长交于点D.请猜想与的数量关系及的度数,并说明理由;(3)、拓展延伸:如图3,和均为等腰直角三角形, , 连接 , 且点B,E,F在一条直线上,过点A作 , 垂足为点M.请猜想之间的数量关系并说明理由.
(1)、发现问题:如图1,在和中, , , , 连接 , 延长交于点D.则与的数量关系: , ;(2)、类比探究:如图2,在和中, , , , 连接 , 延长交于点D.请猜想与的数量关系及的度数,并说明理由;(3)、拓展延伸:如图3,和均为等腰直角三角形, , 连接 , 且点B,E,F在一条直线上,过点A作 , 垂足为点M.请猜想之间的数量关系并说明理由.