人教版九(上) 第二十三章 旋转 单元测试培优卷
试卷更新日期:2025-10-05 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 如图,将绕B点顺时针方向旋转一个角α到 , 点A的对应点D恰好落在上,且 . 若 , 则α的度数为( )
 A、30° B、40° C、45° D、36°2. 如图,四边形是正方形,将绕点顺时针旋转得 , 连接 , 则的角度为( )
A、30° B、40° C、45° D、36°2. 如图,四边形是正方形,将绕点顺时针旋转得 , 连接 , 则的角度为( )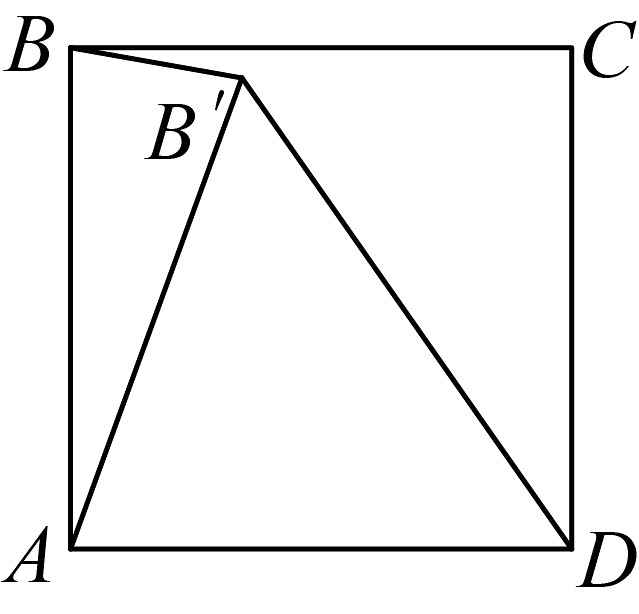 A、 B、 C、 D、3. 如图,把绕着点顺时针方向旋转 , 得到△ , 点刚好落在边上.则
A、 B、 C、 D、3. 如图,把绕着点顺时针方向旋转 , 得到△ , 点刚好落在边上.则 A、 B、 C、 D、4. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是
A、 B、 C、 D、4. 如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是 A、55° B、60° C、65° D、70°5. 如图,将绕顶点C逆时针旋转角度α得到 , 且点B刚好落在上.若 , , 则α等于( )
A、55° B、60° C、65° D、70°5. 如图,将绕顶点C逆时针旋转角度α得到 , 且点B刚好落在上.若 , , 则α等于( ) A、 B、 C、 D、6. 如图,绕点逆时针旋转得到 , 点恰好落在上,则的度数为( )
A、 B、 C、 D、6. 如图,绕点逆时针旋转得到 , 点恰好落在上,则的度数为( ) A、 B、 C、 D、7. 如图,菱形的对角线交于原点O, , . 将菱形绕原点O逆时针旋转,每次旋转 , 则第2023次旋转结束时,点C的坐标为( )
A、 B、 C、 D、7. 如图,菱形的对角线交于原点O, , . 将菱形绕原点O逆时针旋转,每次旋转 , 则第2023次旋转结束时,点C的坐标为( ) A、 B、 C、 D、8. 如图,边长为8的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC将线段EC绕点C逆时针旋转60°得到FC , 连接DF , 则在点E运动过程中,DF的最小值是( )
A、 B、 C、 D、8. 如图,边长为8的等边三角形ABC中,E是对称轴AD上的一个动点,连接EC将线段EC绕点C逆时针旋转60°得到FC , 连接DF , 则在点E运动过程中,DF的最小值是( ) A、4 B、3 C、2 D、19. 如图,是正内一点, , , , 将线段BO以点为旋转中心逆时针旋转得到线段 , 下列结论,①可以由绕点逆时针旋转得到;②点与的距离为5;③;④四边形面积;⑤ , 其中正确的结论是( )
A、4 B、3 C、2 D、19. 如图,是正内一点, , , , 将线段BO以点为旋转中心逆时针旋转得到线段 , 下列结论,①可以由绕点逆时针旋转得到;②点与的距离为5;③;④四边形面积;⑤ , 其中正确的结论是( ) A、①④⑤ B、①③④ C、①③④⑤ D、①③⑤
A、①④⑤ B、①③④ C、①③④⑤ D、①③⑤二、填空题:本大题共5小题,每小题3分,共15分.
-
10. 如图,在四边形ABCD中,∠BAD=45°,∠BCD=90°,连接BD、CA , 若CA平分∠BCD , , BC=5,则BD= .
 11. 如图,将绕点顺时针旋转得到 , 点的对应点落在的延长线上,连接 , 若 , , , 则的长为 .
11. 如图,将绕点顺时针旋转得到 , 点的对应点落在的延长线上,连接 , 若 , , , 则的长为 . 12. 如图,在中, , 将绕点逆时针旋转,得到 , 点恰好落在的延长线上,则旋转角的度数是 .
12. 如图,在中, , 将绕点逆时针旋转,得到 , 点恰好落在的延长线上,则旋转角的度数是 . 13. 如图,在平直角坐标系中,点A的坐标为 , 点的坐标为 . 以 , 为边作矩形 , 若将矩形绕点逆时针旋转 , 得到矩形 , 则点的坐标为 .
13. 如图,在平直角坐标系中,点A的坐标为 , 点的坐标为 . 以 , 为边作矩形 , 若将矩形绕点逆时针旋转 , 得到矩形 , 则点的坐标为 .
三、解答题:本大题共8小题,共75分.
-
14. 四边形是正方形,旋转一定角度后得到 , 如图所示,如果 , .
 (1)、旋转中心是________,旋转角度是________;(2)、的长度是________;(3)、与的位置关系是________,与的数量关系是________.15. 如图,已知的三个顶点的坐标分别为 , , .
(1)、旋转中心是________,旋转角度是________;(2)、的长度是________;(3)、与的位置关系是________,与的数量关系是________.15. 如图,已知的三个顶点的坐标分别为 , , . (1)、画出关于原点成中心对称的图形;(2)、是的边上一点,将平移后点的对称点 , 请画出平移后的;(3)、若和关于某一点成中心对称,则对称中心的坐标为 .16. 如图,等腰直角中, , 点在上,将绕顶点沿顺时针方向旋转后得到.
(1)、画出关于原点成中心对称的图形;(2)、是的边上一点,将平移后点的对称点 , 请画出平移后的;(3)、若和关于某一点成中心对称,则对称中心的坐标为 .16. 如图,等腰直角中, , 点在上,将绕顶点沿顺时针方向旋转后得到. (1)、求的度数;(2)、若 , , 求的长.17. 如图,在中, , 将绕点A顺时针旋转得到使点C的对应点E落在上,连接 .
(1)、求的度数;(2)、若 , , 求的长.17. 如图,在中, , 将绕点A顺时针旋转得到使点C的对应点E落在上,连接 . (1)、若 , 求的度数;(2)、若 , 求的长.18. 如图,的顶点坐标分别为 , , .
(1)、若 , 求的度数;(2)、若 , 求的长.18. 如图,的顶点坐标分别为 , , . (1)、画出绕点A逆时针旋转后得到的;(2)、画出关于原点O的对称图形 .(3)、P为x轴上一点,且取得最小值,直接写出点P的坐标为________.19. 如图,中, , 将绕点A逆时针旋转得到 , 与交于点D , 与交于点E , 与交于点F , 当B、D、F重合时停止旋转.
(1)、画出绕点A逆时针旋转后得到的;(2)、画出关于原点O的对称图形 .(3)、P为x轴上一点,且取得最小值,直接写出点P的坐标为________.19. 如图,中, , 将绕点A逆时针旋转得到 , 与交于点D , 与交于点E , 与交于点F , 当B、D、F重合时停止旋转. (1)、证明:在旋转过程中;(2)、如图1,当平分时,证明:;(3)、如图2,若 , , 在旋转过程中,当是等腰三角形时,求该等腰三角形底边的长度.20. 综合与实践
(1)、证明:在旋转过程中;(2)、如图1,当平分时,证明:;(3)、如图2,若 , , 在旋转过程中,当是等腰三角形时,求该等腰三角形底边的长度.20. 综合与实践【问题情境】
我们定义:如图(a),在中,把AB绕点A顺时针旋转得到 , 把AC绕点A逆时针旋转得到 , 连接 . 当时,我们称是的“旋补三角形”,的边上的中线AD叫做的“旋补中线”,点A叫做“旋补中心”.

(a) (b) (c) (d)
(1)、【特例感知】在图(b)和图(c)中,是的“旋补三角形”,AD是的“旋补中线”.①如图(b),当为等边三角形时,AD与BC的数量关系为BC;
②如图(c),当 , 时,则AD长为 .
(2)、【猜想论证】如图(a),当为任意三角形时,猜想AD与BC的数量关系,并给予证明.(3)、【拓展应用】如图(d),在四边形ABCD中, , , , , . 在四边形内部是否存在点P , 使是的“旋补三角形”?若存在,给予证明,并求出的“旋补中线”长;若不存在,说明理由.