人教版七（上）第三章代数式单元测试基础卷

试卷更新日期：2025-10-05 类型：单元试卷

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 下列各式中，符合代数式书写规则的是（）

A、 $- 2 \frac{1}{6} p$ B、 $\frac{7}{3} x^{2}$ C、 $a \times \frac{1}{4}$ D、 $2 y \div x$

查看试题解析
2. 用代数式表示： “ $a$ 的相反数与 $b$ 的 3 倍的差”，结果正确的是（）

A、 $- a - 3 b$ B、 $- a + 3 b$ C、 $- (a - 3 b)$ D、 $3 (- a - b)$

查看试题解析
3. 四四跟同学在某餐厅吃饭，如图为此餐厅的菜单，若他们所点的餐点总共为16份意大利面，x杯饮料，y个蛋挞，则他们点了几份A餐
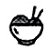
A餐：一份意大利面
B餐：一份意大利面加一杯饮料
C餐：一份意大利面加一杯饮料与两个蛋挞

A、16-x B、16-x- $\frac{y}{2}$ C、16- $\frac{y}{2}$ D、16-x+ $\frac{y}{2}$

查看试题解析
4. 当 $x = 2$ 时，整式 $m x^{3} - n x + 3 = 2023$ ，则当 $x = - 2$ 时，整式 $m x^{3} - n x + 3$ 的值为（）

A、2022 B、2019 C、 $- 2016$ D、 $- 2017$

查看试题解析
5. 已知代数式 $k^{2} x + k$ ，当 $x$ 取一个值时，代数式 $k^{2} x + k$ 对应的值如下表所示：则下列代数式的值最大的是（　　）
$x$
$- 2$
$- 1$
0
1
2
$k^{2} x + k$
0
0.25
0.5
0.75
1

A、 $- 4 k^{2} + 2 k$ B、 $- 2 k^{2} + 2 k$ C、2 $k^{2} + 2 k$ D、4 $k^{2} + 2 k$

查看试题解析
6. 已知整数a，b，c，d 满足 abcd=25，且a>b>c>d，那么|a+b|+|c+d|等于（）.

A、0 B、10 C、2 D、12

查看试题解析
7. 将长方形 A 和长方形 B 按如图所示摆放，由图中信息可知，“？”的值为（）

A、6.75 B、6.5 C、6.25 D、6

查看试题解析
8. 数学家欧拉最早用记号 $f (x)$ 表示关于 $x$ 的多项式，用 $f (a)$ 表示 $x$ 等于某数 $a$ 时的多项式的值．例如：多项式 $f (x) = x^{2} - x + 1$ ，当 $x = 4$ 时，多项式的值 $f (4) = 4^{2} - 4 + 1 = 13$ ．已知多项式 $f (x) = m x^{3} - n x + 1$ ，当 $x = 1$ 时，多项式的值 $f (1) = 14$ ，则 $f (- 1)$ 的值为（　　）

A、 $- 14$ B、 $- 12$ C、 $- 13$ D、13

查看试题解析
9. 若 $|m| = 2$ ， $|n| = 3$ ，且 $| m ＋ n | ＝ m ＋ n$ ，则 $\frac{n}{m} =$ （）

A、 $\frac{3}{2}$ B、 $- \frac{3}{2}$ C、 $\frac{3}{2}$ 或 $- \frac{3}{2}$ D、 $\frac{2}{3}$ 或 $- \frac{2}{3}$

查看试题解析
10. 大约从 20 世纪 50 年代开始，许多国家流传着这样一个数学猜想，其原理如下图数值转换器。若开始输入 $x$ 的值是 5 ，则第 1 次输出的结果是 16 ，第 2 次输出的结果是 8 ，第 3 次输出的结果是 4 ．依次继续下去，第 2025 次输出的结果是（）

A、1
B、2
C、3 D、4

查看试题解析

二、填空题：本大题共5小题，每小题3分，共15分.

11. 用代数式表示“ $x$ 的平方与 $y$ 的平方的差”是．

查看试题解析
12. 如图是一面墙与篱笆围成的长方形园子，园子的宽为a米，篱笆的总长度为b米，门的宽度为1米，则园子的长是米（用含a，b的代数式表示）．

查看试题解析
13. 如图，一个手工串珠作品由5颗红色珠子与5颗黑色珠子串成，红色珠子每颗m 元，购买这些珠子共花费30元，则黑色珠子每颗元．

查看试题解析
14. 若 $x^{3} + 3 x$ 的值为9，则 $x^{3} + 3 x - 2$ 的值为．

查看试题解析
15. 当输入 $a = - 2$ ， $b = - 3$ 时，输出的 $y$ 的值为．

查看试题解析

三、解答题：本大题共8小题，共75分.

16. 请根据图示的对话解答下列问题．求：

(1)、a，b，c的值；

(2)、 $8 - a + b - c$ 的值．

查看试题解析
17. 某商场销售一种西装和领带，西装每套定价1000元，领带每条定价200元．商场决定活动期间向客户提供两种优惠方案．
方案一：买一套西装送一条领带；
方案二：西装和领带都按定价的 $90 %$ 付款．现某客户要到该商场购买西装20套，领带x条(x>20)．

(1)、若该客户按方案一购买，需付款　　　元．(用含x的代数式表示)
若该客户按方案二购买，需付款　　　元．(用含x的代数式表示)

(2)、请结合问题的背景，说明代数式 $20 x - 2000$ 的意义；

(3)、若 $x = 30$ ，通过计算说明此时按哪种方案购买较为合算?

(4)、当 $x = 30$ 时，你能给出一种更为省钱的购买方案吗?试写出你的购买方法．

查看试题解析
18. 某校决定采购一批某品牌的足球和跳绳，经市场调查发现，足球每个定价 $120$ 元，跳绳每根定价 $20$ 元．现有 $A, B$ 两家商店提出了各自的优惠方案． $A$ 商店：买一个足球送一根跳绳； $B$ 商店：足球和跳绳都按定价的 $90 %$ 销售，已知学校要采购足球 $100$ 个，跳绳 $x$ 根 $(x > 100)$ ．

(1)、若在 $A$ 商店购买，需付款______元（用含 $x$ 的代数式表示，并化简）；若在 $B$ 商店购买，需付款______元（用含 $x$ 的代数式表示，并化简）．

(2)、若 $x = 300$ ，通过计算说明此时在哪家商店购买较为划算？

查看试题解析
19. 如图，正方形 $A B C D$ 的边长为a．

(1)、根据图中数据，用含a的代数式表示阴影部分的面积；

(2)、当 $a = 6$ 时，求阴影部分的面积．

查看试题解析
20. 如图，正方形 $A B C D$ 的边长为x．

(1)、根据图中数据，用含x，y的代数式表示阴影部分的面积S；

(2)、当 $x = 7$ ， $y = 3$ 时，求阴影部分的面积．

查看试题解析
21. 已知小刚家上半年的用电情况如表（以200度为标准，超出200度记为正、低于200度记为负）：
一月份
二月份
三月份
四月份
五月份
六月份
$- 50$
$+ 30$
$- 26$
$- 45$
$+ 36$
$+ 25$
请解决以下问题：

(1)、小刚家用电量最多的是月份，实际用电量为度；
为响应国家节能减排的号召，鼓励人们节约用电，保护能源，某市实施用电“阶梯价格”收费制度．收费标准如表：
居民每月用电量
单价（元/度）
不超过50度的部分
0.5
超过50度但不超过200度的部分
0.6
超过200度的部分
0.8

(2)、小刚家一月份应交纳电费元；

(3)、若小刚家七月份用电量为x度，求小刚家七月份应交纳的电费（用含x的代数式表示）．

查看试题解析
22. 在学习一个数的绝对值过程中，化简 $|a|$ 时，可以这样分类：当 $a > 0$ 时， $|a| = a$ ；当， $a = 0$ 时， $|a| = 0$ ；当 $a < 0$ 时， $|a| = - a$ ，请用这种方法解决下列问题：

(1)、当 $a = 3$ 时， $\frac{a}{|a|} =$ ______，当 $a = - 2$ 时， $\frac{a}{|a|} =$ ______．

(2)、已知a，b是有理数，当 $a < 0$ ， $b > 0$ 时，求 $\frac{a}{|a|} + \frac{b}{|b|}$ 的值．

(3)、已知 $|a| = 4, |b| = 7$ ，且 $a < b$ ，求 $a + b$ 的值．

查看试题解析
23. 用三角形和六边形按如图所示的规律拼图案.

(1)、第5个图案中，三角形有个，六边形有个.

(2)、第 $n (n$ 为正整数 $)$ 个图案中，三角形与六边形各有多少个？

(3)、是否存在某个符合上述规律的图案，其中有100个三角形和40个六边形？如果存在，指出是第几个图案；如果不存在，请说明理由.

查看试题解析

一月份	二月份	三月份	四月份	五月份	六月份
$- 50$	$+ 30$	$- 26$	$- 45$	$+ 36$	$+ 25$

居民每月用电量	单价（元/度）
不超过50度的部分	0.5
超过50度但不超过200度的部分	0.6
超过200度的部分	0.8

$x$	$- 2$	$- 1$	0	1	2
$k^{2} x + k$	0	0.25	0.5	0.75	1

人教版七（上） 第三章 代数式 单元测试基础卷

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的。

二、填空题：本大题共5小题，每小题3分，共15分.

三、解答题：本大题共8小题，共75分.

人教版七（上）第三章代数式单元测试基础卷