-
1、
 (1)、如图,△ABC中,DE∥BC,CD⊥AB,GF⊥AB,试说明∠CDE=∠BGF;(2)、若把(1)中的已知“GF⊥AB”与结论“∠CDE=∠BGF”对调,所得的命题是真命题还是假命题?请判断并说明理由.
(1)、如图,△ABC中,DE∥BC,CD⊥AB,GF⊥AB,试说明∠CDE=∠BGF;(2)、若把(1)中的已知“GF⊥AB”与结论“∠CDE=∠BGF”对调,所得的命题是真命题还是假命题?请判断并说明理由. -
2、小豪发现一个命题:“如果两个无理数a,b满足a+b≠0,那么这两个无理数的和是无理数”.这个命题是命题(填“真”或“假”),请举例说明:.
-
3、下列命题中,是假命题的是( )A、平方根等于它本身的数是0 B、对于任何实数x,有 C、三角形三个内角的和等于180° D、三角形的两边之和大于第三边
-
4、如图,在 Rt△ABC中,∠ACB=90°,D 为AB 中点,点 E 在 BC 边上(点E 不与点 B,C重合),连接DE,过点 D 作DF⊥DE交AC 于点F,连接EF.
 (1)、试说明:(2)、若AC=7,BC=5,EC=1,直接写出AF的长.
(1)、试说明:(2)、若AC=7,BC=5,EC=1,直接写出AF的长. -
5、探究:
 (1)、图(1)是由四个全等的直角三角形紧密拼接形成的飞镖状图形,若AB+AC=20,OC=5,求该飞镖状图形的面积.(2)、图(2)是由八个全等的直角三角形紧密拼接形成的大正方形ABCD,记图中正方形ABCD,正方形EFGH,正方形MNKT 的面积分别为 S1 , S2 , S3.若 求 的值.
(1)、图(1)是由四个全等的直角三角形紧密拼接形成的飞镖状图形,若AB+AC=20,OC=5,求该飞镖状图形的面积.(2)、图(2)是由八个全等的直角三角形紧密拼接形成的大正方形ABCD,记图中正方形ABCD,正方形EFGH,正方形MNKT 的面积分别为 S1 , S2 , S3.若 求 的值. -
6、如图,在△ABC 中,∠ACB=90°,AC=12,BC=9,射线CD 与边AB 交于点 D. E,F分别为AD,BD的中点,设点E,F到射线CD的距离分别为m,n,则m+n的最大值为

-
7、成都质检,中]如图,在△ABC 中,∠ACB=90°,AC=3,BC=4,点 D 在边 AB 上,AD=AC,AE⊥CD,交 BC,CD 于点E,F,则BE的长是.

-
8、如图,点 A 是射线 BM 外一点,连接 AB,若 AB =5cm ,点A 到BM 的距离为3cm,动点 P 从点 B出发沿射线 BM 以2cm /s的速度运动.设运动的时间为 t s,当△ABP 为直角三角形时,t 的值为 ( )
 A、 B、2 C、2或 D、2或
A、 B、2 C、2或 D、2或 -
9、如图,在Rt△ABC 中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为S1 , S2 , S3 , 若 则图中阴影部分的面积为( )
 A、6 B、12 C、10 D、8
A、6 B、12 C、10 D、8 -
10、如图,点P 为Rt△ABC的边BC上一点,已知 PC=5,AC=10,折线 P-B-A 与折线 P-C-A 的长度相等,则边 BC 的长为( )
 A、6.5 B、7 C、7.5 D、8
A、6.5 B、7 C、7.5 D、8 -
11、已知一个直角三角形的两条边长分别为3 和5,则第三条边长的平方为.
-
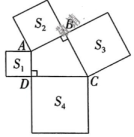
12、如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形 ABCD的四条边为边长,向外作四个正方形,面积分别为S1 , S2 , S3 , S4 , 若 则
-
13、如图,在△ABC 中,AB=AC=5,BC=6,则AC边上的高BD的长为( )
 A、4 B、4.4 C、4.8 D、5
A、4 B、4.4 C、4.8 D、5 -
14、如图,在Rt△ABC 中,∠ACB=90°,△ABC 的面积为24cm2 , 在AB 同侧分别以AB,BC,AC 为直径作三个半圆,则阴影部分的面积为cm2.

-
15、如图,AD 是△ABC 的高,分别以AB,BD,DC,CA 为边向外作正方形,其中3个正方形的面积如图所示,则第四个正方形的面积为 ( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
16、如图,在△ABC中,CD⊥AB 于点 D,E 在 AD 上,连接 CE,AE=CE.若AD=6,BC=5,BD=3,则DE的长为.

-
17、如图,Rt△ABC的顶点A,B 都在由边长为1 的小正方形组成的方格纸的格点上,且∠C=90°,则AB的长为.

-
18、如图,直线 AB⊥CD,垂足为 O,AO=15,CO=8,以点A 为圆心,AC 的长为半径画弧,交直线AB 于点 E,则OE 的长为( )
 A、8 B、6 C、4 D、2
A、8 B、6 C、4 D、2 -
19、在△ABC中,若∠ABC=90°,则下列正确的是 ( )A、BC=AB+AC B、 C、 D、
-
20、一辆装满货物的卡车,高2.5cm,宽1.6m,要开进上边是半圆,下边是长方形的隧道,如图所示,已知半圆的直径为2m,长方形的另一条边长是2.3m .
 (1)、此卡车是否能通过隧道?试说明你的理由.(2)、为了适应车流量的增加,现把隧道改为双行道,要使宽为1.2m,高为2.8 m的卡车能安全通过,那么此隧道的宽至少增加到多少?
(1)、此卡车是否能通过隧道?试说明你的理由.(2)、为了适应车流量的增加,现把隧道改为双行道,要使宽为1.2m,高为2.8 m的卡车能安全通过,那么此隧道的宽至少增加到多少?