相关试卷

1、若二次根式 $\frac{\sqrt{x - 2024}}{x}$ 在实数范围内有意义，则 $x$ 的取值范围是（）

A、 $x > 2024$ B、 $x \geq 2024$ C、 $x < 2024$ D、 $x \leq 2024$

查看解析
2、下列各数中，为无理数的是（）

A、 $\frac{1}{3}$ B、 $2.5$ C、 $0$ D、 $π$

查看解析
3、如图，等边 $△ A B C$ 的边长为4， $A D$ 是 $B C$ 边上的中线， $F$ 是 $A D$ 边上的动点， $E$ 是 $A C$ 边上一点，若 $A E = 2$ ，当 $E F + C F$ 取得最小值时，则 $∠ E C F =$ ．

查看解析
4、已知关于x的一元二次方程 $(a + b) x^{2} + 2 c x + (b - a) = 0$ ，其中 $a$ 、 $b$ 、 $c$ 分别为 $△ A B C$ 三边的长．

(1)、如果 $x = - 1$ 是方程的根，试判断 $△ A B C$ 的形状，并说明理由；

(2)、如果方程有两个相等的实数根，试判断 $△ A B C$ 的形状，并说明理由；

(3)、如果 $△ A B C$ 是等边三角形，试求这个一元二次方程的根．

查看解析
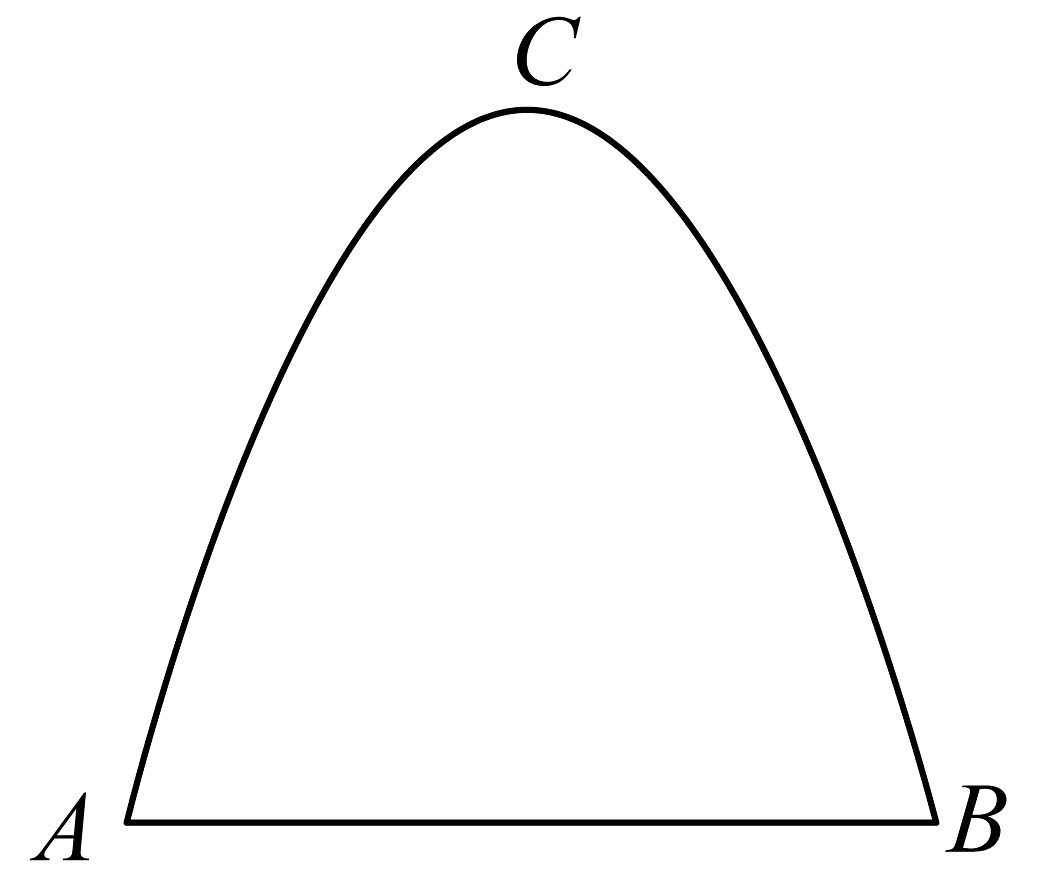
5、某工厂大门是抛物线形水泥建筑，大门地面宽AB为4m，顶部C距离地面的高度为4.4m，现有一辆货车，其装货宽度为2.4m，高度2.8米，请通过计算说明该货车能否通过此大门？

查看解析
6、抛物线 $y = a x^{2} + b x + c$ 上部分点的横坐标 $x$ ，纵坐标 $y$ 的对应值如下表：
x
…
-2
-1
0
1
2
…
y
…
0
-4
-4
0
8
…
（1）试确定该抛物线的对称轴及当 $x = - 3$ 时对应的函数值；
（2）试确定抛物线 $y = a x^{2} + b x + c$ 的解析式．

查看解析
7、西安大唐不夜城在2020年五一假期，接待游客达20万人次，在2022年五一假期，接待游客达28.8万人次．一家特色小面店希望在五一长期限期间获得好的收益，经测算知，该小面成本价为每碗6元，借鉴经验：若每碗卖25元，平均每天将销售300碗，若价格每降低1元，则平均每天多销售30碗.

(1)、求出2020至2022年五一长假期间游客人次的年平均增长率.

(2)、为了更好地维护西安城市形象，店家规定每碗售价不得超过20元，则当每碗售价定为多少元时，店家才能实现每天利润6300元？

查看解析
8、如图， $△ A B C$ 绕着顶点 $A$ 逆时针旋转到 $△ A D E$ ， $∠ B = 40 °$ ， $∠ E = 60 °$ ， $A B ∥ D E$ ，求 $∠ D A C$ 的度数．

查看解析
9、解方程：

(1)、 $x^{2} - 6 x + 3 = 0$

(2)、 $3 x (x - 2) = 2 (x - 2)$

查看解析
10、如图，抛物线y＝x²+5x+4与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接AC，点P在线段AC上，过点P作x轴的垂线交抛物线于点Q，则线段PQ长的最大值为．

查看解析
11、二次函数 $y = 4 {(x - 1)}^{2} + 1$ 的图象的顶点坐标是．

查看解析
12、点 $A (a - 1, - 5)$ 与点 $B (- 3, 1 - b)$ 关于原点对称，则 ${(a + b)}^{2024}$ 的值为．

查看解析
13、从某幢建筑物2.25米高处的窗口A用水管向外喷水，水流呈抛物线，如果抛物线的最高点M离墙1米，离地面3米，那么水流落点B与墙的距离OB是（）

A、1米 B、2米 C、3米 D、4米

查看解析
14、若点 $P (- a, a - 3)$ 关于原点对称的点是第二象限内的点，则 $a$ 满足（）

A、 $a > 3$ B、 $0 < a \leq 3$ C、 $a < 0$ D、 $a < 0$ 或 $a > 3$

查看解析
15、某景点的门票价格为220元，日接待游客5000人．当门票价格每提高10元，日游客数减少50人.若想每天的门票收入达到138万元，问门票价格需提高多少元？设门票价格提高x元，则可列方程为（）

A、 $(220 + x) (5000 - 5 x) = 1380000$ B、 $(220 + x) (5000 - 5 x) = 138$ C、 $(220 + x) (5000 - 50 x) = 138$ D、 $(220 + x) (5000 - 50 x) = 138000$

查看解析
16、如图，将 $△ A B C$ 绕着点 $C$ 按顺时针方向旋转 $20 °$ ， $B$ 点落在 $B^{'}$ 位置， $A$ 点落在 $A^{'}$ 位置，若 $A C ⊥ A^{'} B^{'}$ ，则 $∠ B A C$ 的度数是（）

A、 $50 °$ B、 $60 °$ C、 $70 °$ D、 $80 °$

查看解析
17、一元二次方程 $x^{2} - x - 1 = 0$ 的两个实数根中较大的根是（）

A、 $1 + \sqrt{5}$ B、 $\frac{- 1 + \sqrt{5}}{2}$ C、 $\frac{1 - \sqrt{5}}{2}$ D、 $\frac{1 + \sqrt{5}}{2}$

查看解析
18、抛物线 $y = - \frac{1}{2} x^{2} - 1$ 的开口方向（）

A、向下 B、向上 C、向左 D、向右

查看解析
19、若二次函数y＝ax²的图象经过点（1，﹣2），则它也经过（）

A、（﹣1，﹣2） B、（﹣1，2） C、（1，2） D、（2，1）

查看解析
20、下列函数是二次函数的是（）

A、 $y = - 2 x + 3$ B、 $y = 5 x^{2} + 1$ C、 $y = \frac{1}{x^{2}}$ D、 $y = x^{3} + 2 x^{2} - 1$

查看解析

上一页 187 188 189 190 191 下一页跳转

x	…	-2	-1	0	1	2	…
y	…	0	-4	-4	0	8	…