华东师大版数学八年级上学期期中仿真模拟试卷一(范围:10.1-12.2)
试卷更新日期:2025-09-13 类型:期中考试
一、选择题:每题3分,共36分
-
1. 在0.7, , , , , 2.010010001六个实数中,无理数的个数有( )A、5个 B、4个 C、3个 D、2个2. 关于立方根,下列说法正确的是( )A、正数有两个立方根 B、立方根等于它本身的数只有0 C、负数的立方根是负数 D、负数没有立方根3. 下列各式中,计算正确的是( )A、 B、 C、 D、4. 设 , , 其中 , 给出以下结论:①;②当时,;则下列判断正确的是( )A、①,②都对 B、①,②都错 C、①对,②错 D、①错,②对5. 嘉嘉先画出了 , 再利用尺规作图画出了 , 使 . 图1~图3是其作图过程.
(1)以点为圆心,以适当长为半径画弧,交AB于点 , 交AC于点 .
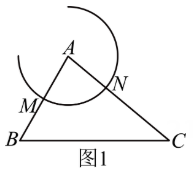
(2)以点为圆心,以MN长为半径画弧,与(1)中的弧交于点 , 作射线AP.
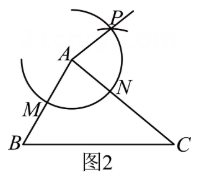
(3)以点A为圆心,先以AB长为半径画弧,与边AC交于点 , 再以AC长为半径画弧,与射线AP交于点 , 连接DE .
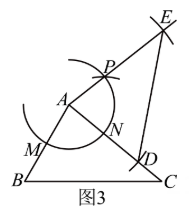
在嘉嘉的作法中,可直接判定的依据是( )
A、SSS B、SAS C、ASA D、AAS6. 已知 , , 则值为( )A、7 B、10 C、 D、7. 将多项式分解因式,应提取的公因式是( )A、 B、 C、 D、8. 一个正方形的面积是8,估计它的边长大小在( )A、1与2之间 B、2与3之间 C、3与4之间 D、4与5之间9. 已知一个正数的两个不同的平方根分别是和 , 则的值为( )A、2 B、4 C、25 D、10. 一副含角和角的直角三角板如图摆放,则的度数为( ) A、 B、 C、 D、11. 已知 , 则的值是( )A、4 B、8 C、17 D、3412. 如图,在和中, , , , 过作 , 垂足为 , 交的延长线于点 , 连接 . 四边形的面积为64, . 则的长是( )
A、 B、 C、 D、11. 已知 , 则的值是( )A、4 B、8 C、17 D、3412. 如图,在和中, , , , 过作 , 垂足为 , 交的延长线于点 , 连接 . 四边形的面积为64, . 则的长是( ) A、8 B、 C、 D、6
A、8 B、 C、 D、6二、填空题:每题3分,共18分
-
13. 的算术平方根是14. 将命题“两个全等三角形的周长相等”改写成“如果…那么…”的形式.15. 若 , 为实数,且 , 则的值为 .16. 若关于的多项式展开后不含有一次项,则实数的值为 .17. 如图, , 和分别是和的中点,连结 , 并延长,分别交于 , , 若四边形的面积为 , 那么 .
 18. 如图①,在边长为a的正方形中剪去一个边长为b的小正方形,然后把剩下部分沿图中虚线剪开后拼成如图②所示的梯形、通过计算图①、图②中阴影部分的面积,可以得到的代数恒等式为 .
18. 如图①,在边长为a的正方形中剪去一个边长为b的小正方形,然后把剩下部分沿图中虚线剪开后拼成如图②所示的梯形、通过计算图①、图②中阴影部分的面积,可以得到的代数恒等式为 .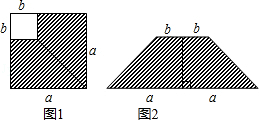
三、解答题:共8题,共66分
-
19. 计算.(1)、;(2)、6a6b4÷3a3b4+a2•(-5a).20. 因式分解:(1)、;(2)、 .21. 先化简,再求值: , 其中 .22. 已知一个正数的平方根分别是和 , 又的立方根为 .(1)、求a , b的值;(2)、求的算术平方根.23. 如图,已知 . 求证:F是的中点.
 24. 如图,阳阳为了测量楼高 , 在旗杆与楼之间选定一点 , 使 , 量得点到楼底距离与旗杆高度都为 , 旗杆与楼之间的距离 , 求楼高 .
24. 如图,阳阳为了测量楼高 , 在旗杆与楼之间选定一点 , 使 , 量得点到楼底距离与旗杆高度都为 , 旗杆与楼之间的距离 , 求楼高 . 25. 【探索发现】
25. 【探索发现】数学活动课上,老师准备了如图的一个长为 , 宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按如图所示的形状拼成一个大正方形.
 (1)、图中的阴影部分正方形的边长是(用含 , 的代数式表示);(2)、观察图 , 图 , 请写出 , , 之间的等量关系是;(3)、【解决问题】
(1)、图中的阴影部分正方形的边长是(用含 , 的代数式表示);(2)、观察图 , 图 , 请写出 , , 之间的等量关系是;(3)、【解决问题】若 , , 且 , 则;
(4)、【实际应用】学校计划用一块梯形区域开展科技节活动,如图所示.已知于点 , , . 计划在和区域内展示无人机和机器人表演,在和区域内分别是主舞台和观众,经测无人机和机器人表演区域的面积和为平方米,米,求主舞台和观众区的面积和.
 26. 如图,已知中, , 厘米,厘米,点为的中点,如果点在线段上以每秒厘米的速度由点向点运动,同时,点在线段上以每秒厘米的速度由点向点运动,设运动时间为(秒)().
26. 如图,已知中, , 厘米,厘米,点为的中点,如果点在线段上以每秒厘米的速度由点向点运动,同时,点在线段上以每秒厘米的速度由点向点运动,设运动时间为(秒)().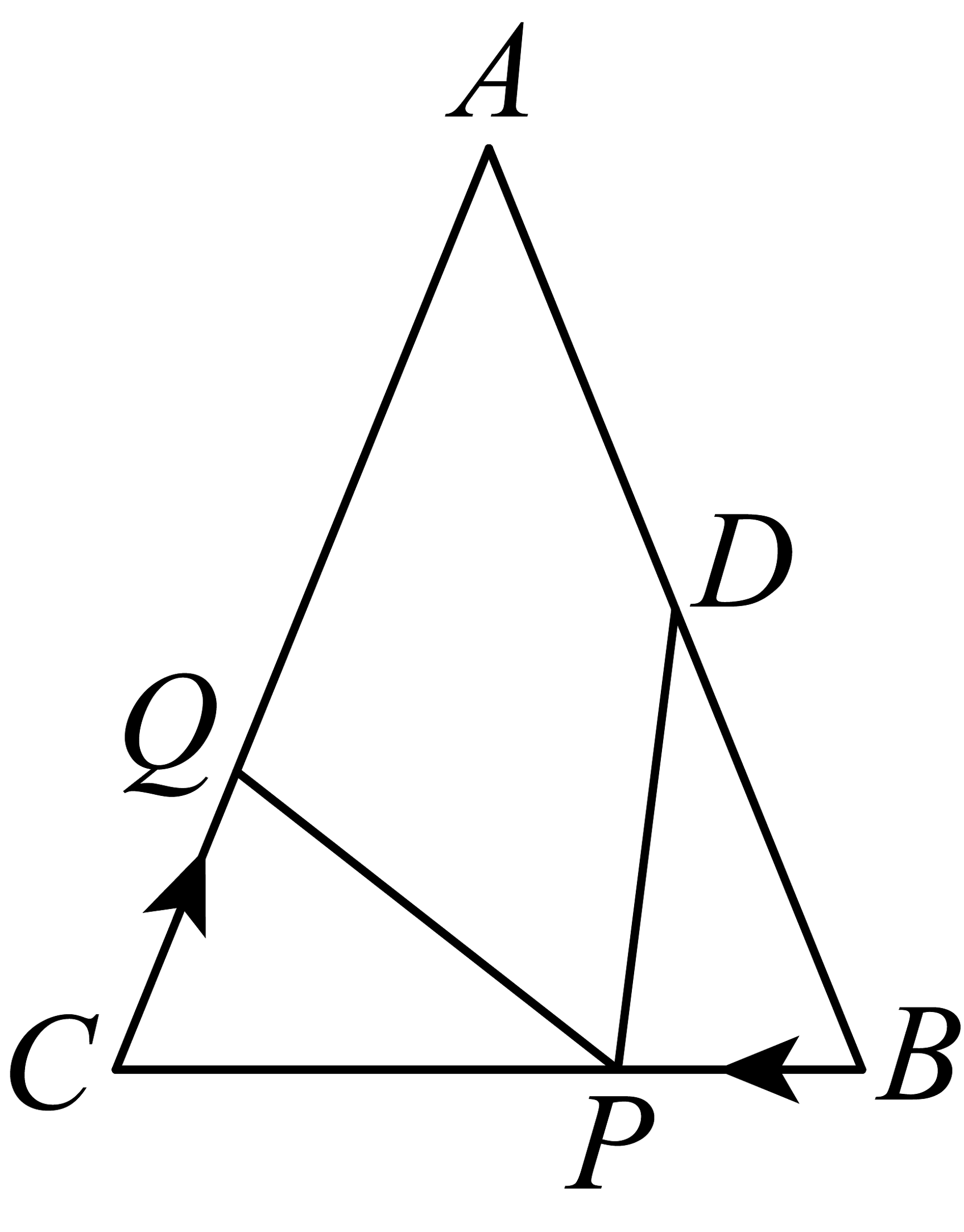 (1)、用含的代数式表示的长度:________.(2)、若点、的运动速度相等,经过秒后,与是否全等,请说明理由;(3)、若点、的运动速度不相等,当点的运动速度为多少时,能够使与全等?
(1)、用含的代数式表示的长度:________.(2)、若点、的运动速度相等,经过秒后,与是否全等,请说明理由;(3)、若点、的运动速度不相等,当点的运动速度为多少时,能够使与全等?