浙教版数学八年级上学期重难点复习7:一次函数图象的几何变换
试卷更新日期:2025-09-15 类型:复习试卷
一、一次函数图象中的平移问题
-
1. 将直线l:y=-2(x+3)经过适当变换后得到直线,要使经过原点,则可以将直线l( )A、向上平移3个单位 B、向下平移6个单位 C、向右平移3个单位 D、向左平移6个单位2. 如图 , 在平面直角坐标系中,等腰在第一象限,且 轴,直线从原点出发沿轴正方向平移,在平移过程中,直线被截得的线段长度与直线在轴上平移的距离的函数图象如图所示,那么的面积为
 3. 已知直线与函数的图像相交于两点(点在点左侧).
3. 已知直线与函数的图像相交于两点(点在点左侧).
(1)点的坐标是 .
(2)若坐标原点为点 , 将两个函数图象向右平移个单位,点平移后分别对应点 , 连接 , 当最大时,的值为 .
4. 图象法是函数的表示方法之一,下面我们就一类特殊的函数图象展开探究.画函数的图象,经历列表、描点、连线过程得到函数图象如图所示:
探究发现:函数的图象是由向右平移个单位得到;
函数的图象是由向上平移个单位得到.

(1)函数的最小值为;
(2)函数在中有最小值 , 则的值是 .
5. 如图,直线与y轴交于点 , 与x轴交于点 , 直线以每秒1个单位长度的速度沿y轴正方向平移,平移时交线段于点D , 交线段于点C , 当点C与点B重合时结束运动. (1)、求出直线的关系式;(2)、如图1,若直线的函数关系式为 , P是直线上一点,当的面积等于的面积时,求点P的坐标;
(1)、求出直线的关系式;(2)、如图1,若直线的函数关系式为 , P是直线上一点,当的面积等于的面积时,求点P的坐标;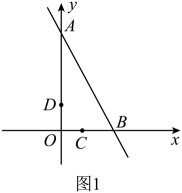 (3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为 . 求出当t为何值时,是等腰三角形?
(3)、如图2,在直线运动过程中,过点D作轴交于点E , 连接 , 设运动时间为 . 求出当t为何值时,是等腰三角形?
二、一次函数图象中的对称、翻折问题
-
6. 若直线 与直线 关于直线 对称,则k、b值分别为( )A、 、 B、 、 C、 、 D、 、7. 如图,在平面直角坐标系中有两条直线:: , : , 对点作如下操作.第1步,作点关于的对称点;第2步,作关于的对称点;第3步,再作关于的对称点;第4步,再作关于的对称点以此类推,问:点的坐标为( )
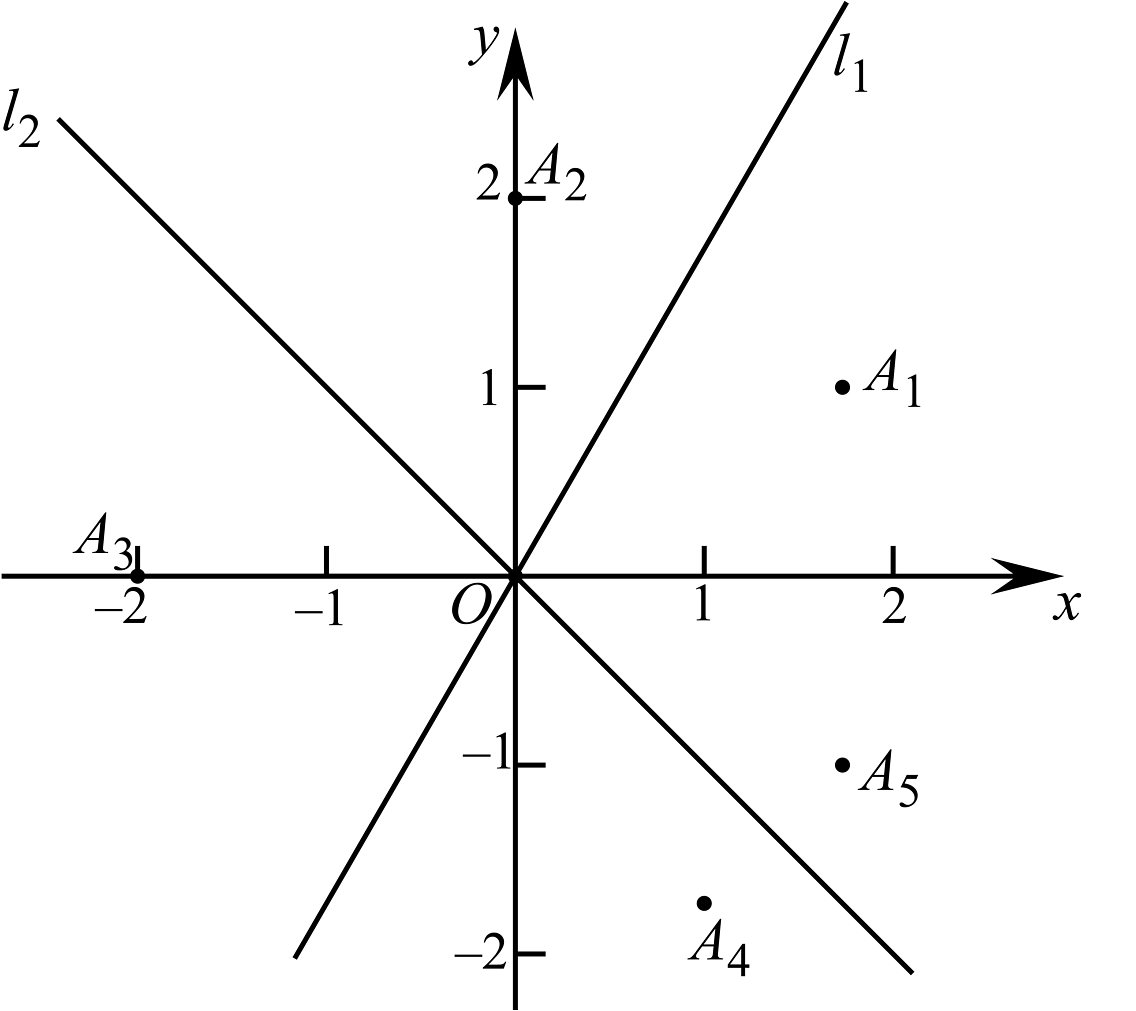 A、 B、 C、 D、8. 定义,图象与x轴有两个交点的函数y=叫做关于直线x=m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B例如:如图:直线l:x=1,关于直线l的对称函数y=与该直线l交于点C,当直线y=x与关于直线x=m的对称函数有两个交点时,则m的取值范围是( )
A、 B、 C、 D、8. 定义,图象与x轴有两个交点的函数y=叫做关于直线x=m的对称函数,它与x轴负半轴交点记为A,与x轴正半轴交点记为B例如:如图:直线l:x=1,关于直线l的对称函数y=与该直线l交于点C,当直线y=x与关于直线x=m的对称函数有两个交点时,则m的取值范围是( ) A、0≤m≤ B、-2<m≤ C、-2<m≤2 D、-4<m<09. 已知,如图,直线AB:y=kx-k-4,分别交平面直角坐标系于A,B两点,直线CD.y=-2x+2与坐标轴交于C,D两点,两直线交于点E(a,-a);点M是y轴上一动点,连接ME,将△AEM沿ME翻折,A点对应点刚好落在x轴负半轴上,则ME所在直线解析式为( )
A、0≤m≤ B、-2<m≤ C、-2<m≤2 D、-4<m<09. 已知,如图,直线AB:y=kx-k-4,分别交平面直角坐标系于A,B两点,直线CD.y=-2x+2与坐标轴交于C,D两点,两直线交于点E(a,-a);点M是y轴上一动点,连接ME,将△AEM沿ME翻折,A点对应点刚好落在x轴负半轴上,则ME所在直线解析式为( ) A、y=
A、y= x﹣
x﹣ B、y=2x﹣6
C、y=
B、y=2x﹣6
C、y= x﹣
x﹣ D、y=x﹣
D、y=x﹣ 10. 一次函数的图象,沿着过点且垂直于x轴的直线翻折后经过点 , 则b的值为 .11. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、点 , 点在轴的负半轴上,将沿翻折,点恰好落在轴正半轴上的点处,则点的坐标为 .
10. 一次函数的图象,沿着过点且垂直于x轴的直线翻折后经过点 , 则b的值为 .11. 如图,在平面直角坐标系中,直线与轴、轴分别交于点、点 , 点在轴的负半轴上,将沿翻折,点恰好落在轴正半轴上的点处,则点的坐标为 . 12. 如图,直线:与坐标轴交于A、B两点,点D为第一象限内一点,连接且轴,过点且平行于x轴的直线l交于点C,交于点F,连接 , , 将沿着直线翻折,得到 , 点E正好落在直线l上,若 , 则的长为 .
12. 如图,直线:与坐标轴交于A、B两点,点D为第一象限内一点,连接且轴,过点且平行于x轴的直线l交于点C,交于点F,连接 , , 将沿着直线翻折,得到 , 点E正好落在直线l上,若 , 则的长为 .
三、一次函数图象中的旋转问题
-
13. 如图, 直线 与 轴, 轴分别交于 两点, 把 绕点 顺时针旋转 后得到 , 则点 的坐标是( )
 A、 B、 C、 D、
A、 B、 C、 D、