4.1《函数》—北师大版数学八年级上册课堂分层训练
试卷更新日期:2025-09-15 类型:同步测试
一、基础夯实
-
1. 如图选项中,有五种形状不同的容器,从容器口以均匀的速度倒入某溶液,若液面高度h 关于时间t的函数图象如图所示,则该容器的形状为( ).
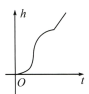 A、
A、 B、
B、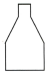 C、
C、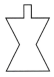 D、
D、 E、
E、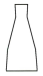 2. “人间四月芳菲尽,山寺桃花始盛开”,证明温度随着海拔的升高而降低,已知某地面温度为 , 且每升高1千米温度下降 , 则山上距离地面千米处的温度为( )A、 B、 C、 D、3. 函数的自变量x的取值范围是( )A、 B、 C、 D、4. 当时,函数的值是( )A、 B、 C、0 D、15. 汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程s(千米)与行驶时间t(小时)的函数关系及自变量的取值范围是.6. 某复印店复印收费y(元)与复印面数x面的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费 元.
2. “人间四月芳菲尽,山寺桃花始盛开”,证明温度随着海拔的升高而降低,已知某地面温度为 , 且每升高1千米温度下降 , 则山上距离地面千米处的温度为( )A、 B、 C、 D、3. 函数的自变量x的取值范围是( )A、 B、 C、 D、4. 当时,函数的值是( )A、 B、 C、0 D、15. 汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程s(千米)与行驶时间t(小时)的函数关系及自变量的取值范围是.6. 某复印店复印收费y(元)与复印面数x面的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费 元. 7. 由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的函数关系如图所示.
7. 由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少.水库的蓄水量V(万立方米)与干旱持续时间t(天)之间的函数关系如图所示.
根据图象回答下列问题:
(1)、干旱持续10天时,蓄水量为万立方米.(2)、如果蓄水量小于400万立方米时,将发出严重干旱警报,那么干旱天后将发出严重干旱警报.8. 小南一家到某度假村度假.小南和妈妈坐公交车先出发,爸爸自驾车沿着相同的道路后出发.爸爸到达度假村后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往度假村(取东西的时间忽略不计).如下图是他们离家的距离s(km)与小南离家的时间t(h)的关系图.请根据图回答下列问题:(1)图中的自变量是_________,因变量是_________,小南家到该度假村的距离是_____km.
(2)小南出发___________小时后爸爸驾车出发,爸爸驾车的平均速度为___________km/h,图中点A表示 .
(3)小南从家到度假村的路途中,当他与爸爸相遇时,离家的距离约是___________km.

二、能力提升
-
9. 某市储运部紧急调拨一批物资,调进物资共用4小时,调进物资2小时后开始调出物资(调进物资与调出物资的速度均保持不变).储运部库存物资s(吨)与时间t(小时)之间的函数关系如图所示,这批物资从开始调进到全部调出所需要的时间是( ).
 A、4 小时 B、4.4 小时 C、4.8小时 D、5 小时10. 甲、乙两人沿同一跑道从A处跑到B处.乙比甲先出发2分钟,甲的速度为每分钟150米.若两人之间的路程y(米)与甲出发的时间x(分钟)的关系如图所示,则A、B两地的路程为( )
A、4 小时 B、4.4 小时 C、4.8小时 D、5 小时10. 甲、乙两人沿同一跑道从A处跑到B处.乙比甲先出发2分钟,甲的速度为每分钟150米.若两人之间的路程y(米)与甲出发的时间x(分钟)的关系如图所示,则A、B两地的路程为( ) A、1800米 B、2000米 C、2400米 D、2500米11. 材料:甲开汽车,乙骑自行车从地沿一条笔直的公路匀速前往地,乙比甲先出发.设乙行驶的时间为 , 甲,乙两人之间的距离关于时间的函数图象如图所示.根据材料,获得正确的信息是( )
A、1800米 B、2000米 C、2400米 D、2500米11. 材料:甲开汽车,乙骑自行车从地沿一条笔直的公路匀速前往地,乙比甲先出发.设乙行驶的时间为 , 甲,乙两人之间的距离关于时间的函数图象如图所示.根据材料,获得正确的信息是( ) A、甲行驶的速度是 B、在甲出发后追上乙 C、 , 两地之间的距离为 D、甲比乙少行驶2小时12. 公路旁依次有 , , 三个村庄,小明和小红骑自行车分别从A村、村同时出发匀速前往村(到了村不继续往前骑行,也不返回),如图所示, , 分别表示小明和小红与村的距离和骑行时间之间的函数关系,下列结论:
A、甲行驶的速度是 B、在甲出发后追上乙 C、 , 两地之间的距离为 D、甲比乙少行驶2小时12. 公路旁依次有 , , 三个村庄,小明和小红骑自行车分别从A村、村同时出发匀速前往村(到了村不继续往前骑行,也不返回),如图所示, , 分别表示小明和小红与村的距离和骑行时间之间的函数关系,下列结论:
①A,两村相距;
②小明每小时比小红多骑行;
③出发后两人相遇;
④图中 .
其中正确的是( )
A、②④ B、①③④ C、①②③ D、①②③④13. 有一块长方形菜园 , 一边利用足够长的墙,另三边用长度为的篱笆围成,设长方形的长为 , 宽为 , 则下列函数图象能反映与关系的是 A、
A、 B、
B、 C、
C、 D、
D、 14. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是.
14. 如图1,在中,动点从点出发沿折线匀速运动至点后停止.已知点的运动速度是每秒2个单位长度,设点运动时间为 , 线段的长度为 , 图2是与的函数关系的大致图象,其中点为曲线的最低点,则的高长是. 15. 如图,某链条每节长为 , 每两节链条相连接部分重叠的圆的直径为 , 按这种连接方式,x节链条总长度为 , 则y关于x的函数关系式是.
15. 如图,某链条每节长为 , 每两节链条相连接部分重叠的圆的直径为 , 按这种连接方式,x节链条总长度为 , 则y关于x的函数关系式是. 16. 甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶, 快递车到达乙地后,卸完物资并另装货物共用了 45 分钟,然后按原路以另一速度返回,直至与货车相遇.已知货车行驶速度为 60 km/h,两车间的距离 y(km) 与货车行驶时间 x(h) 之间的函数图象如图所示:
16. 甲地宏达物流公司的快递车和货车同时从甲地出发,以各自的速度沿快速通道向乙地匀速行驶, 快递车到达乙地后,卸完物资并另装货物共用了 45 分钟,然后按原路以另一速度返回,直至与货车相遇.已知货车行驶速度为 60 km/h,两车间的距离 y(km) 与货车行驶时间 x(h) 之间的函数图象如图所示:
给出以下四个结论:
① 快递车从甲地到乙地的速度是 100 km/h;
② 甲、乙两地之间的距离是 80 km;
③ 图中点 B 的坐标为 ( , 35);
④ 快递车从乙地返回时的速度为 90 km/h.
其中正确的是(填序号).
17. 下列各题中分别有几个变量?其中某个变量能看成另一个变量的函数吗?若能,请写出自变量的取值范围.(1)、北京市某天气温的变化情况如图所示; (2)、在平整的路面上,某型号汽车紧急刹车后仍会滑行 sm,一般地,有经验公式 其中v表示刹车前汽车的速度(单位:km/h);(3)、在国内,将质量在100g以内的普通信函投寄到外埠,应付邮资见下表:
(2)、在平整的路面上,某型号汽车紧急刹车后仍会滑行 sm,一般地,有经验公式 其中v表示刹车前汽车的速度(单位:km/h);(3)、在国内,将质量在100g以内的普通信函投寄到外埠,应付邮资见下表:信件质量m/g
0<m≤20
20<m≤40
40<m≤60
60<m≤80
80<m≤100
邮资y/元
1.20
2.40
3.60
4.80
6.00
18. 甲乙两船从A港口出发匀速开往B港口,在整个过程中,两船离开A港口的距离与时间的对应关系如图所示. (1)、甲乙两船的航速分别是多少?(2)、乙船出发多久可以追上甲船?(3)、直接写出甲乙两船何时相距 .19. 如图是小明骑自行车从家到学校所行路程s与时间t的折线图,请根据图象回答下列问题:
(1)、甲乙两船的航速分别是多少?(2)、乙船出发多久可以追上甲船?(3)、直接写出甲乙两船何时相距 .19. 如图是小明骑自行车从家到学校所行路程s与时间t的折线图,请根据图象回答下列问题: (1)、这个折线图反映了哪两个变量之间的关系?路程s可以看成时间t的函数吗?(2)、求当t=8分钟时的函数值.(3)、当10≤t≤15时,对应的函数值是多少?并说明它的实际意义.(4)、小明家离学校多远?小明骑自行车上学共用了多少分钟?
(1)、这个折线图反映了哪两个变量之间的关系?路程s可以看成时间t的函数吗?(2)、求当t=8分钟时的函数值.(3)、当10≤t≤15时,对应的函数值是多少?并说明它的实际意义.(4)、小明家离学校多远?小明骑自行车上学共用了多少分钟?三、拓展培优
-
20. “龟兔赛跑”的故事同学们都非常熟悉,图中的线段和折线表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
 (1)、填空:折线表示赛跑过程中的路程与时间的关系,线段表示赛跑过程中的路程与时间的关系.赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)、乌龟用了多少分钟追上了正在睡觉的兔子?(4)、兔子醒来,以48千米时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?21. 甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按 折出售,乙商场对一次购物中价格超过 元后的部分打 折.(1)、以 (单位:元)表示商品原价,(单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数关系式;(2)、当商品的原价为250时,在哪家商场通过打折后更划算.(3)、当商品的原价为多少元时,两家商场打折后的价格相同.
(1)、填空:折线表示赛跑过程中的路程与时间的关系,线段表示赛跑过程中的路程与时间的关系.赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)、乌龟用了多少分钟追上了正在睡觉的兔子?(4)、兔子醒来,以48千米时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?21. 甲、乙两家商场平时以同样价格出售相同的商品,新冠疫情期间,为了减少库存,甲、乙两家商场打折促销,甲商场所有商品按 折出售,乙商场对一次购物中价格超过 元后的部分打 折.(1)、以 (单位:元)表示商品原价,(单位:元)表示实际购物金额,分别就两家商场的让利方式写出 关于 的函数关系式;(2)、当商品的原价为250时,在哪家商场通过打折后更划算.(3)、当商品的原价为多少元时,两家商场打折后的价格相同.