相关试卷

1、如图，观察下列几何体并回答问题：

(1)、 $n$ 棱柱有个面、条棱、个顶点， $n$ 棱锥有个面、条棱、个顶点．

(2)、所有像三棱柱、四棱柱、六棱柱、三棱锥等这样由四个或四个以上多边形所围成的立体图形叫作多面体．经过前人们归纳总结发现，多面体的面数 $F$ 、顶点个数 $V$ 以及棱的条数 $E$ 存在着一定的数量关系，请直接写出这个关系式．

查看解析
2、蒙古包，作为蒙古族传统的居住形式，承载着浓厚的游牧文化和历史底蕴．它的上面近似于圆锥形，下面近似于圆柱形．如图，一个蒙古包圆柱底面的周长是 $20 π$ 米，高是 $2$ 米，圆锥的高是 $1.2$ 米．

(1)、蒙古包的上面圆锥部分的侧面展开图是_______（填图形名称）；下面圆柱部分的侧面展开图是_______（填图形名称），圆柱部分的侧面展开图的面积是_____平方米（结果保留 $π$ ）．

(2)、这个蒙古包的体积是多少立方米？（结果保留 $π$ ）

查看解析
3、奥运会是集体育精神、民族精神和国际主义精神于一身的世界级运动盛会，象征着世界的和平、团结和友谊．今年巴黎奥运会虽在国外进行，但关注度仍然非常高，人们通过观看电视直播的方式关注这一体育盛会．据中国视听大数据调查显示，电视直播总观看户次超46亿，下表为8月份第一周的电视直播观看户次，其中7月31日观看户次为 $2.74$ 亿．（正数表示比前一天多的户次，负数表示比前一天少的户次）
日期
8月1日
8月2日
8月3日
8月4日
8月5日
8月6日
8月7日
奥运会电视直播观看户次/亿
$- 0.50$
$+ 0.35$
$+ 2.94$
$- 1.14$
$- 0.17$
$- 0.67$
$- 0.81$

(1)、8月2日的电视直播观看户次为亿．

(2)、这一周里，奥运会电视直播观看户次最多的一天达到亿，观看户次最少的一天达到亿．

(3)、据上表统计，这一周内奥运会电视直播总观看户次为多少亿？

查看解析
4、如图是由棱长都为 $1cm$ 的小立方块搭成的几何体．

(1)、这个几何体由个小立方块构成．

(2)、请在方格中画出从三个方向看到的该几何体的形状图．

查看解析
5、计算： ${(- 1)}^{2024} + \frac{1}{2} \times (- 2^{3} - 4 \div 2)$ ．

查看解析
6、在 $- 1.2345678 \dots$ ， $\frac{24}{7}, 0.161161116 \dots$ ， $\frac{π}{2}$ 中，有理数是．

查看解析
7、一个正方体六个面上分别写着A，B，C，D，E，F，如图为这个正方体三种不同的摆法，则字母A对面的字母是．

查看解析
8、如图所示是一个运算程序示意图．若第一次输入k的值为25，则第2024次输出的结果是（）

A、1 B、5 C、25 D、1或5

查看解析
9、如图是由一些同样大小的三角形按照一定规律所组成的图形，第1个图有4个三角形，第2个图有7个三角形，第3个图有10个三角形……按照此规律排列下去，第674个图中三角形的个数是（）个

A、2026 B、2025 C、2024 D、2023

查看解析
10、若 $|3 - x|$ 与 ${(y + 1)}^{2}$ 的值互为相反数，则 $x y - (y - x)$ 的值是（）

A、7 B、 $- 7$ C、1 D、 $- 1$

查看解析
11、下列各组单项式中，为同类项的是（）

A、 $a^{3}$ 与 $a^{2}$ B、 $2 x y$ 与 $2 x$ C、 $a^{2} b$ 与 $2 b a^{2}$ D、 $- 3$ 与a

查看解析
12、小英在家里整理内务时发现：把一些相同规格的塑料凳子整齐地叠放在水平地面上，这摞塑料凳子的高度随着凳子的数量变化有一定的关系．于是小英对凳子的高度进行测量，具体变化的情况如下表所示：
凳子的数量 $/$ 个
$1$
$2$
$3$
$4$
$5$
$\dots$
高度 $/ cm$
$50$
$55$
$60$
$65$
$70$
$\dots$

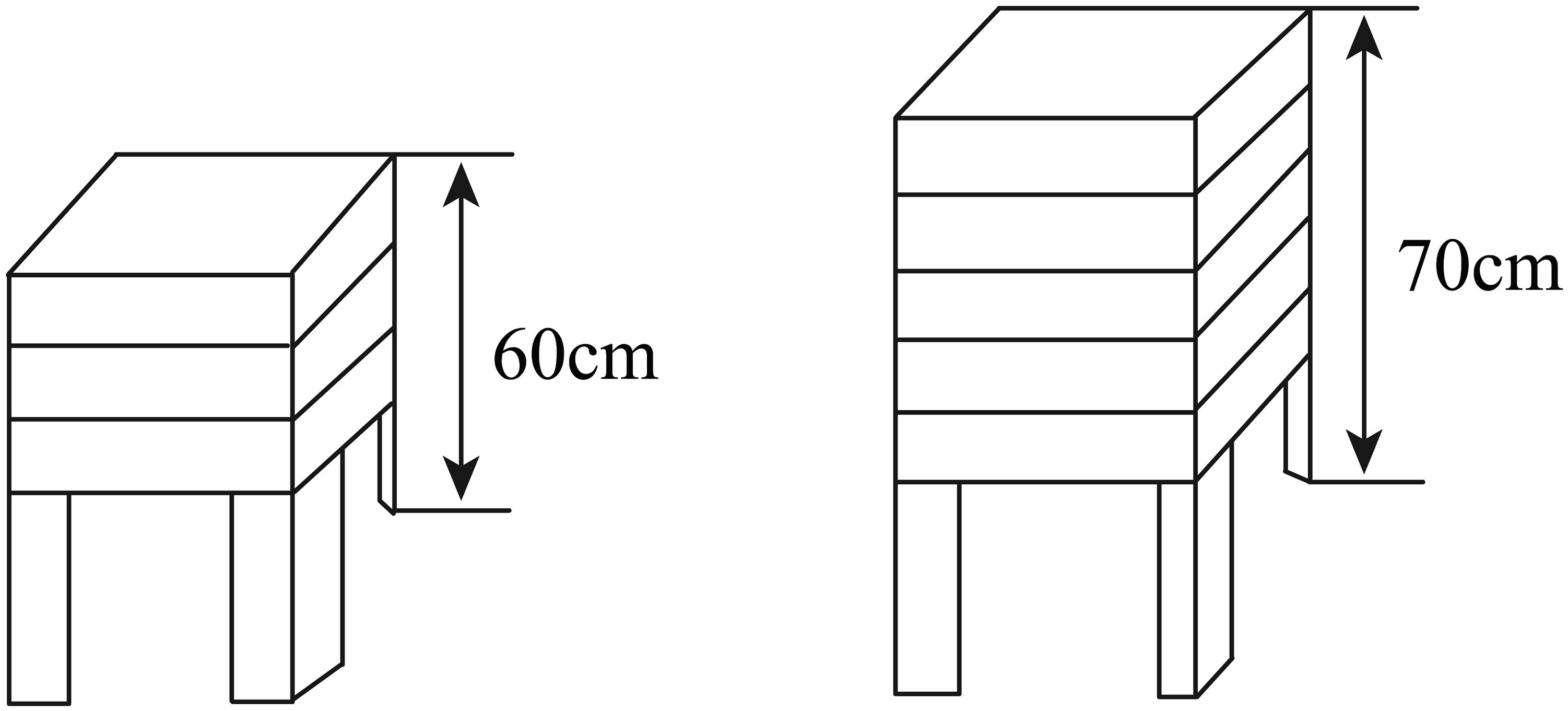(1)、上述两个变量之间的关系中，哪个是自变量？哪个是因变量？

(2)、用 $h$ （ $cm$ ）表示这摞凳子的高度， $x$ （个）表示这摞凳子的数量，请写出 $h$ 与 $x$ 之间的函数关系式；

(3)、当这摞凳子的高度为 $105 cm$ 时，求这摞凳子的数量．

查看解析
13、已知 $2 a + 1$ 的立方根是 $- 5$ ， $a + 2 b$ 的算术平方根是 $3$ ， $c$ 是 $\sqrt{15}$ 的整数部分．

(1)、求 $a ， b ， c$ 的值；

(2)、求 $a + 2 b + c$ 的平方根．

查看解析
14、小明作为蓝信封行动的通信志愿者，有一次制作了一张面积为 $81 {cm}^{2}$ 的正方形明信片想寄给对接的乡村小朋友．已知信封的长、宽之比为 $5 : 3$ ，面积为 $150 {cm}^{2}$ ．

(1)、求长方形信封的长和宽；

(2)、判断小明能否将这张明信片不折叠就放入此信封，并说明理由．

查看解析
15、计算： $- \sqrt{16} + |\sqrt{3} - 3| - \sqrt[3]{- 8} + 2 \sqrt{3}$ ．

查看解析
16、在平面直角坐标系中，若点 $M (1, 8)$ 与点 $N (m, 8)$ 之间的距离是 $5$ ，则 $m$ 的值是．

查看解析
17、将直线 $y = 5 x + 1$ 向上平移 $6$ 个单位长度后，得到的新直线的解析式是．

查看解析
18、比较大小 $\sqrt{24}$ 5（填“ $>$ ”“ $<$ ”或“ $=$ ”）

查看解析
19、已知 $m = \sqrt{9} + \sqrt{3}$ ，则 $m$ 的小数部分是（）

A、 $\sqrt{3}$ B、 $\sqrt{3} + 1$ C、 $\sqrt{3} - 1$ D、 $4$

查看解析
20、下列函数中，是一次函数的是（）
① $y = 3 x$ ；② $y = x^{2} + 2$ ；③ $y = 2 x + 1$ ；④ $y = \frac{4}{x}$ ．

A、②④ B、②③ C、①③ D、①②

查看解析

上一页 186 187 188 189 190 下一页跳转

日期	8月1日	8月2日	8月3日	8月4日	8月5日	8月6日	8月7日
奥运会电视直播观看户次/亿	$- 0.50$	$+ 0.35$	$+ 2.94$	$- 1.14$	$- 0.17$	$- 0.67$	$- 0.81$

凳子的数量 $/$ 个	$1$	$2$	$3$	$4$	$5$	$\dots$
高度 $/ cm$	$50$	$55$	$60$	$65$	$70$	$\dots$