-
1、 如图， 连接AC， AD， BD， BE， CE， 求证
-
2、 如图， 在△ABC中， BE，CF是角平分线， 且BE， CF 相交于点G. 求证：
(1)、(2)、 -
3、 如图， 在△ABC 中， AD 是高， AE， BF 是角平分线， 且AE， BF 相交于点O，∠BAC=50°， ∠C=70°. 求∠DAC 和∠BOA 的度数.
-
4、 如图， 在△ABC 中，∠C=∠ABC=2∠A， BD是边AC上的高. 求∠DBC 的度数.
-
5、 如图， ∠B=42°， ∠A 比∠1小10°， ∠ACD=64°. 求证AB∥CD.
-
6、求出下列各图形中x的值.(1)、
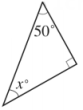(2)、
(3)、
-
7、如图， 填空：
由三角形两边的和大于第三边，得AB+AD> ， PD+CD>.
将不等式左边、右边分别相加，得AB+AD+PD+CD> ， 即 AB+AC>.
-
8、 如图， 在△ABC中， AD， AE 分别是边BC 上的中线和高，AE=2， S△ABD =1.5. 求 BC 和DC 的长.
-
9、下列四个条件：
①在△ABC 中， ∠A， ∠B 都是锐角；
②△ABC的三个内角的度数之比是1：2：3；
③在△ABC中， ∠A-∠B=∠C；
④△ABC的三个外角的度数之比是3：4：5.
其中能确定△ABC 是直角三角形的是(只填序号).
-
10、 如图， 已知点A， B在直线a上， 点C， D， E在直线b上.以点A，B，C，D，E中的任意三点作为三角形的顶点，一共可以组成多少个三角形?分别写出这些三角形
-
11、 如图， AB=BC=CD=DA=AC， 找出图中的等腰三角形和等边三角形.
-
12、 如图， 在△ABC 中， AD⊥BC， 垂足为D，∠BAC 是钝角， E 是DC 上一点， 且∠BAE 是锐角.
(1)、图中有几个三角形?用符号表示这些三角形.(2)、找出图中的锐角三角形、直角三角形和钝角三角形. -
13、图中有几个三角形?用符号表示这些三角形.
-
14、如图，写出以∠A 为角的三角形，写出以BC 为边的三角形.
-
15、 如图， 在△ABC 中， ∠BAC 是直角， AD⊥BC， 垂足为D， 点E 在线段BD上，找出图中的锐角三角形、直角三角形和钝角三角形.
-
16、 如图， 在△ABC 中， AB=BC=CA， 点O在△ABC 内， OA=OB=OC，找出图中的等腰三角形和等边三角形.
-
17、如图， 在△ABC 中， 点D 在边BC上， BD=AD=DC=AC.
(1)、写出以点 C 为顶点的三角形；(2)、写出以AB 为边的三角形；(3)、找出图中的等腰三角形和等边三角形. -
18、【阅读材料】进位制是人们为了记数和运算方便而约定的记数系统．对于任何一种进制﹣X进制，就表示某一位置上的数运算时是逢X进一位．十进制是逢十进一，十六进制是逢十六进一，以此类推，X进制就是逢X进一．为与十进制进行区分 ．
【方法指导】类比于十进制，我们可以知道：X进制表示的数中，右起第一位上的1表示 ， 第二位上的1表示 ， 第三位上的1表示 ， 第四位上的1表示 ， 故 ， 即：转化为十进制表示的数为 ． 如： ． 根据材料，完成以下问题：
(1)、把下列进制表示的数转化为十进制表示的数： ；(2)、根据有理数的加法运算法则，计算；(3)、若一个五进制三位数与八进制三位数之和能被13整除（ ， 且a，b均为整数），求a的值． -
19、日历上的规律：下图是2023年11月的日历，图中的阴影区域是在日历中选取的一块九宫格．
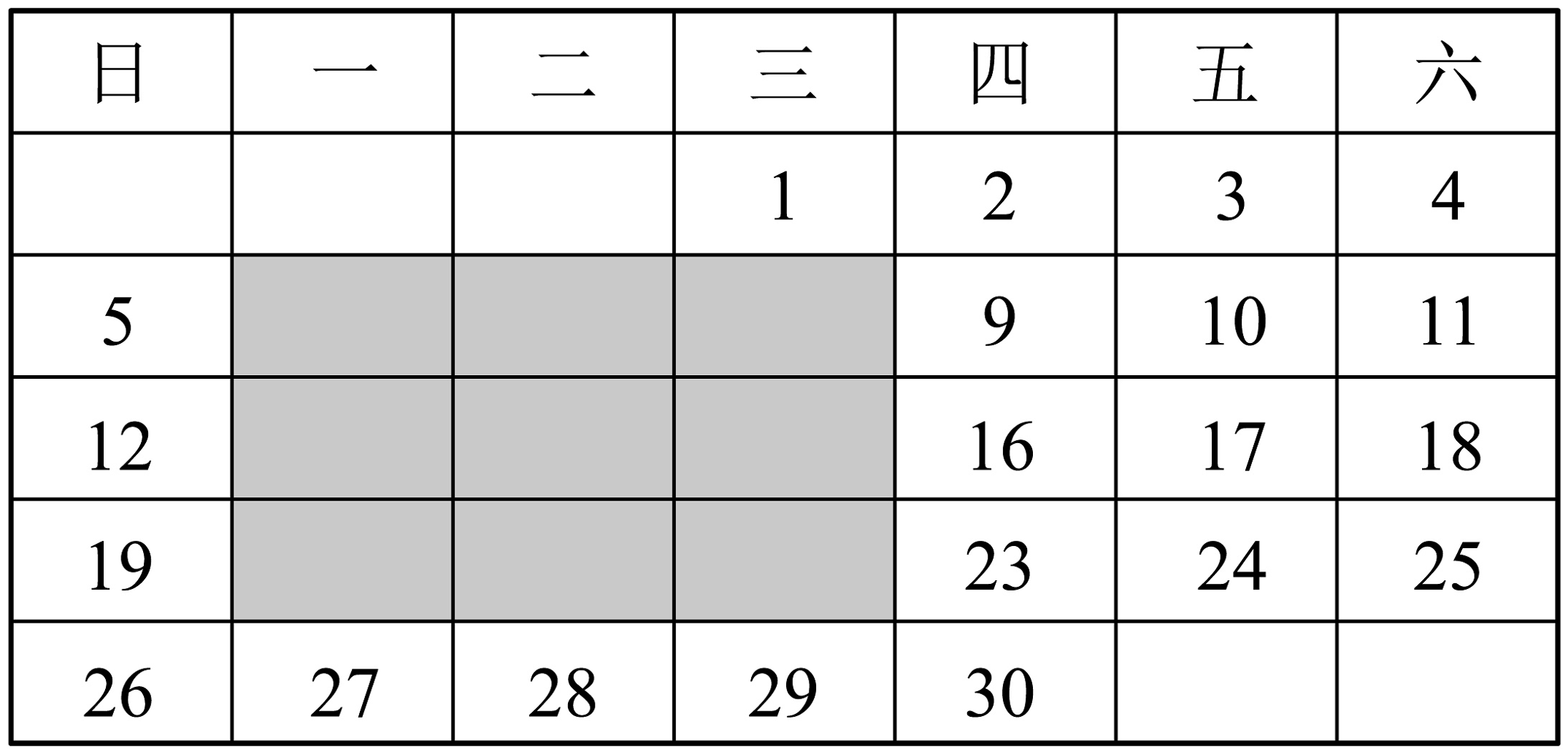(1)、九宫格中，四个角上的四个数之和与九宫格中央这个数有什么关系？(2)、请你自选一块九宫格进行计算，观察四个角上的四个数之和与九宫格中央那个数是否还有这种关系．（用虚线框圈出你所选定的九宫格）(3)、试说明原理． -
20、已知有理数 ， ， ， 满足 ， 求 ．