-
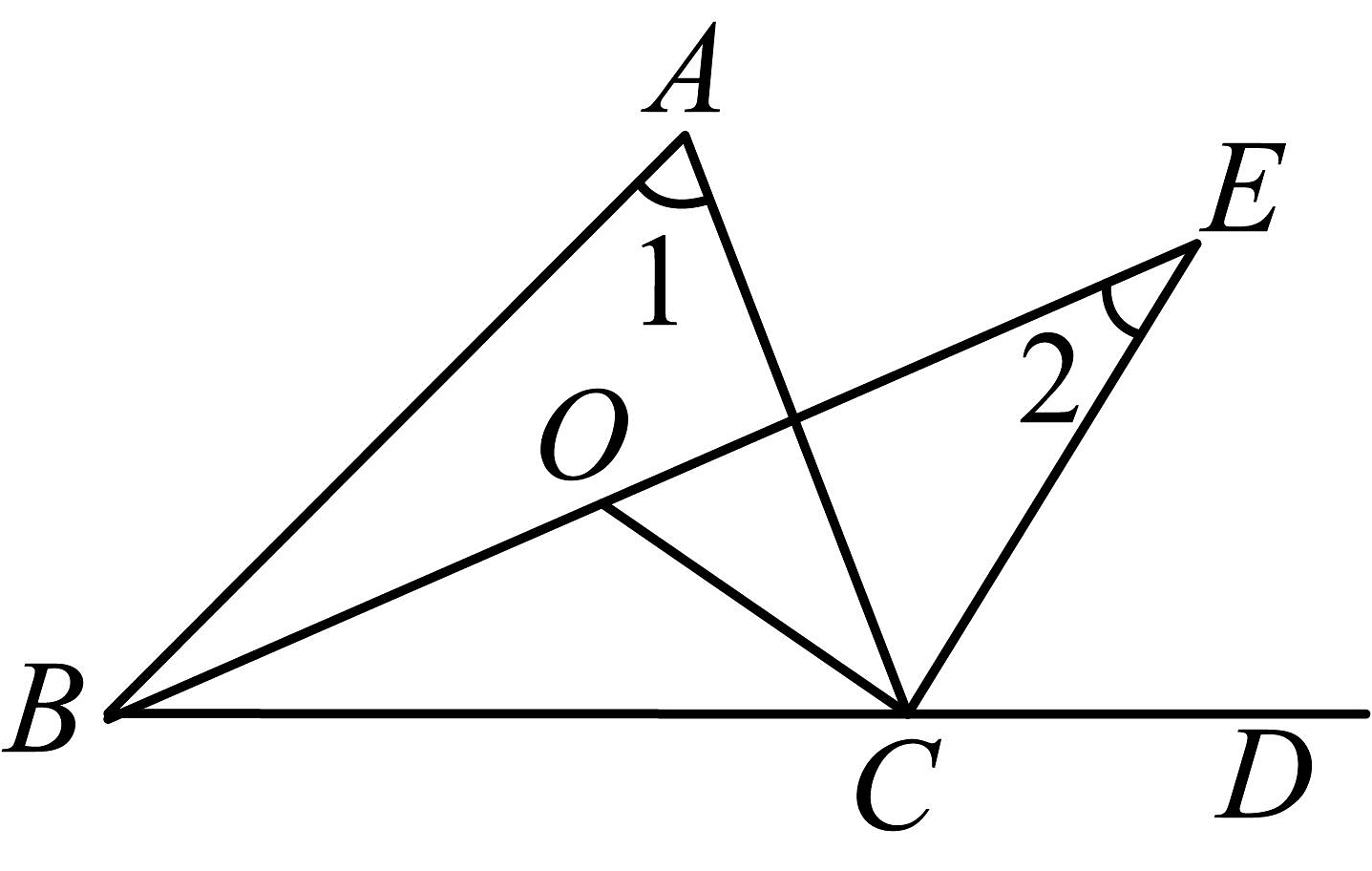
1、如图,在中, , 的平分线 , 交于点 , 为的外角的平分线,的延长线交于点 , , 则的大小为
-
2、如图,中, , 若沿图中虚线截去 , 则 .

-
3、 .
-
4、计算: .
-
5、若 , , 则( )A、150 B、160 C、165 D、180
-
6、下列各组长度的线段能构成三角形的是( )A、1,2,4 B、3,4,7 C、4,4,10 D、3,4,5
-
7、下列长度的两条线段与长度为12的线段首尾依次相连能组成直角形三角形的是( )A、6,9 B、9,15 C、10,16 D、15,18
-
8、9的算术平方根是( )A、 B、3 C、 D、81
-
9、已知,在四边形中, , , 分别是边上的点.且 . 探究线段的数量关系.
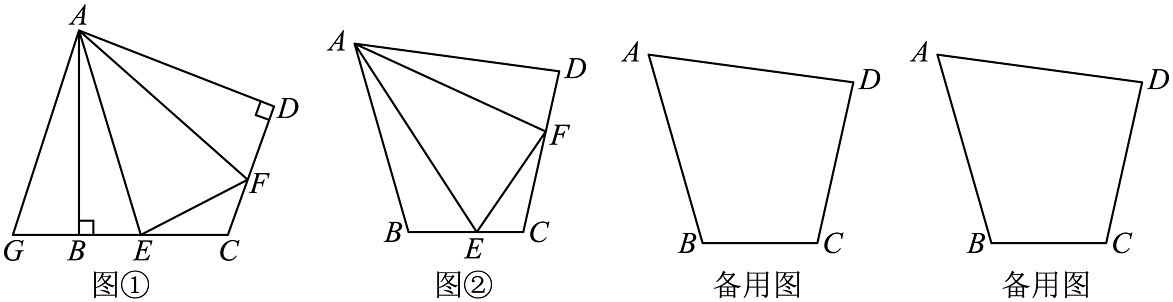 (1)、为探究上述问题,小宁先画出了其中一种特殊情况,如图①当 , 小宁探究此问题的方法是:延长到点 , 使 , 连接 , 请你补全小宁的解题思路:先证明________;再证明_________;即可得出线段之间的数量关系是______________________.(2)、如图②,在四边形中, , , 分别是边上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , 分别是所在直线上的点,且 . 请直接写出线段之间的数量关系.
(1)、为探究上述问题,小宁先画出了其中一种特殊情况,如图①当 , 小宁探究此问题的方法是:延长到点 , 使 , 连接 , 请你补全小宁的解题思路:先证明________;再证明_________;即可得出线段之间的数量关系是______________________.(2)、如图②,在四边形中, , , 分别是边上的点,且 , (1)中的结论是否仍然成立?请写出证明过程;(3)、在四边形中, , , 分别是所在直线上的点,且 . 请直接写出线段之间的数量关系. -
10、如图,在平面直角坐标系内,已知点 , 点 , 点 .
 (1)、画出关于y轴对称的;(2)、连结、 , 四边形的面积为______.
(1)、画出关于y轴对称的;(2)、连结、 , 四边形的面积为______. -
11、已知:如图,AC、DB相交于点O,AB=DC,∠ABO=∠DCO.
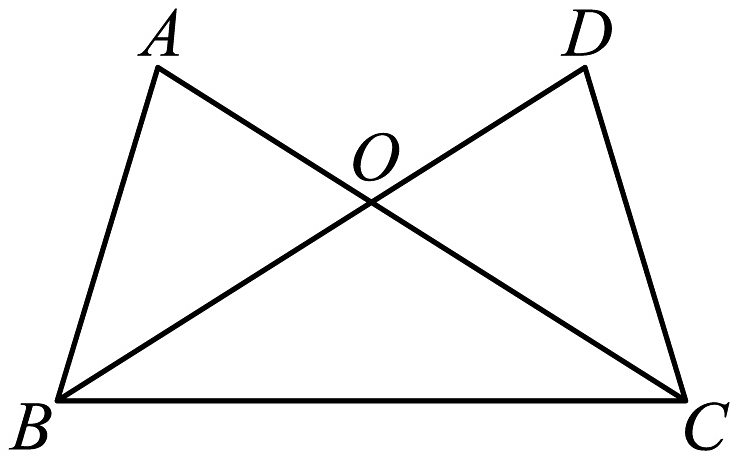
求证:(1)△ABO≌△DCO;
(2)若∠OBC=35°,求∠OCB的度数.
-
12、如图,分别是 , , 的中线,若 , 则 .

-
13、高速路上的路标警示牌,支撑结构采用三角形,是利用了三角形的 .
-
14、某酒店在客人退房后清洁客房需打扫卫生、整理床铺、更换客用物品、检查设备共四个步骤.某清洁小组有甲、乙、丙三名工作人员,工作要求如下:
①“打扫卫生”只能由甲完成;每间客房“打扫卫生”完成后,才能进行该客房的其他三个步骤,这三个步骤可由任意工作人员完成并可同时进行;
②一个步骤只能由一名工作人员完成,此步骤完成后该工作人员才能进行其他步骤;
③每个步骤所需时间如下表所示:
步骤
打扫卫生
整理床铺
更换客用物品
检查设备
所需时间/分钟
8
6
6
5
在不考虑其他因素的前提下,若由甲、乙、丙合作完成四间客房的清洁工作,则最少需要分钟.
-
15、先化简后求值: , 其中 .
-
16、如图,的面积是1,是的中线, , , 则的面积为 .

-
17、已知(m,n为正整数),则 .
-
18、计算: .
-
19、如图,在中, , 以A为圆心,任意长为半径画弧,分别交、于点M和点N,再分别以M、N为圆心,大于的长为半径画弧,两弧交于点P,连接并延长交于点D,下列结论:
①是的平分线;②;③分别连接、 , 则判定的依据是“”;④边上任意一点到边和边上的距离都相等;其中正确的结论共有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个 -
20、如图,已知 , , 于点C,于点G,若 , 则长度是_______.
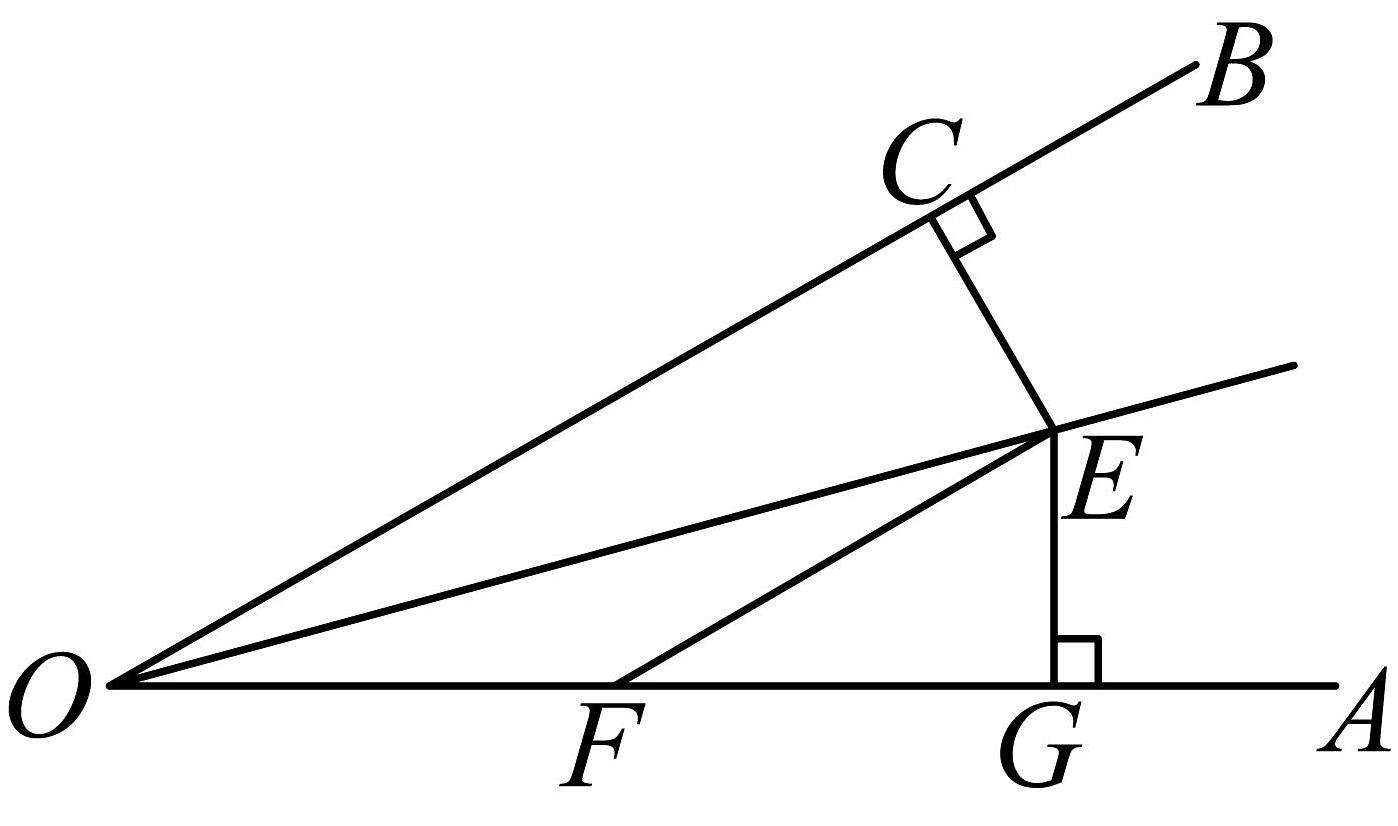 A、8 B、3 C、6 D、7
A、8 B、3 C、6 D、7