相关试卷

1、如图所示的点A，B，C，D，E中，哪两个点关于x轴对称?哪两个点关于y轴对称?点C 和点E 关于x轴对称吗?为什么?

查看解析
2、如图， D， E分别是AB， AC 的中点， CD⊥AB，垂足为D， BE⊥AC，垂足为E. 求证 AC=AB.

查看解析
3、下列各命题都成立，写出它们的逆命题.这些逆命题成立吗?

(1)、如果两个实数都是正数，那么它们的积是正数；

(2)、等边三角形是锐角三角形；

(3)、如果两个角是直角，那么它们相等；

(4)、角的内部到角的两边距离相等的点在角的平分线上.

查看解析
4、下列图形是轴对称图形吗?如果是，画出它们的对称轴.

查看解析
5、已知数轴上A、B两点表示的数分别为a，b，且a，b满足|a+20|+(b-13)²=0，点C表示的数为16，点D表示的数为-7．
（1）A，C两点之间的距离为__________；
（2）已知|m－n|可理解为数轴上表示数m、n的两点之间的距离．
若点P在数轴上表示的数为x，则满足|x+2|+|x-3|=5的所有的整数x的和为_______________；满足|x+2|+|x-3|=9的x值为______________．
（3）点A，B从起始位置同时出发相向匀速运动，点A的速度为6个单位长度/秒，点B的速度为2个单位长度/秒，当点A运动到点C时，迅速以原来的速度返回，到达出发点后，又折返向点C运动，点B运动至点D后停止运动，当点B停止运动时，点A也停止运动，求在此运动过程中，求A，B两点同时到达的点在数轴上表示的数．

查看解析
6、先化简，再求值：已知 $a = 2$ ， $b = - 1$ ，求 $5 a b^{2} - 2 [a^{2} b - 2 (2 a b^{2} - a^{2} b)]$ 的值．

查看解析
7、问题：10袋小麦称后记录（单位： $kg$ ）如图所示，10袋小麦平均每袋多少千克？
经过分析，某小组同学们的思路是：以 $50 kg$ 为标准，超过的记为正数，不足的记为负数，求出这10个数的平均数后再加50．

查看解析
8、下列各组数中，互为相反数的一组是（）

A、 $3^{2}$ 和 ${(- 3)}^{2}$ B、 $3^{2}$ 和 $2^{3}$ C、 $- 2^{3}$ 和 ${(- 2)}^{3}$ D、 $- 2^{4}$ 和 $4^{2}$

查看解析
9、下列各组单项式中，是同类项的是（）

A、 $a^{3}$ 与 $b^{3}$ B、 $2 a$ 与 $2 b$ C、 $- \frac{1}{3} a^{2} b^{3}$ 与 $5 a^{3} b^{2}$ D、 $3 a$ 与 $- a$

查看解析
10、点A，B，C为数轴上的三点，如果点C在点A，B之间，且到点A的距离是点C到点B的距离的3倍，那么我们就称点C是{A，B}的奇妙点．例如，如图①，点A表示的数为－3，点B表示的数为1.表示0的点C到点A的距离是3，到点B的距离是1，那么点C是{A，B}的奇妙点；又如，表示－2的点D到点A的距离是1，到点B的距离是3，那么点D就不是{A，B}的奇点，但点D是{B，A}的奇妙点．
【知识运用】
如图②，M，N为数轴上的两点，点M所表示的数为－2，点N所表示的数为6.
(1)表示数_____的点是{M，N}的奇妙点；表示数______的点是{N，M}的奇妙点；
(2)若点P所表示的数为3，点P是{M，N}的奇妙点，则点M、N所表示的数可以是几？M=______，N=_____(写出一组即可)
(3)如图③，A，B为数轴上的两点，点A所表示的数为－10，点B所表示的数为50.现有一动点P从点A出发向右运动，点P运动到数轴上的什么位置时，P，A，B中恰有一个点为其余两点的奇妙点？

查看解析
11、有这样一道题“如果式子 $5 a + 3 b$ 的值为 $- 4$ ，那么式子 $2 (a + b) + 4 (2 a + b)$ 的值是多少？”爱动脑筋的佳佳同学这样来解：原式 $= 2 a + 2 b + 8 a + 4 b = 10 a + 6 b$ ．我们把 $5 a + 3 b$ 看成一个整体，则原式 $= 2 (5 a + 3 b) = 2 \times (- 4) = - 8$ ．
整体思想是中学数学解题中的一种重要思想方法，它在多项式的化简与求值中应用极为广泛，仿照佳佳的解题方法，完成下面问题：

(1)、已知 $a^{2} - 2 a = 1$ ，则 $2 a^{2} - 4 a + 1 =$ ______；

(2)、已知 $m + n = 2$ ， $m n = - 4$ ，求 $2 (m n - 3 m) - 3 (2 n - m n)$ 的值；

(3)、已知 $a - 2 b = 2$ ， $2 b - c = - 5$ ， $c - d = 9$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值．

查看解析
12、如图所示，宽为20米，长为32米的长方形地面上，修筑宽度为x米的两条互相垂直的小路，余下的部分作为耕地，如果要在耕地上铺上草皮，选用草皮的价格是每平米a元，
（1）求买草皮至少需要多少元？（用含a，x的式子表示）
（2）计算a＝40，x＝2时，草皮的费用．

查看解析
13、计算：

(1)、 $(\frac{1}{4} - \frac{2}{3} + \frac{1}{6}) \div (- \frac{1}{12})$ ；

(2)、 $- 1^{4} - (1 - 0.5) \times \frac{1}{3} \times |3 - {(- 3)}^{2}|$ ．

查看解析
14、画出数轴，在数轴上表示下列各数，并用“>”连接：0， $- 5 ，$ $- |- 2.5|$ ， $1 \frac{1}{2}$ ， $- (- 4)$ ， $- \frac{1}{3}$ ．

查看解析
15、生物学中，描述、解释和预测种群数量的变化，常常需要建立数学模型．在营养和生存空间没有限制的情况下，某种细胞可通过分裂来繁殖后代，我们就用数学模型 $2^{n}$ 来表示，即： $2^{1} = 2$ ， $2^{2} = 4$ ， $2^{3} = 8$ ， $2^{4} = 16$ ， $2^{5} = 32$ ， …，请你推算 $2^{1} + 2^{2} + 2^{3} + 2^{4} + 2^{5} + \cdot \cdot \cdot + 2^{2023}$ 的个位数字是

查看解析
16、按如图所示的运算程序，若输入 $m = - 2, n = - 3$ ，则输出y的值为．

查看解析
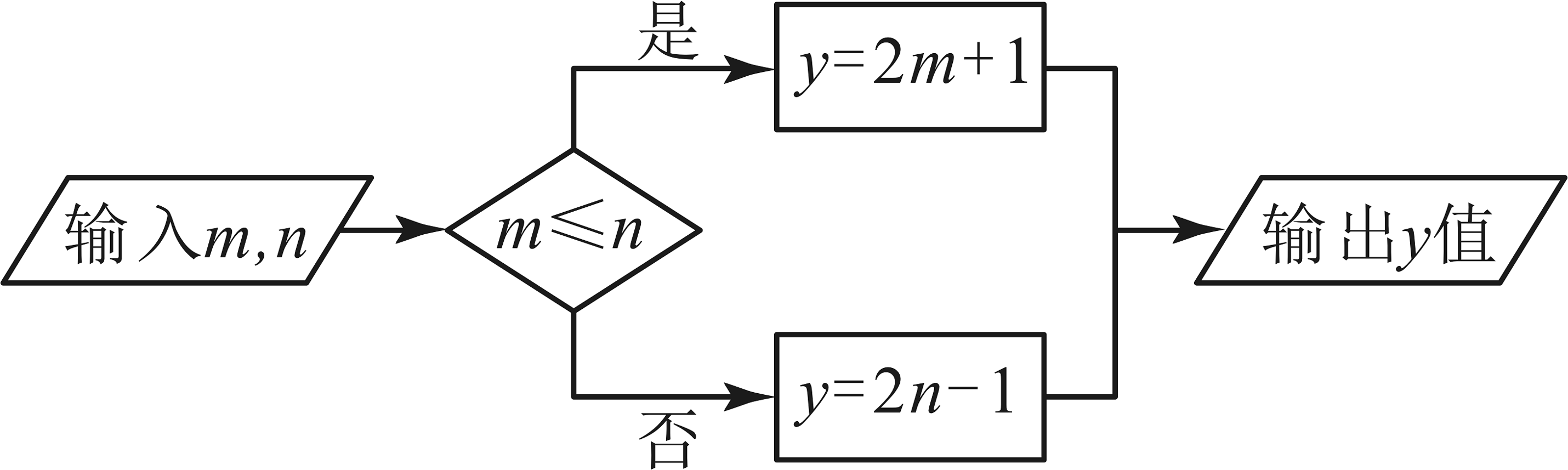
17、已知a，b两数在数轴上的位置如图所示，则化简代数式 $|a + b| - |a - 1| + |b + 2| =$ ．

查看解析
18、若 $5 x^{2 m + 1} y^{2}$ 与 $- 7 x^{5} y^{3 n - 1}$ 是同类项，则 $m =$ ， $n =$ ．

查看解析
19、已知 $(m - 1) x^{|m|} - 3 = 0$ 是关于 $x$ 的一元一次方程，则 $m$ 的值为．

查看解析
20、规定，是一种新的运算符号，且 $a ▲ b = a b + a + b$ ，例如： $2 ▲ 3 = 2 \times 3 + 2 + 3 = 11$ ，那么 $(3 ▲ 4) ▲ 1 =$ （）

A、19 B、29 C、39 D、49

查看解析

上一页 151 152 153 154 155 下一页跳转