浙教版数学八年级上学期重难点复习3：轴对称的应用
试卷更新日期：2025-09-12 类型：复习试卷
一、镜面对称
-
1. 当写有数字的纸条垂直于镜面摆放时(如图所示）：
下面是从镜子中看到的一串数
，它其实是.2. 镜中像 站在一个平面镜面前，大家总能看到自己的像.如果你站在两个有夹角的平面镜前，通常镜子中能看到不止两个你的像.那么当两个平面镜的夹角为60°时，共可以呈现个你的像.3. 如图，等腰是由三块面向内的镜面组成的，其中 ， 边上靠近点的三等分点处发出一道光线 ， 经镜面两次反射后恰好回到点 ， 若 ， 则光线走过的路径是 ．
4. 阅读下列材料并完成任务：“最短路径问题”是数学中一类具有挑战性的问题．其实，数学史上也有不少相关的故事，如下即为其中较为经典的一则：古希腊有一位久负盛名的学者，名叫海伦．他精通数学，物理，聪慧过人．有一天，一位将军向他请教一个问题：如图1，将军从甲地骑马出发，要到河边让马饮水，然后再回到乙地的马棚，为使马走的路程最短，应该让马在什么地方饮水？海伦认为以河边为镜面，画出甲地的镜像点(垂直河边的等距离点)，然后连接乙地和甲地的镜像点，会跟河边相交一点，这个点就是马饮水的地方，马走的路程最短(两点之间直线距离最短)．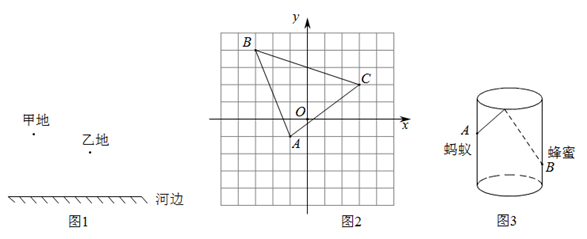
任务：
(1)、请你帮海伦在图1的位置完成作图，并标出马饮水的地点P（画出草图即可）；(2)、如图2， ABC的三个顶点的坐标分别为A(-1，-1)，B(-3，4)，C(3，2)．请你在x轴上找一点Q ， 使得QB+QC最小（保留作图痕迹）；(3)、应用：如图3，圆柱形容器高为18cm，底面周长为24cm．在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm处的点A处，点A与B的水平距离等干底面直径，求蚂蚁从外壁A处到达内壁B处的最短距离．
二、光的反射
-
5. 如图，两面镜子的夹角为 ， 当光线经过镜子反射时，入射角等于反射角，即 ， ． 若 ， ， 则的度数为（ ）
A、 B、 C、 D、6. 如图，在中， ， 从点射出的光线经过、反射恰好回到点，根据光的反射性质，有 ， ， 连结 ． 若 ， 以下结论正确的是（ ）
① ， ② ， ③ ， ④平分 ．
A、①②④ B、①③④ C、①②③ D、②③④7. 如图1，六分仪是一种测量天体高度的航海仪器，观测者手持六分仪，可得出观测点的地理坐标．在图2所示的“六分仪原理图”中，所观测星体记为S，两个反射镜面位于A，B两处，B处的镜面所在直线自动与刻度线保持平行（即），并与A处的镜面所在直线相交于点C，所在直线与水平线相交于点D， ， 观测角=（用表示）．
小贴士：
如图3，光线经过镜面反射时，反射角等于入射角，所以图2中 ，
三、台球桌上的轴对称
-
8. 如图为台球桌示意图，已知台球桌边框AB与BC垂直，球杆沿着直线m击打白球后，经过两次撞击后沿着直线n运动，已知∠ADF=46°，则∠GEC的度数为 ( )
A、47° B、46° C、45° D、44°9. 台球技艺中包含了许多物理、数学的知识．图1是台球桌面的一部分，由于障碍球E的阻挡，击球者想通过正面击打主球M，使其撞击台球桌边框（仅碰撞一次），经过一次反弹后正面撞击到目标球F．球的反弹路径类似于光的反射光路．台球桌面抽象为长方形，球抽象为点，如图2，请在边上作出撞击点P，使得 ， 并用数学知识进行证明．
锦囊：某同学阅读理解题意后，先画了一个草图（如图3）进行分析，发现“要保证 ， 只需保证即可”．
10. 操作题：台球桌的形状是一个长方形，当母球被击打后可能在不同的边上反弹，为了使母球最终击中目标球，击球者需作出不同的设计，确定击球方向．如图，目标球从A点出发经B点到C点，相当于从点出发直接击打目标球C，其实质上是图形的轴对称变换，关键是找母球关于桌边的对称点的位置．
(1)、如下图，小球起始时位于点处，沿所示的方向击球，小球运动的轨迹如图所示．如果小球起始时位于点处，仍按原来方向击球，那么在点A，B，C，D，E，F，G，H中，小球会击中的点是___________；
(2)、在下图中，请你设计一条路径，使得球P依次撞击台球桌边AB，BC反射后，撞到球Q．（不写作法，保留作图痕迹．）
四、折叠问题
-
11. 如图，将沿折叠得到 ， 再将沿折叠得到 ， 连接 ， 交于点 ， 连接 ， 与相交于点 ， 若 ， 则的度数为（ ）
A、 B、 C、 D、12. 如图，在△ABC中，∠ACB＝90°，首先沿着CD折叠，点B落在点E处，然后沿着FG折叠，使得点A与点E重合，则下列说法中（ ）①EF⊥CE；②若BC＝3，AC＝4，那么 ．
A、①正确，②正确 B、①正确，②错误 C、①错误，②正确 D、①错误，②错误
