沪科版数学九年级上册二次函数重难点题型梳理
试卷更新日期:2025-09-12 类型:复习试卷
一、二次函数与系数关系
-
1. 如图,抛物线的对称轴是 . 下列结论:①;②;③;④ , 正确的有( )
 A、4个 B、3个 C、2个 D、1个2. 二次函数的图象如图所示,下列结论:①;②;③m为任意实数,则;④;⑤若 , 且 , 则 . 其中正确的个数是( )
A、4个 B、3个 C、2个 D、1个2. 二次函数的图象如图所示,下列结论:①;②;③m为任意实数,则;④;⑤若 , 且 , 则 . 其中正确的个数是( ) A、2个 B、3个 C、4个 D、5个3. 已知二次函数为常数, , 当时, , 则二次函数的图象可能为( )A、
A、2个 B、3个 C、4个 D、5个3. 已知二次函数为常数, , 当时, , 则二次函数的图象可能为( )A、 B、
B、 C、
C、 D、
D、
二、二次函数与一元二次方程的关系
-
4. 已知二次函数的图像过点 , 对称轴为直线 . 下列四个结论:①;②若点 , 均在该二次函数图象上,则;③若m为任意实数,则;④对于任何实数k,关于x的方程必有两个不相等的实数根,其中正确的( )A、①②③ B、①②④ C、①③④ D、②③④5. 如图,二次函数的图像与x轴交于两点 , , 且.下列结论:
①;②;③;④若m和n是关于x的一元二次方程)的两根,且 , 则 , ;⑤关于x的不等式)的解集为.其中正确结论的个数是( )
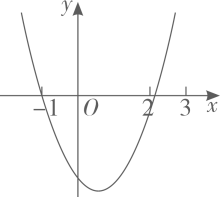 A、2 B、3 C、4 D、56. 如图,已知抛物线(为常数,且)的对称轴是直线 , 且抛物线与轴的一个交点坐标是 , 与轴交点坐标是且 . 有下列结论:①;②;③;④关于的一元二次方程必有两个不相等实根;⑤若点在抛物线上,
A、2 B、3 C、4 D、56. 如图,已知抛物线(为常数,且)的对称轴是直线 , 且抛物线与轴的一个交点坐标是 , 与轴交点坐标是且 . 有下列结论:①;②;③;④关于的一元二次方程必有两个不相等实根;⑤若点在抛物线上,且 , 当时,则的取值范围为 .

其中正确的有( )
A、2个 B、3个 C、4个 D、5个三、二次函数与解不等式
-
7. 已知二次函数(b , c为常数),(1)、若抛物线与x轴正半轴的交点坐标是(1,0),对称轴为直线 , 求抛物线的解析式;(2)、若 , 设函数图象的顶点坐标为 , 当b的值变化时,求m与n的关系式;(3)、已知二次函数图象经过两点,若时,总有 , 求q-p的取值范围.8. 都是实数,且 ,则 之间的大小关系是 ( )A、 B、 C、 D、9. 在二次函数中,(1)、若它的图象过点 , 则t的值为多少?(2)、当时,y的最小值为 , 求出t的值:(3)、如果都在这个二次函数的图象上,且 , 求m的取值范围.
四、构造二次函数解决最值问题
-
10. 如图,在平面直角坐标系中 , 与轴交于两点(A在的左侧),与轴交于点 , 点是上方抛物线上一点,连结交于点 , 连结 , 记的面积为 , 的面积为 , 则的最大值为( )
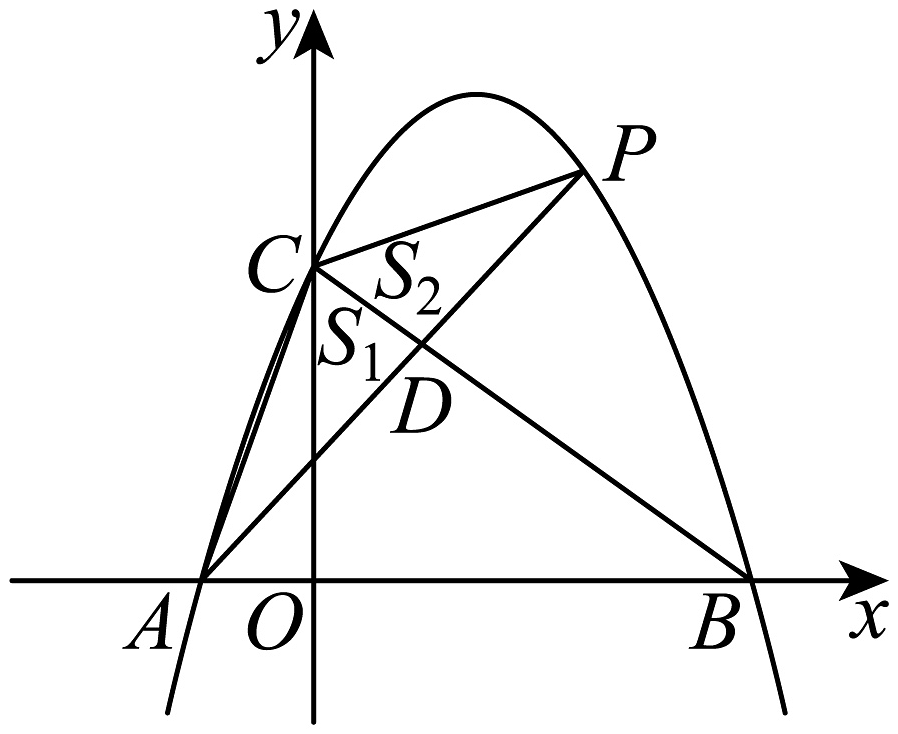 A、 B、 C、 D、1
A、 B、 C、 D、1五、二次函数的新定义问题
-
11. 对于一个函数,当自变量取时,函数值也等于 , 则称是这个函数的不动点.已知二次函数 .
(1)若2是此函数的不动点,则的值为 .
(2)若此函数有两个相异不动点与 , 且 , 则的取值范围是 .
12. 若一个点的纵坐标是横坐标的2倍,则称这个点为“二倍点”,如: , , 等都是“二倍点”.在的范围内,若二次函数的图像上至少存在一个“二倍点”,则的取值范围是 .13. 在平面直角坐标系中,设二次函数(a,b是常数,).(1)、若时,图象经过点 , 求二次函数的表达式.(2)、写出一组a,b的值,使函数的图象与x轴只有一个公共点,并求此二次函数的顶点坐标.(3)、已知,二次函数的图象和直线都经过点 , 求证: .14. 在平面直角坐标系中,抛物线的顶点为P,且该抛物线与x轴交于A,B两点(点A在点B的左侧).我们规定;抛物线与x轴围成的封闭区域称为“G区城”(不包含边界),横、纵坐标都是整数的点称为整点.(1)、求抛物线的顶点P的坐标(用含a的代数式表示);(2)、如果抛物线经过(1,3).①求a的值
②在①的条件下,直接写出“G区域”内整点的坐标;
(3)、如果抛物线在“G区域”内有4个整点,求a的取值范围,六、二次函数的应用(抛物线形问题)
-
15. 2023年第十九届亚运会在杭州举行,这是我国第三次举办亚运会,在中国队对阵韩国队的男篮四分之一决赛中,中国队表现出色,赢得了比赛.如图,一名中国运动员在距离篮球框中心A点4(水平距离)远处跳起投篮,篮球准确落入篮框,已知篮球运行的路线为抛物线,当篮球运行水平距离为2.5时,篮球达到最大高度B点处,且最大高度为3.5 , 以地面水平线为x轴,过最高点B垂直地面的直线为y轴建立平面直角坐标系,如果篮框中心A距离地面3.05 , 那么篮球在该运动员出手时的高度是多少米?
 16. 排球场的长度为 , 球网在场地中央且高度为 . 排球出手后的运动路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,排球运动过程中的竖直高度(单位:)与水平距离(单位:) 近似满足函数关系 .
16. 排球场的长度为 , 球网在场地中央且高度为 . 排球出手后的运动路线可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,排球运动过程中的竖直高度(单位:)与水平距离(单位:) 近似满足函数关系 . (1)、某运动员第一次发球时,测得水平距离与竖直高度的几组数据如下:
(1)、某运动员第一次发球时,测得水平距离与竖直高度的几组数据如下:水平距离
竖直高度
①根据上述数据,求这些数据满足的函数关系;
②判断该运动员第一次发球能否过网,并说明理由.
(2)、该运动员第二次发球时,排球运动过程中的竖直高度(单位:) 与水平距离(单位:) 近似满足函数关系 , 请问该运动员此次发球是否出界,并说明理由.七、二次函的数应用(利润问题)
-
17. 2024年“五一”假期期间,阆中古城景区某特产店销售A,B两类特产.A类特产进价50元/件,B类特产进价60元/件.已知购买1件A类特产和1件B类特产需132元,购买3件A类特产和5件B类特产需540元.(1)、求A类特产和B类特产每件的售价各是多少元?(2)、A类特产供货充足,按原价销售每天可售出60件.市场调查反映,若每降价1元,每天可多售出10件(每件售价不低于进价).设每件A类特产降价x元,每天的销售量为y件,求y与x的函数关系式,并写出自变量x的取值范围.(3)、在(2)的条件下,由于B类特产供货紧张,每天只能购进100件且能按原价售完.设该店每天销售这两类特产的总利润为w元,求w与x的函数关系式,并求出每件A类特产降价多少元时总利润w最大,最大利润是多少元?(利润=售价-进价)18. 为了振兴乡村经济,增加村民收入,某村委会干部带领村民把一片坡地改造后种植了优质葡萄,今年正式上市销售,并在网上直播推销优质葡萄.在销售的30天中,第一天卖出20千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出4千克.第天的售价为y元/千克,y关于x的函数解析式为且第12天的售价为32元/千克,第26天的售价为25元/千克.已知种植销售葡萄的成本是18元/千克,每天的利润是元.(1)、 , ;(2)、销售优质葡萄第几天时,当天的利润最大?最大利润是多少?19. 某经销商到“幸福村”蔬菜种植基地定点采购甲种蔬菜,已知甲种蔬菜的单价(元千克)与采购量(千克)之间的函数关系如图中折线所示(不包括端点).
 (1)、当时,直接写出与之间的函数解析式;(2)、若甲种蔬菜的种植成本为元/千克,采购量不超过千克,那么当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?(3)、在(2)的条件下,求采购甲种蔬菜多少千克时,蔬菜种植基地能获利元?20. 近段时间,位于汇川区泗渡镇泗渡农场的125亩草莓迎来了冬季采摘期,该农场以优良的生态环境为基础,采用蜜蜂自然授粉的方式,提升草莓的产量和品质使得草莓香甜可口,果实饱满,吸引了不少游客前往采摘.请阅读以下材料,帮助农户解决问题.
(1)、当时,直接写出与之间的函数解析式;(2)、若甲种蔬菜的种植成本为元/千克,采购量不超过千克,那么当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?(3)、在(2)的条件下,求采购甲种蔬菜多少千克时,蔬菜种植基地能获利元?20. 近段时间,位于汇川区泗渡镇泗渡农场的125亩草莓迎来了冬季采摘期,该农场以优良的生态环境为基础,采用蜜蜂自然授粉的方式,提升草莓的产量和品质使得草莓香甜可口,果实饱满,吸引了不少游客前往采摘.请阅读以下材料,帮助农户解决问题.
材料1:某农户承包了一块矩形土地,建立了三个草莓种植大棚,其布局如图所示,其中米,米,阴影部分规划为大棚种植草莓,其余部分是等宽的通道.
材料2:当售价为60元时,每天可销售40 , 该农户调查发现,决定降价销售,若销售单价每降低1元,每天可多销售2千克.已知每千克草莓的成本为20元.
(1)、若三个大棚的面积是1400 , 求道路的宽度;(2)、当售价定为多少元时,利润最大?并求出最大利润.八、二次函数的应用(存在性问题)
-
21. 如图所示,已知抛物线y=ax2+bx+c(a≠0)经过点A(﹣2,0)、B(4,0)、C(0,﹣8),与直线y=x﹣4交于B,D两点
(1)求抛物线的解析式并直接写出D点的坐标;
(2)点P为直线BD下方抛物线上的一个动点,试求出△BDP面积的最大值及此时点P的坐标;
(3)点Q是线段BD上异于B、D的动点,过点Q作QF⊥x轴于点F,交抛物线于点G,当△QDG为直角三角形时,直接写出点Q的坐标.
 22. 如图,抛物线经过 , 两点,并且与轴交于点 .
22. 如图,抛物线经过 , 两点,并且与轴交于点 . (1)、求此抛物线的解析式;(2)、直接写出直线的解析式为;(3)、若点是第一象限的抛物线上的点,且横坐标为 , 过点作轴的垂线交于点 , 设的长为 , 求与之间的函数关系式及的最大值;(4)、在轴的负半轴上是否存在点 , 使以 , , 三点为顶点的三角形为等腰三角形?如果存在,直接写出点的坐标;如果不存在,说明理由.23. 如图,在平面直角坐标系中,抛物线( , 是常数)经过点 , 点 . 点在此抛物线上,其横坐标为 .
(1)、求此抛物线的解析式;(2)、直接写出直线的解析式为;(3)、若点是第一象限的抛物线上的点,且横坐标为 , 过点作轴的垂线交于点 , 设的长为 , 求与之间的函数关系式及的最大值;(4)、在轴的负半轴上是否存在点 , 使以 , , 三点为顶点的三角形为等腰三角形?如果存在,直接写出点的坐标;如果不存在,说明理由.23. 如图,在平面直角坐标系中,抛物线( , 是常数)经过点 , 点 . 点在此抛物线上,其横坐标为 . (1)、求此抛物线的解析式;(2)、当点在轴上方时,结合图象,直接写出的取值范围;(3)、若此抛物线在点左侧部分(包括点)的最低点的纵坐标为 .
(1)、求此抛物线的解析式;(2)、当点在轴上方时,结合图象,直接写出的取值范围;(3)、若此抛物线在点左侧部分(包括点)的最低点的纵坐标为 .①求的值;
②以为边作等腰直角三角形 , 当点在此抛物线的对称轴上时,直接写出点的坐标.
24. 如图,抛物线与轴交于、两点(点在点的左侧),点的坐标为 , 与轴交于点 , 作直线 . 动点在轴上运动,过点作轴,交抛物线于点 , 交直线于点 , 设点的横坐标为 .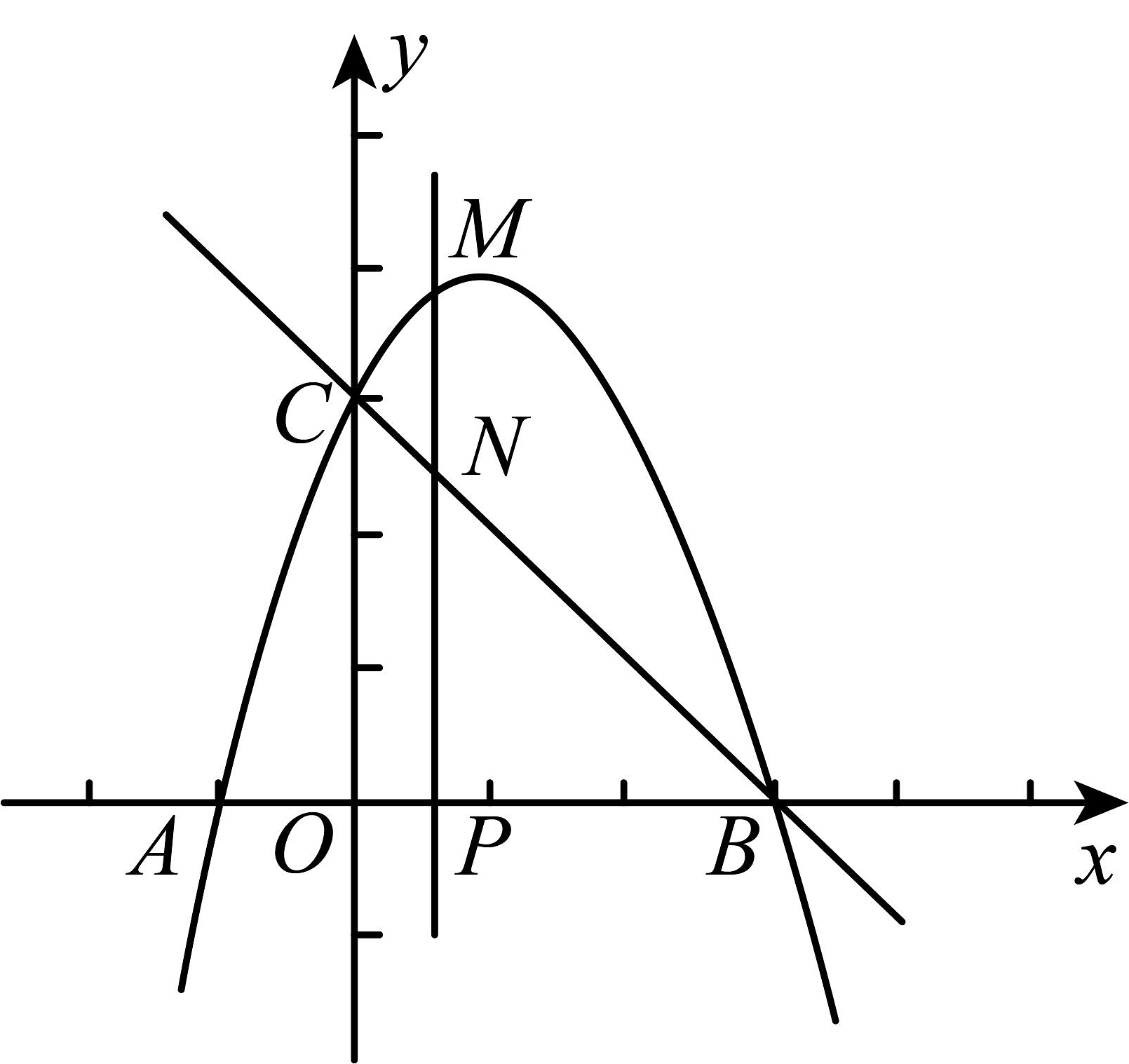 (1)、求抛物线的解析式和直线的解析式;(2)、当点在线段上运动时,求线段的最大值;(3)、当点在线段上运动时,若是以为腰的等腰直角三角形时,求的值;(4)、当以、、、为顶点的四边形是平行四边形时,直接写出的值.25. 如图,抛物线与轴交于点和点 , 与轴交于点 , 点在抛物线上.
(1)、求抛物线的解析式和直线的解析式;(2)、当点在线段上运动时,求线段的最大值;(3)、当点在线段上运动时,若是以为腰的等腰直角三角形时,求的值;(4)、当以、、、为顶点的四边形是平行四边形时,直接写出的值.25. 如图,抛物线与轴交于点和点 , 与轴交于点 , 点在抛物线上. (1)、求抛物线的解析式;(2)、点在第一象限内,过点作轴,交于点 , 作轴,交抛物线于点 , 点在点的左侧,以线段为邻边作矩形 , 当矩形的周长为11时,求线段的长;(3)、点在直线上,点在平面内,当四边形是正方形时,请直接写出点的坐标.26. 如图,抛物线交x轴于点和点 , 交y轴于点C.
(1)、求抛物线的解析式;(2)、点在第一象限内,过点作轴,交于点 , 作轴,交抛物线于点 , 点在点的左侧,以线段为邻边作矩形 , 当矩形的周长为11时,求线段的长;(3)、点在直线上,点在平面内,当四边形是正方形时,请直接写出点的坐标.26. 如图,抛物线交x轴于点和点 , 交y轴于点C. (1)、求抛物线的表达式;(2)、若点P是直线下方抛物线上一动点,连接 , 当的面积最大时,求点P的坐标及面积的最大值;(3)、在(2)的条件下,若点N是直线上的动点,在平面内的是否存在点Q,使得以为边、以P、B、N、Q为顶点的四边形是菱形?若存在,请求出符合条件的所有Q点的坐标:若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、若点P是直线下方抛物线上一动点,连接 , 当的面积最大时,求点P的坐标及面积的最大值;(3)、在(2)的条件下,若点N是直线上的动点,在平面内的是否存在点Q,使得以为边、以P、B、N、Q为顶点的四边形是菱形?若存在,请求出符合条件的所有Q点的坐标:若不存在,请说明理由.九、二次函数的应用(面积问题)
-
27. 如图,已知抛物线与轴交于点 , 与轴交于两点,点在点左侧.点的坐标为 , 点的坐标为 .
 (1)、求抛物线的解析式;(2)、当点是抛物线对称轴上的一个动点时,求当最小时,点的坐标;(3)、若点是线段下方抛物线上的动点,求面积的最大值.28. 直线yx+c与x轴交于点A(3,0),与y轴交于点B,抛物线yx2+bx+c经过点A,B.M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.
(1)、求抛物线的解析式;(2)、当点是抛物线对称轴上的一个动点时,求当最小时,点的坐标;(3)、若点是线段下方抛物线上的动点,求面积的最大值.28. 直线yx+c与x轴交于点A(3,0),与y轴交于点B,抛物线yx2+bx+c经过点A,B.M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N. (1)、求点B的坐标;(2)、求抛物线的解析式;(3)、点M在线段OA上运动,
(1)、求点B的坐标;(2)、求抛物线的解析式;(3)、点M在线段OA上运动,①求线段PN的最大长度.
②连接AN,求△ABN面积的最大值.
29. 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开(如图1所示).已知计划中的材料可建墙体总长46米,设两间饲养室合计长(米),总占地面积为. (1)、求关于的函数表达式和自变量的取值范围.(2)、现需要设计这两间饲养室各开一扇门(如图2所示),每扇门宽1米,门不采用计划中的材料.求总占地面积最大为多少?30. 为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长)和长的篱笆墙,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆墙,且不浪费篱笆墙),请根据设计方案回答下列问题:
(1)、求关于的函数表达式和自变量的取值范围.(2)、现需要设计这两间饲养室各开一扇门(如图2所示),每扇门宽1米,门不采用计划中的材料.求总占地面积最大为多少?30. 为落实国家《关于全面加强新时代大中小学劳动教育的意见》,某校准备在校园里利用围墙(墙长)和长的篱笆墙,围成Ⅰ、Ⅱ两块矩形劳动实践基地.某数学兴趣小组设计了两种方案(除围墙外,实线部分为篱笆墙,且不浪费篱笆墙),请根据设计方案回答下列问题: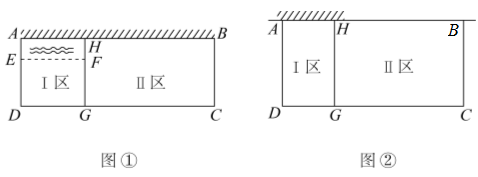 (1)、方案一:如图①,全部利用围墙的长度,但要在Ⅰ区中留一个宽度的水池且需保证总种植面积为 , 试分别确定、的长;(2)、方案二:如图②,使围成的两块矩形总种植面积最大,请问应设计为多长?此时最大面积为多少?31. 有这样一个例题:有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为 , 如何设计这个窗户,使透光面积最大?
(1)、方案一:如图①,全部利用围墙的长度,但要在Ⅰ区中留一个宽度的水池且需保证总种植面积为 , 试分别确定、的长;(2)、方案二:如图②,使围成的两块矩形总种植面积最大,请问应设计为多长?此时最大面积为多少?31. 有这样一个例题:有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为 , 如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为时,透光面积最大值约为 . 我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为 , 利用图3,解答下列问题:
(1)、若为 , 求此时窗户的透光面积?(2)、与上一个例题比较,改变窗户形状后,若设的长度为 , 请问当x的值为多少时窗户透光面积最大?与例题相比透光的最大面积是否变大?通过计算说明.十、二次函数的应用(增减性问题)
-
32. 已知二次函数 ( 为常数)的图象经过点 ,对称轴是直线 。
(1)、求此二次函数的表达式。(2)、求二次函数 的最大值。(3)、当 时,二次函数 的最大值与最小值的差为 ,求 的取值范围。
-