第四章《相交线和平行线》提升卷—华东师大版数学七(上)单元测
试卷更新日期:2025-09-13 类型:单元试卷
一、选择题:本大题共10小题,每小题3分,共30分
-
1. 如图,直线AB,CD 相交于点O,OE⊥AB 于点O,OF 平分∠AOE,∠1=15°31' , 则下列结论中不正确的是( ).
 A、 B、∠1=∠3 C、∠AOD与∠1互为补角 D、∠1的余角等于 75°31'2. 下列语句中,正确的是( )A、相等的角一定为对顶角 B、不是对顶角的角一定不相等 C、不相等的角一定不是对顶角 D、有公共顶点且和为的两个角一定为邻补角3. 已知A、B、C三点,若过其中任意两点画一条直线,则画出的不同直线( )A、一定有三条 B、只能有一条 C、可能有三条,也可能只有一条 D、以上结论都不对4. 如果同一平面内有三条直线,那么它们交点个数是( )个.A、3个 B、1或3个 C、1或2或3个 D、0或1或2或3个5. 若平面内互不重合的4条直线只有3个交点,则平面被分成了( )个部分.A、7或8 B、8 C、8或9 D、106. 如图所示,下列说法中:①与是同旁内角;②与是内错角;③与是内错角;④与是同位角.正确的个数是( )
A、 B、∠1=∠3 C、∠AOD与∠1互为补角 D、∠1的余角等于 75°31'2. 下列语句中,正确的是( )A、相等的角一定为对顶角 B、不是对顶角的角一定不相等 C、不相等的角一定不是对顶角 D、有公共顶点且和为的两个角一定为邻补角3. 已知A、B、C三点,若过其中任意两点画一条直线,则画出的不同直线( )A、一定有三条 B、只能有一条 C、可能有三条,也可能只有一条 D、以上结论都不对4. 如果同一平面内有三条直线,那么它们交点个数是( )个.A、3个 B、1或3个 C、1或2或3个 D、0或1或2或3个5. 若平面内互不重合的4条直线只有3个交点,则平面被分成了( )个部分.A、7或8 B、8 C、8或9 D、106. 如图所示,下列说法中:①与是同旁内角;②与是内错角;③与是内错角;④与是同位角.正确的个数是( ) A、1个 B、2个 C、3个 D、4个7. 下列图形中, 由∠1=∠2, 能得到AB∥CD的是( )A、
A、1个 B、2个 C、3个 D、4个7. 下列图形中, 由∠1=∠2, 能得到AB∥CD的是( )A、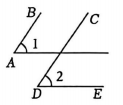 B、
B、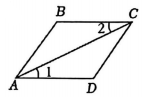 C、
C、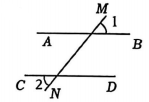 D、
D、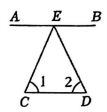 8. 如图,某条行车路线共拐了三次弯,最后行车路线与开始的路线是平行的.已知第一次转过的角度为120°,第三次转过的角度为135°,则第二次转过的角度为( )
8. 如图,某条行车路线共拐了三次弯,最后行车路线与开始的路线是平行的.已知第一次转过的角度为120°,第三次转过的角度为135°,则第二次转过的角度为( ) A、75° B、60° C、135° D、120°9. 图1 是视觉错觉艺术风格的作品,这种设计利用背景线条、图案的干扰,制造出视觉认知偏差的冲突,具有很强的趣味性与迷惑性.如图2,现将其中的一组背景线条与直线a,b抽象出来,下列说法能判断出的是( )
A、75° B、60° C、135° D、120°9. 图1 是视觉错觉艺术风格的作品,这种设计利用背景线条、图案的干扰,制造出视觉认知偏差的冲突,具有很强的趣味性与迷惑性.如图2,现将其中的一组背景线条与直线a,b抽象出来,下列说法能判断出的是( ) A、 B、 C、 D、10. 如图,已知AM∥BN , ∠A=64°,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN , 分别交射线AM于点C、D , 下列结论:①∠ACB=∠CBN;②∠CBD=58°;③当∠ACB=∠ABD时,∠ABC=29°;④当点P运动时,∠APB∶∠ADB=2∶1的数量关系不变.其中正确结论有( )个
A、 B、 C、 D、10. 如图,已知AM∥BN , ∠A=64°,点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN , 分别交射线AM于点C、D , 下列结论:①∠ACB=∠CBN;②∠CBD=58°;③当∠ACB=∠ABD时,∠ABC=29°;④当点P运动时,∠APB∶∠ADB=2∶1的数量关系不变.其中正确结论有( )个 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题:本大题共5小题,每小题4分,共20分
-
11. 如图,直线、相交于点O,射线平分 , . 若 , 则的度数为 .
 12. 如图,有下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角.其中正确的是.(写序号)
12. 如图,有下列结论:①∠2与∠3是内错角;②∠2与∠B是同位角;③∠A与∠B是同旁内角;④∠A与∠ACB不是同旁内角.其中正确的是.(写序号) 13. 如图,在直线a外有一点P,经过点P可以画无数条直线,如果 ,那么过点P的其它直线与直线a一定不平行,理由是 .
13. 如图,在直线a外有一点P,经过点P可以画无数条直线,如果 ,那么过点P的其它直线与直线a一定不平行,理由是 .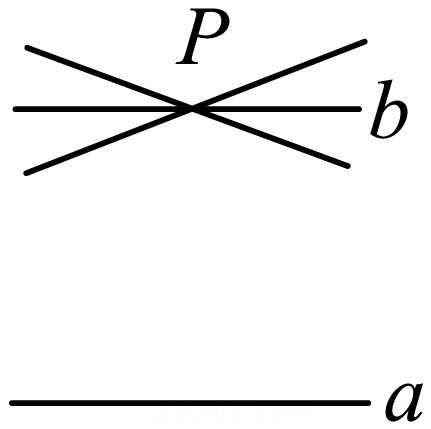 14. 如图,直线 , 点E , F分别在直线 , 上,点P为直线与间一动点,连接 , , 且 , 的平分线与的平分线交于点Q , 则的度数为 .
14. 如图,直线 , 点E , F分别在直线 , 上,点P为直线与间一动点,连接 , , 且 , 的平分线与的平分线交于点Q , 则的度数为 . 15. 学习了平行线后,小明想出了过直线外一点画这条直线的平行线的方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知小明画平行线的依据可以是.(把所有正确的序号填上)
15. 学习了平行线后,小明想出了过直线外一点画这条直线的平行线的方法,她是通过折一张半透明的纸得到的,如图所示,由操作过程可知小明画平行线的依据可以是.(把所有正确的序号填上)
①同位角相等,两直线平行;
②两直线平行,内错角相等;
③同旁内角互补,两直线平行;
④如果两条直线和第三条直线平行,那么这两条直线平行.
三、解答题:本大题共8小题,共75分
-
16.(1)、在一条直线上有n个点,以这些点为端点的线段共有多少条?(2)、平面内有n 条两两相交直线,这n条直线最少有几个交点?最多有几个交点?17. 如图,已知点A , B表示同一条铁路上的两个火车站,点C表示码头,直线a , b分别表示铁路和河流.按下列要求画图:
 (1)、画出直线a;(2)、从火车站A到码头C怎样走最近,请画图表示;(3)、从码头C到铁路怎样走最近,请画图表示.18. 如图,是内一点,点在上.过点画一条直线平行于 , 过点画一条直线平行于 , 直线交于 .
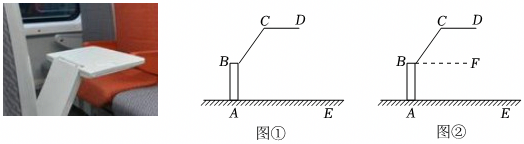
(1)、画出直线a;(2)、从火车站A到码头C怎样走最近,请画图表示;(3)、从码头C到铁路怎样走最近,请画图表示.18. 如图,是内一点,点在上.过点画一条直线平行于 , 过点画一条直线平行于 , 直线交于 .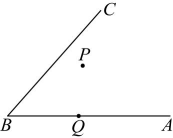 (1)、用直尺和三角尺画平行线的方法,画出图形.(2)、若 , 求的度数.19. 高速列车为了方便乘客放置小件物品,在座椅的后方都安装了可折叠的小桌板,将小桌板放下后,桌面与车厢的底部AE平行,从侧面观察得到如图①所示图形,BA⊥AE , 垂足为A , CD∥AE , 有同学认为在这种情况下,∠ABC与∠BCD的和是个定值,下面是小林同学计算∠ABC+∠BCD的度数的过程,请你将解答过程补充完整.
(1)、用直尺和三角尺画平行线的方法,画出图形.(2)、若 , 求的度数.19. 高速列车为了方便乘客放置小件物品,在座椅的后方都安装了可折叠的小桌板,将小桌板放下后,桌面与车厢的底部AE平行,从侧面观察得到如图①所示图形,BA⊥AE , 垂足为A , CD∥AE , 有同学认为在这种情况下,∠ABC与∠BCD的和是个定值,下面是小林同学计算∠ABC+∠BCD的度数的过程,请你将解答过程补充完整.解:如图②,过点B作BF∥AE ,
因为CD∥AE( ),
所以( )∥CD(平行于同一条直线的两条直线平行),
所以∠BCD+∠CBF=( )°( ),
因为AB⊥AE( ),
所以∠EAB=( )°(垂直定义),
因为BF∥AE ,
所以( )+∠EAB=180°,
所以∠ABF=180°﹣90°=( )°,
所以∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=( )°.
 20. 如图,已知点O 为直线AB 上一点, , OM 平分 , .
20. 如图,已知点O 为直线AB 上一点, , OM 平分 , . (1)、求 的度数.(2)、试说明:OP 平分 .(3)、若改变 的大小,其余条件不变,设 , (2)中的结论是否依然成立? 若成立,请说明理由;若不成立,请用含α的式子表示 .21. 课题学习:平行线问题中的转化思想.
(1)、求 的度数.(2)、试说明:OP 平分 .(3)、若改变 的大小,其余条件不变,设 , (2)中的结论是否依然成立? 若成立,请说明理由;若不成立,请用含α的式子表示 .21. 课题学习:平行线问题中的转化思想.【阅读理解】“两条平行线被第三条直线所截”是平行线中的一个重要的“基本图形”.与平行线有关的角都存在着这个“基本图形”中,且都分布在“第三条直线”的两旁.当发现题目的图形“不完整”时要添加适当的辅助线将其补充完整.将“非基本图形”转化为“基本图形”这体现了转化思想.有这样一道典型问题:
例题:如图(1).已知 , 点在直线、之间,探究与、之间的关系.

解:过点作.
, ,
,
,
,
.
【学以致用】
(1)、如图(1),当 , 时,;(2)、①如图(2),已知 , 若 , , 求出的度数.②如图(3),在①的条件下,若、分别平分和 , 求的度数.
22. 如图①,把一块含角的直角三角尺的边放置于长方形直尺的边上. (1)、填空:______°,______°;(2)、现把三角尺绕点逆时针旋转 .
(1)、填空:______°,______°;(2)、现把三角尺绕点逆时针旋转 .①如图②.当 , 且点恰好落在边上时,求 , 的度数(结果用含的式子表示);
②当时,是否会存在三角尺某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,请直接写出所有的值和对应的那两条垂线;如果不存在,请说明理由.
23. 实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.如图1,一束光线射到平面镜上,被反射后的光线为 , 则入射光线、反射光线与平面镜所夹的锐角 .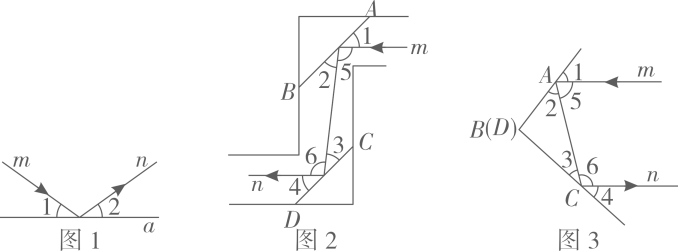 (1)、利用这个规律人们制作了潜望镜,图2是潜望镜的工作原理示意图,AB、CD是平行放置的两面平面镜.已知光线经过平面镜反射时,有 , 请判断入射光线和反射光钱是否平行,并说明理由.(2)、显然,改变两面平面镜AB、CD之间的位置关系、经过两次反射后,入射光线与反射光线之间的位置关系会随之改变,如图3,一束光线射到平面镜AB上,被AB反射到平面镜CD上,又被CD反射.若被CD反射出的光线和光线平行,且 , 则°,°.(3)、试猜想:在图3中,当两平面镜AB,CD的夹角的度数是多少时,可以使任何入射光线经过平面镜AB、CD的两次反射后,与反射光线平行?请说明理由.
(1)、利用这个规律人们制作了潜望镜,图2是潜望镜的工作原理示意图,AB、CD是平行放置的两面平面镜.已知光线经过平面镜反射时,有 , 请判断入射光线和反射光钱是否平行,并说明理由.(2)、显然,改变两面平面镜AB、CD之间的位置关系、经过两次反射后,入射光线与反射光线之间的位置关系会随之改变,如图3,一束光线射到平面镜AB上,被AB反射到平面镜CD上,又被CD反射.若被CD反射出的光线和光线平行,且 , 则°,°.(3)、试猜想:在图3中,当两平面镜AB,CD的夹角的度数是多少时,可以使任何入射光线经过平面镜AB、CD的两次反射后,与反射光线平行?请说明理由.