相关试卷

1、如图是一水压机空心钢立柱的示意图.如果其高h 为 18 m，外径D为1m，内径d 为0.4m ，每立方米钢的质量为7.8t，求该立柱的质量.（π取3.14，结果保留小数点后两位.）

查看解析
2、一张正方形纸片的边长减少 2cm ，它的面积就减少 20 cm² ，这张正方形纸片的边长是多少?

查看解析
3、已知 ${(x + y)}^{2} = 25, {(x - y)}^{2} = 9,$ 求 xy与 $x^{2} + y^{2}$ 的值.

查看解析
4、已知 $m = \frac{1}{2}, n = \frac{3}{5},$ 求代数式（m-2n）（m+2n）+（m+2n）²-4mn的值.

查看解析
5、计算：

(1)、 $4 {(x + 1)}^{2} - 2 (x + 5) (2 x - 10);$

(2)、 $3 {(y - z)}^{2} - (2 y + z) (- z + 2 y);$

(3)、 ${(2 x^{2} + 1)}^{2} - (x + 2) (x^{2} + 4) (x - 2);$

(4)、 $[x (x^{2} y^{2} - x y) - y (x^{2} - x^{3} y)] \div (3 x^{2} y) .$

查看解析
6、先化简，再求值： ${(x + 2 y)}^{2} + (x + y) (x - y) - y^{2},$ 其中x=3， y=2.

查看解析
7、计算：

(1)、 $2 x (x^{2} - 1) - x (x^{2} + 2);$

(2)、 ${[(x - 3) (x + 3)]}^{2} - {(x^{2} + 1)}^{2} .$

查看解析
8、计算：

(1)、 ${(2 a)}^{3} \cdot b^{4} \div (12 a^{3} b^{2});$

(2)、 $(- \frac{2}{3} a^{7} b^{5}) \div (\frac{3}{2} a^{2} b^{5});$

(3)、 $(\frac{6}{5} a^{3} x^{4} - 0.9 a x^{3}) \div (\frac{3}{5} a x^{3});$

(4)、 $(7 x^{2} y^{3} - 8 x^{3} y^{2} z) \div (8 x^{2} y^{2}) .$

查看解析
9、计算：

(1)、 ${(- 2 x^{2} y^{3})}^{2} {(x y)}^{3};$

(2)、（2a+3b）（2a-b）；

(3)、 $5 x^{2} (x + 1) (x - 1);$

(4)、（2x+y-1）²；

(5)、59.8×60.2；

(6)、198².

查看解析
10、计算：

(1)、 $100 \times 1 0^{3} \times 1 0^{2};$

(2)、[（-2）²]³；

(3)、 ${(- x)}^{2} \cdot x^{3};$

(4)、 $x \cdot x^{2} \cdot x^{3} + {(x^{3})}^{2} .$

查看解析
11、如图，直线l₁ ， l₂是两条平行的直线，图形G是一条封闭的曲线.先作图形G关于直线l₁对称的图形，得到图形G₁ ，再作图形G₁关于直线 l₂对称的图形，得到图形G₂.图形G₂可以由图形G平移得到吗?如果可以，平移的方向与直线l₁ ， l₂有什么关系?平移的距离是多少?

查看解析
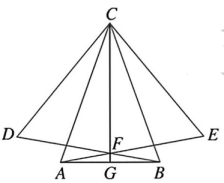
12、如图， △ABC 是等腰三角形， AC=BC，△BCD 和△ACE 是等边三角形， AE与BD 相交于点F，连接CF 并延长，交AB于点G.求证：G为AB的中点.

查看解析
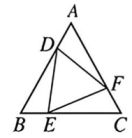
13、如图， △ABC是等边三角形， BD 是中线，延长BC至E，使CE=CD. 求证DB=DE.

查看解析
14、如图，在等边三角形ABC的三边上，分别取点 D， E， F，使AD=BE=CF.求证：△DEF 是等边三角形.

查看解析
15、如图， AD是△ABC的角平分线， DE， DF 分别是 $△ A B D$ 和 $△ A C D$ 的高.求证： AD 垂直平分EF.

查看解析
16、如图，从图形Ⅰ到图形Ⅱ是进行了平移还是轴对称?如果是轴对称，找出对称轴；如果是平移，是怎样的平移?

(1)、

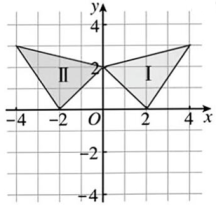(2)、

(3)、

(4)、

查看解析
17、作出下列轴对称图形的对称轴.

查看解析
18、如图，在△ABC中， ∠ACB=90°， CD是高， ∠A=30°. 求证 $B D = \frac{1}{4} A B .$ 综合运用

查看解析
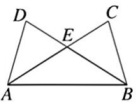
19、如图， AD=BC， AC=BD，求证： △EAB 是等腰三角形.

查看解析
20、如图，在△ABC 中， ∠ABC=50°， ∠ACB=80°，延长CB 至D，使DB=BA，延长BC至E，使CE=CA，连接AD， AE. 求∠D， ∠E， ∠DAE 的度数.

查看解析

上一页 150 151 152 153 154 下一页跳转